Авдеев Е.Ф., Смирнова В.О. Конспект лекций по курсу Механика жидкости и газа eng

MINISTRY OF EDUCATION AND SCIENCE OF THE RUSSIAN FEDERATION FEDERAL STATE AUTONOMOUS EDUCATIONAL INSTITUTION OF HIGHER EDUCATION

"National Research Nuclear University" MEPhI "

Obninsk Institute of Atomic Energy -

branch of the federal state autonomous educational institution of higher education "National Research Nuclear University" MEPhI "

(IATE MEPhI)

Department of Nuclear Physics and Technology

Avdeev E.F., Smirnova V.O.

Abstract

of lectures on the course "Fluid and Gas Mechanics"

Obninsk, 2018

Foreword

The presentation of the material is presented by the deductive method - from the general to the particular.

In order not to obscure the physics of the process, the intermediate mathematical calculations are either partially given or omitted.

The practical orientation of the course for the specialty ―Nuclear power plants: operation, design and engineering‖ or related directions of training graduates has been maintained.

The fifth-year student, Smirnova V.O., whom I deservedly co-authored, provided invaluable assistance in preparing the outline.

Avdeev E.F.

1. Introduction. Axiomatics of fluid and gas mechanics

It is impossible to establish the following disciplines without establishing the main provisions of the MZHG: ―Heat and Mass Transfer‖, ―Steam Generators‖, ―Steam Turbine Installations‖, etc.

The discipline uses a macro approach, which assumes that the final volumes are filled with elementary volumes that completely fill the space, the dimensions of which are small compared with the characteristic sizes of the processes, in terms of the size of the molecules.

The assumption of continuity of the environment is the basis for the choice of the mathematical apparatus of continuous functions. The second assumption is the easy movement of the medium with the absence of a constant component of static friction. The latter defines a special law for stress, which depends on e on the relative deformation of the volume (solids), and on the strain rate.

The introduction of an ideal fluid model (no friction) is a necessary necessity, since in the general case there will be 11 unknowns (including 6 stresses) for a real medium, and the number of equations for determining them is only 6. Introducing an ideal fluid model reduces the number of stresses to one concept of pressure, the number of unknowns (6) is reduced to the number of equations. If the model of an ideal fluid for internal flow problems in channels almost does not give anything (except for gas flow with low viscosity), then for external flow problems it gives almost 100% agreement with experiment. The effect of compressibility due to speed starts at about 2/5 of the speed of sound in the medium.

Compressibility due to speed has an effect, starting from about 2/5 of the speed of sound in the medium, up to these values of the speeds, the regularities in the dropping liquid and gas are the same (if there is no strong influence of pressure and temperature), therefore the term ―liquid‖ can also be understood as dropping liquids and gas: the explanation of many real processes can only be obtained by invoking the characteristics of acoustics (sound velocity) in the medium. Therefore, starting to study the discipline, in addition to mathematical analysis, equations of mathematical physics, thermodynamics, the initial knowledge of the section of oscillation and wave physics is necessary.

2. Basic concepts of kinematics and images of kinematics of a fluid

The value of kinematics is difficult to overestimate, since only from the distribution of velocities can dynamic values (force) be obtained for external flow around bodies and the law of resistance in internal flow problems in the channels.

2.1 The task of movement. Expression for full acceleration

In contrast to the Lagrange method in the MZHG, the method of specifying the motio according to Euler is adopted - by specifying the velocity field at fixed points in space at any time moment t:

move.

From here the full acceleration of a particle, for example along the X axis will be:

(2.2)

where – are called local acceleration, and the other 3 terms - convective acceleration. Further, in the equations of motion will be used to write the full acceleration in the form:

2.2 Line current and tube current. Bulk and massive costs. Average and mass speeds

The current line in the general case differs from the trajectory, although both concepts are characterized by a tangential direction of velocity at their points. However, for the streamline, the speeds at the points are taken at the same moment in time, and the image of the trajectory can be obtained only with the passage of time. For stationary flows, when the direction and magnitude of the velocity do not change, the streamlines and the trajectory will coincide. The condition of the coincidence of the elementary vector of the tangent δr and velocity gives a differential equation for determining the streamline:

If we lead the current lines through an arbitrary closed loop, we obtain a prismatic current surface, the inner region of which is called the current tube. By summing the products of the normal components of the velocity to the elementary platform of the current tube section, the usual flow is obtained Q:

, introduces the concept of average speed. The average speed is easily determined by dividing the flow by the cross section, and the parameters of interest to the engineer try to be expressed in terms of this easily determined value.

Through the side surface of the current tube there can be no flow, by definition ( ), however, the volume flow along the current tube will be unchanged only at constant density. Otherwise, the volume flow varies.

To enter the value that along the current tube will always be constant, the volume flow rate is multiplied by the density and come to an understanding of the mass flow rate G:

It is equated to the product of the mass velocity ρw and the sectional area.

Mass velocity plays an important role in engineering calculations, since it remains constant at constant cross sections.

2.3 The concept of circulation velocity

Through this concept is (Г) the force of resistance of pressure in the problems of external flow around well-streamlined bodies, when the generator of the profile coincides with the streamline usually taken as zero.

The velocity circulation G in the section of an arbitrary current line AB is called the sum of the products of the velocity projection on the direction of the tangent at a given point Vs on the arc element ds:

and the velocity circulation will be equal to the potential difference at point B and point A.

, that is, coincides with the speed potential. The imposition of velocity circulation on symmetrical profiles distorts the symmetry of the velocity distribution and leads to a

non-zero force, its value is associated with the shape of the streamlined body. In the theory of vortices (outside the vortex), it determines the nature of the velocity distribution.

2.4 Vortex lines and vortex tubes. Distribution of velocities and pressures in the section of vortices

The concept of a vortex line is introduced in the same way as current lines, only now the angular velocities ̅ are directed are tangentially directed along this line. The latter means that there is no translational motion of two vortex lines, only rotation around it of elementary volumes. Of course, it can occur when ̅ is parallel to ̅ , but then we will talk about the vortex motion. The concepts of a vortex surface are found similarly to current surfaces. Then the fluid is inside the vortex surface, called the vortex tube. The intensity of the vortex tube i (vortex) is the sum of the products of the normal components of the angular velocity on the elementary area of the vortex cross section dσ, that is, the flow of the vector of angular velocity:

Since the flow of the vector of angular velocity on the side surfaces of the vortex tube is zero ( ), the intensity of the vortex tube is kept constant along it.

It follows from the latter that the vortex tubes cannot end in a liquid. ( ). Since this would lead to infinitely large angular velocities. The latter explains the forms of existence of vortices:

-either closed toroidal;

-or their final sections are on surfaces of very different densities (earth, water surface).

It is necessary to understand that not every rotational (circular) motion is vortex, it is necessary to have instantaneous axes of rotation, that is, vortex lines. Therefore, there are areas within the vortex, where ̅ and areas outside the vortex where ̅ , but circular rotational movements take place. On the basis of the Stokes formula (transition from the integral over the contour to the integral over the surface spanned by this contour), the equality of the intensity of the vortex tube and the velocity circulation along the contour located on its surface is proved. But if the vortex tube is one, the contour does not have to be on its surface, it will still be i = Г. In other cases (two or more vortex tubes), the value of the velocity circulation around the contour covering several vortex tubes may turn out to be zero, which may lead to a false conclusion about the absence of vortex tubes.

Denoting by the vortex radius, and calculate the velocity circulation along the contour of the radius (one vortex tube) we get: , whence the hyperbolic decrease in velocity from the surface of the vortex Va, to zero at infinity:

(2.9)

And inside the vortex there will be a linear decrease in speed from Va to zero in the center of the vortex.

For the integrity of the presentation, we borrow the relationship between pressure and speed from section 4.

Outside the vortex movement without vortex and for any points:

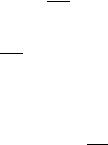
(2.11)

Inside the vortex, the relationship of pressure and peripheral speed is different:

(2.12)

Having determined the constant from the condition on the surface of the vortex and replacing it through the pressure , we obtain the parabolic law of pressure reduction when approaching the center of the vortex.

(2.13)

In the center of the vortex (V=0) pressure will be lower than ambient pressure by Knowledge of the above is useful not only for operators of industrial reactors, since a

large-radius vortex in the lower manifold would lead to a local decrease in pressure drops in fuel assemblies above the vortex and a decrease in their consumption. And if it is in the upper collector - to increase costs. Vortices always exist, but in industrial reactors the lower collector has a perforated elliptical bottom that breaks large vortices into small ones, on the surface of which V_a is small, small and transverse pressure gradient. In the upper reservoir, the large vortices are real. This is useful to know and experimenters, leading research on a group of simulators FA.

If there are two whirlwinds, then, depending on the direction of their twist, they will move as a pair whirlwind or in parallel, causing a ―dance‖ of expenses on the fuel assembly.

3. Mathematical representation of the law of conservation of mass and its consequences

3.1. Continuity equation

The preservation of the mass flow rate of a fluid (possibly a two-phase one) is already an integral representation of the law of conservation of mass.

The differential equation is obtained by equating to zero the time derivative of the mass of the elementary volume and replacing the rate of change of the relative volume with the velocity divergence:

It becomes possible to set (or not compressibility) of a fluid in the velocity field, since according to (3.1), at

volume flow.

Stall currents accompanied by discharge and cavitation destruction of the wall material occurs when the wall shape does not coincide with the current line.

es:

(3.6)

The relationship between the potential of the velocity and the current function (3.6) coincides with the Cauchy-Riemann conditions, which are necessary for the existence of the function

function of the flow, since, if its expression is known, all kinematic quantities can be found (streamlines, velocity, flow rate and velocity circulation):

∫̅

3.3.Peculiarities of turbulent flow kinematics. Critical Reynolds Number

These features are just the fundamental reason for the absence of a rational theory of turbulence. Unlike laminar flows, in turbulent velocity flows and other parameters pulsate at the same point, which leads to the uncertainty of the boundary conditions for solving the NavierStokes equations. To eliminate this cause, Reynolds proposed to introduce averaged parameters, for example, for speed ̅ , where – ripple speed. Substituting the averaged velocities and pressures into the Navier-Stokes equation solved the problem of defining boundary conditions, but led to another problem — the uncertainties of the terms containing the parameter pulsations. The latter is solved only at the level of hypotheses, the validity of which is verified by experiments.

For a century, it was not possible to determine the criterion by which it is necessary to establish the flow regime - it is laminar or turbulent. This could not be done even D.I. Mendeleev, who purposefully, on behalf of the government, dealt with this problem.

And only the Englishman Reynolds proposed to determine the flow regime according to the totality of parameters - viscosity, velocity and geometric size.

Initially, Reynolds indicated the incorrect critical value of his criterion. This is not surprising, since the transition to a turbulent flow actually occurs in the range (

) Now generally accepted for pipes, the critical number

4. Mathematical representation of the law of conservation of momentum. Integral D. Bernoulli and the Bernoulli equation for a flow of a final section

4.1. Classification of forces acting in a fluid

In an easily deformable liquid medium (water), forces are classified into mass and surface. Mass forces are given by mass distribution density vector:

one hand, is the force when the volume is tightened to a point. The vector of mass force is singlevalued at each point, therefore it forms a vector field. An example of mass forces of conservative fields would be gravity, inertial forces, forces of electrodynamic origin, if the fluid is charged.

For further we define the potentials of mass forces, in the case of the action of the forces

The projections of the force ̅ on the axis will be related to the potential U by dependen-

cies:

And the full differential dU can be written through the projections of the force:

(4.4) If we assume that the z axis is directed upwards, and when both gravitational forces act

simultaneously and there is rotation around the z axis with an angular velocity ̅:

However the vectors ̅ do not form a vector field, since at each point there will be a set of values ̅depending on the platform orientation. This is a consequence of the non−isotropy of the real environment. There is a problem in determining the voltage at the point. You can express (using the principle of dalamber) vector ̅ through the stresses on mutually orthogonal plat-

Here, the indices of the stress vectors mean directions to the pads:

In the projections on the axis (4.8) gives three scalar equalities:

That is, the state at a point will be determined by 9 voltages, which, in combination, are called the stress tensor.

For Newtonian fluids (absence of static friction), a linear relationship between the stress

where – tensor unit.

Relationship (4.9) is also called the generalized "law" of Newton, where the coefficient ( – dynamic viscosity) put to get Newton's formula for friction stress in laminar flows, a