5. Извлечение корня из комплексных чисел в тригонометрической форме

Определения и утверждения к 3.1.8 можно найти в [1, с. 191-192].

Комплексное число называется корнемn-й степени из комплексного числаz, если.

Утверждение. При любом натуральномn > 1 и любом комплексномz существует ровноnразличных чисел, таких, что:

(1.4)

где k= 0, 1, 2, ...,n– 1.

Пример 25 Вычислить.

Решение. Для того чтобы воспользоваться формулой (1.4), необходимо представить число, стоящее под знаком корня, в тригонометрической форме. Для числаz = ‑1 найдем его модуль и аргумент:,. В итоге.

По формуле (1.4) . Тогда:

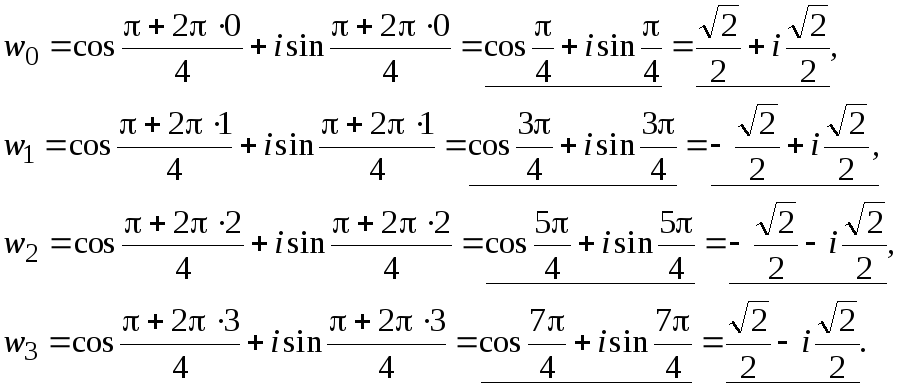
Пример 26 Вычислить .

Решение. Для числа найдем его модульи аргумент:,, так как число лежит на отрицательной части мнимой оси. В итоге. По формуле (1.4), гдеk= 0, 1, 2, 3, 4. Тогда:

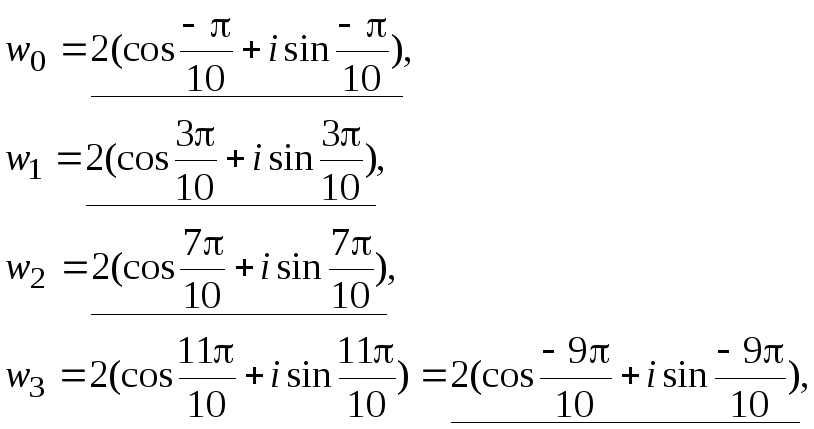
Для иаргументами будути, а неисоответственно, так как.

Пример 27 Вычислить.

Решение. Для числамодульи аргументесть:=,.

В итоге =. По формуле (1.4)

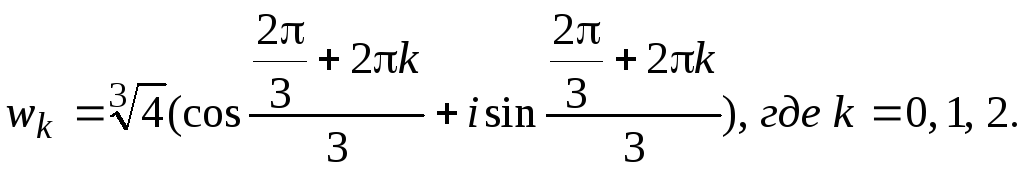Тогда:

И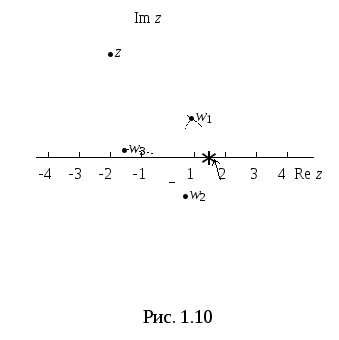з формулы (1.4) видно, что аргументы корнейотличаются на одну и ту же величину, а модули всех корней одинаковые и равны. Значит, на комплексной плоскости всележат на окружности с центром в начале координат и радиусомна одинаковом расстоянии друг от друга. Для примера 27 изображения самого числаи его корней,,можно видеть на рис. 1.10.

2. Многочлены

   1. Многочлены и действия над ними

Определения и утверждения к 2.1 можно найти в [1, с. 203-206].

Для действительной переменной x функция вида, гдеa иx –действительные числа, аn – натуральное число или 0 (по-другому это можно записать как), называется одночленом с действительным коэффициентом.

Многочлен ‑ это сумма одночленов, т.е. функция вида

. При этомназывается старшим коэффициентом и,‑ свободным членом,n ‑ степенью многочлена.

Многочлен тождественно равен 0 тогда и только тогда, когда все его коэффициенты равны 0.

Если в записи многочлена нет какой-либо степени неизвестного, это значит, что коэффициент при этой степени равен 0.

На множестве многочленов определены следующие действия:

1. Сложение.

Пример 28. Найти.

2. Умножение.

Пример 29. Найти.

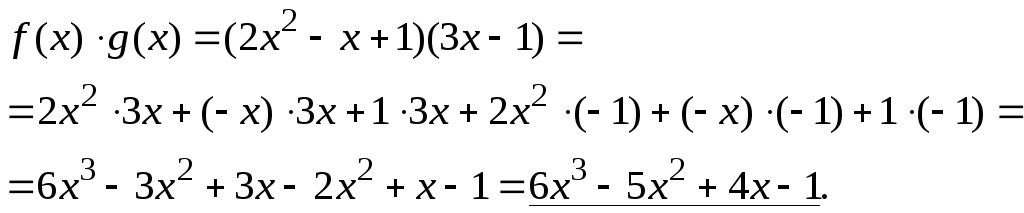
3. Деление с остатком.

Разделить на‑ значит записатьв виде, или. Последняя запись аналогична записи для чисел:, или 17 = 53 + 2.

Теорема (о делении с остатком) [1, с. 206]. Для любых многочленовисуществуют, и притом единственные, многочленыи, такие, что

. (2.1) При этом степеньменьше степени,‑ неполное частное,‑ остаток. Разделитьна‑ значит записатьв виде (2.1).

Для практического нахождения частного и остатка существует метод деления «уголком».

Пример 30 Выполнить «уголком» деление с остатком:

=на =.

Решение.Запишем делимое и делитель как при делении многозначных чисел:

Находим частное от деления старшего члена делимого на старший член делителя () и записываем результат в графу частного:

x

Умножаем делитель на результат деления и записываем под делимым:

x

Вычитаем из делимого результат умножения:

x

Проверяем степень получившегося в результате вычитания многочлена. Если она меньше степени делителя, то процесс деления закончен, и полученный многочлен является остатком. В противном случае деление продолжается аналогично описанному ранее:

x ‑ 1

‑ 4x

Так как степень полученного многочлена меньше степени делителя, то процесс деления закончен. В результате: = x– 1– неполное частное, а

= –4x – остаток.

Ответ: , или

.

Пример 31 Выполнить деление с остатком:на.

Решение. Запишем делимое и делитель как при делении многозначных чисел. Если в записи многочлена отсутствует одна или несколько степеней, то при записи, для удобства вычислений, следует на их места записать нули:

3x +1

Получившиеся в результате умножения многочлены удобнее записывать, располагая слагаемые в соответствии с их степенями. Так как степень полученного многочлена меньше степени делителя, то процесс деления закончен. В результате: =– неполное частное, а= 3x + 1 – остаток.

Ответ:, или.

Пример 32 Делится ли нацело многочленна многочлен?

Решение. Разделим один многочлен на другой «уголком».

0 В остатке от деления получился нуль, значит,многочлен делится на многочленнацелои возможны записи:

, или.