31. Приближенное нахождение суммы числового ряда.

Существуют два основных способа вычислять сумму сходящихся числовых рядов с заданной точностью (в зависимости от использованного признака сходимости).

1. Признак Коши.

1Определим К.

2Выберем q.

3Возьмем минимальное Для любогоn

4Определим минимальное m (натуральное), чтобы

5Возьмем

Сумма n0 членов даст сумму ряда с точностью

2. Признак Даламбера.

1Определим D.

2Выберем q.

3Возьмем минимальное Для любого

4Определим минимальное m (натуральное), чтобы

5Возьмем

Сумма n0 членов даст сумму ряда с точностью

P.S. В методическом пособии по курсу «мат. анализ» рассмотрены только эти 2 способа.

35. Разложение функций в ряд Тэйлора.

Формула Тэйлора выглядит следующим образом:

Для разложения какой-либо функции находятся последовательные производные и подставляются в известную формулу.

Отметим также, что каково бы ни было х, остаточный член при

Пример.

Находим последовательные производные.

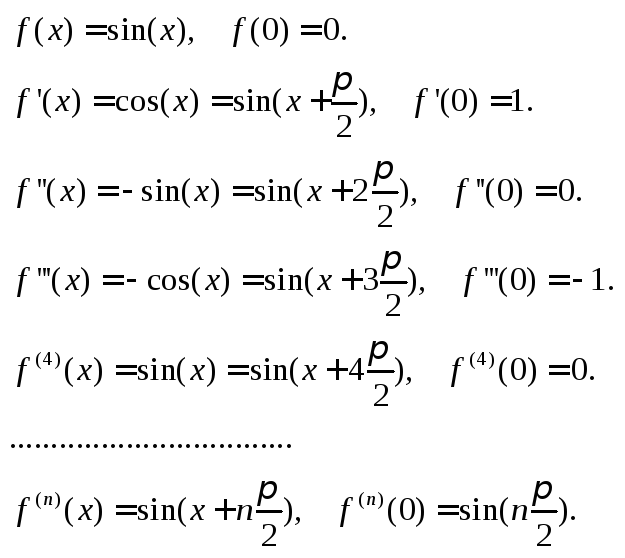
Подставляя значения, получаем:

36. Ряд Тэйлора для функций

1.

Находим последовательные производные.

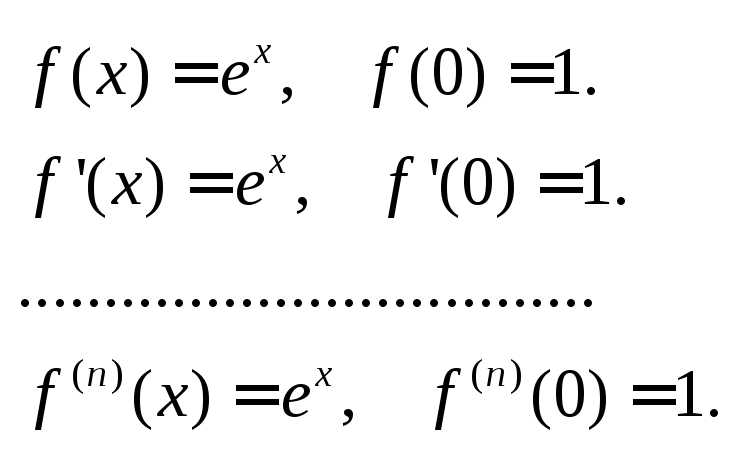
Подставляя выражения в формулу Тэйлора получаем:

Таким образом, взяв достаточное число членов, мы можем вычислить значение функции с любой степенью точности.

2.

Находим последовательные производные.

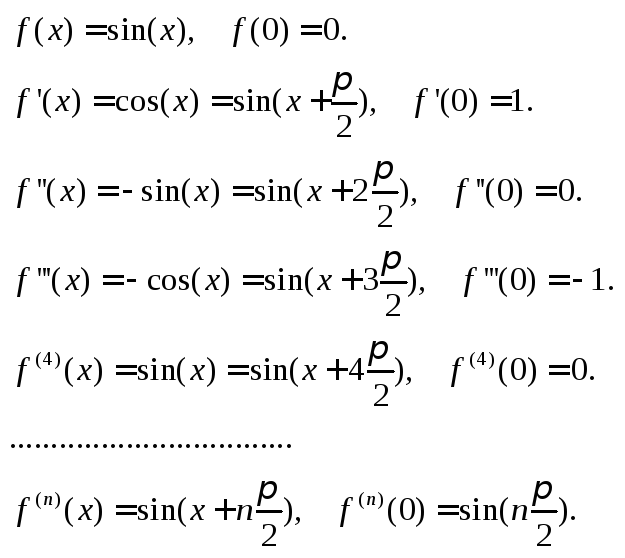
Подставляя значения, получаем:

3.

Аналогично разложению синуса, получаем:

37. Ряд Тэйлора для функций

1.

m – произвольное постоянное число.

Здесь оценка остаточного члена представляет некоторые трудности. Поэтому применим несколько другой способ, нежели для разложения функций синуса и косинуса.

Заметим, что удовлетворяет дифференциальному уравнениюи условию

Найдем степенной ряд, сумма которого удовлетворяет уравнению и условию.

Приравняем коэффициенты при одинаковых степенях х в разных частях равенства:

Для коэффициентов получаем выражения:

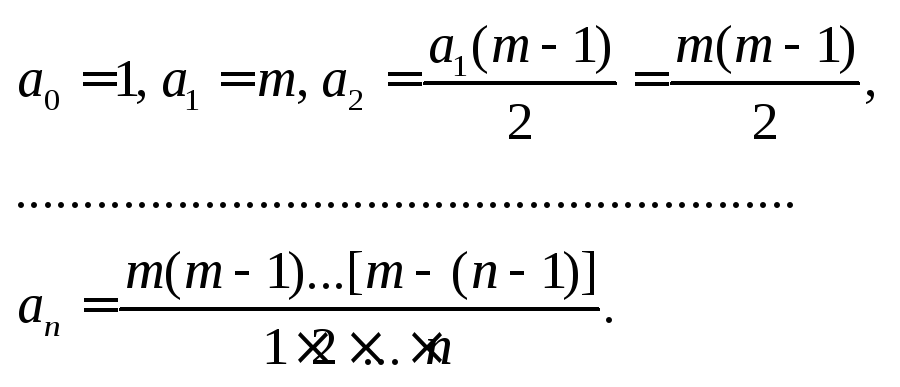
Получаем итоговую формулу:

Если m – целое положительное число, то начиная с определенного члена, все коэффициенты равны нулю и ряд превращается в многочлен.

Если m – дробное или целое отрицательное, имеем бесконечный ряд.

2.

Интегрируя равенство в пределах от 0 до х, получаем:

или

Это равенство справедливо в интервале

Выведем формулу для выведения натуральных логарифмов любых целых чисел.

Положим, что

Тогда

Полагаяполучаем

Итак, подставляя разные значения n, получаем натуральные логарифмы любых чисел.

Пример.

38. Решение дифференциальных уравнений с помощью рядов. Функция Бесселя.

Пусть требуется найти решение дифференц.уравнения 2го порядка удовлетворяющее начальным условиям . Допустим, что решение у=f(x) существует и представимо в виде ряда Тейлора :

Нам нужно найти , т.е. значения производных от частного решения при.

Дифференцируя обе части первоначального уравнения по х получаем: и подставляя значениев правую часть, найдем:

и приx=x0.

Для тех значений х, для которых этот ряд сходится, он представляет решение уравнения.

Уравнение Бесселя.

УБ - дифференциальное уравнение вида:

Решение этого уравнения, следует искать не в форме степенного ряда, а в виде произведения некоторой степени х на степенной ряд:

Перепишем выражение в виде и найдем его производные:

Приравняв коэффициенты при х, получаем систему уравнений. Решив ее, находим при

Поэтому

Общее решение уравнения

функция Бесселя первого рода р-го порядка, решение у1,умноженное на некоторую константу.

функция Бесселя первого рода р-го порядка, решение у2,умноженное на некоторую константу.

При целом положительном бесселева функция определяется, как

Частное решение ищется в форме

Это есть функции Бесселя второго рода n-го порядка.