Переходные процессы в ЛЭЦ 2014

Свободная составляющая не зависит от напряжения на входе цепи и запи-

сывается так же, как в предыдущих задачах:

Принужденные составляющие по форме совпадают с формой приложенного напряжения. Следовательно, принужденная составляющая тока – сину-

соидальная функция времени и ее удобнее всего рассчитывать комплексным методом:

где z 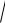R2 2L2 – модуль комплексного сопротивления;

arctg L – аргумент комплексного сопротивления, представляющий со-

R

бой угол сдвига фаз между напряжением u и током i;

Мгновенное значение принужденной составляющей

iпр Jm Im прej t Jm Im прej ej t

Величина i(0+) определяется на основании первого правила коммутации:

так как до коммутации ток был равен нулю.

Следовательно,

20

откуда

Ток в цепи

График функции i(t) представлен на рис. 11.

Если коммутация происходит при , то начальное значение свобод-

2

i

Рис. 11. Зависимость тока от времени в переходном режиме при α = 90º

Если же коммутация происходит при = 0, то в цепи сразу наступает ус-

тановившийся режим без переходного процесса.

Сравнение расчетов переходного процесса при постоянном (2.2.1) и сину-

соидальном (2.2.4) напряжении показывает, что методика расчета одна и та же,

различие состоит в определении токов установившихся режимов до и после коммутации.

21

2.2.5.Включение цепи R, C на синусоидальное напряжение

Вмомент времени t = 0 цепь, состоящая из сопротивления R и

емкости С (рис. 12), включается на синусоидальное напряжение

u Um sin t .

22

Принужденную составляющую целесообразно рассчитывать комплекс-

ным методом:

Мгновенное значение принужденной составляющей напряжения на ем-

Постоянная В определяется по уравнению:

1 t

при t = 0+

Величина uC 0 определяется на основании второго правила комму-

тации:

23

Следовательно,

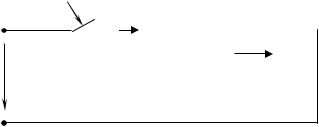
График функции uC t представлен на рис. 13.

Если коммутация происходит при , то начальное значение свобод-

2

ной составляющей напряжения на емкости uC св 0 максимально, а именно

uC св 0 UCmпр , и переходное напряжение достигает экстремального значения в

конце первого полупериода (см. рис.13).

Если же коммутация происходит при = 0, то в цепи сразу наступает ус-

тановившийся режим без переходного процесса.

uC

UCm пр sin ψ

uC пр

uC св

–UCm пр sin ψ

uC

Рис. 13. Зависимость напряжения на емкости от времени в переходном режиме при ψ = 90º

24

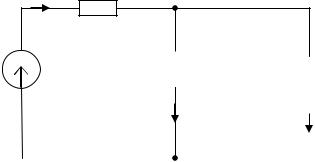
2.2.6. Расчет переходного процесса в разветвленной цепи с индуктивностью при воздействии постоянной ЭДС

Условие задачи: определить токи i1, i2, i3 и напряжение на индук-

тивности после замыкания ключа в схеме, представленной на рис. 14.

Исходные параметры: R1 = 10 Ом; R2 = 10 Ом; R3 = 10 Ом; Е = 100 В;

L = 0,1 Гн.

Расчет переходного процесса складывается из отдельных этапов, которые являются типичными при использовании классического метода для электри-

ческих цепей любой топологии и сложности.

1. Установившийся режим до коммутации. Имеет место установив-

шийся режим постоянных токов (рис. 15). При этом ветвь с током i3 разомкну-

та, поэтому I3 = 0 и схема содержит только один контур. Для определения зна-

чений токов и других представляющих интерес величин на данном этапе при-

меняется один из известных способов расчета цепей постоянного тока. Чаще

всего для этой цели используются законы Кирхгофа.

b

Рис. 15. Схема для расчета Рис. 14. Расчетная схема установившегося режима

до коммутации В рассматриваемом случае по второму закону Кирхгофа

25

откуда

По полученным значениям далее записываем:

i1 0 I1 5A;

(82)

i2 0 I2 5A.

2. Дифференциальные уравнения описывают токи и напряжения с мо-

мента t 0 и чаще всего записываются по законам Кирхгофа:

Решение этой системы для каждой неизвестной, как и ранее, представ-

ляется в форме:

i1 i1пр i1св;

i2 i2 пр i2 св;

(84)

i3 i3пр i3св;

uL uL пр uL св,

где i1пр, i2 пр ,i3пр, uL пр – принужденные составляющие;

i1св, i2 св, i3св, uL св – свободные составляющие.

3. Принужденные составляющие определяются из рассмотрения уста-

новившегося режима, наступающего после переходного процесса (рис. 16).

По законам Кирхгофа записывается система алгебраических уравнений:

26

или

i1пр i2 пр i3пр 0;

10i1пр 10i2 пр 100; (86)

10i2 пр 10i3пр 0.

b

Рис. 16. Схема для расчета установившегося режима после коммутации

Решение системы (86) дает такие результаты:

Принужденная составляющая напряжения на индуктивности определяет-

ся согласно выражению:

так как i2пр= const.

4. Свободные составляющие. Сначала необходимо получить характерис-

тическое уравнение и найти его корни. Для этого существует несколько путей:

а) непосредственное преобразование системы дифференциальных урав-

нений (83) к уравнению относительно одной неизвестной;

б) через определитель коэффициентов системы (83);

в) по входному сопротивлению схемы.

27

Наиболее удобными являются два последних способа, поэтому остано-

вимся только на них.

Получение характеристического уравнения через определитель сис-

темы дифференциальных уравнений. Вводя замену р ddt, переписываем систему (83) в виде:

По левой части уравнений (88) составляем определитель коэффициентов

Приравнивая последний к нулю, получаем характеристическое уравнение

p 150c 1.

Получение характеристического уравнения через входное сопротив-

ление. Здесь используется аналогия с комплексным сопротивлением.

Входное комплексное сопротивление схемы (см. рис. 14) для послеком-

мутационного состояния

Заменяя j на р и приравнивая полученный результат к нулю, получаем:

28

Легко убедиться в том, что преобразование соотношения (93) приводит к характеристическому уравнению (90).

Так как характеристическое уравнение имеет единственный корень, то свободные составляющие записываются в следующей форме:

5. Определение постоянных. В результате расчета мы получили сле-

дующие выражения для неизвестных:

i1 i1 пр i1 св 6,67 A1 e 150 t;

i2 i2 пр i2 св 3,33 A2 e 150 t;

(95)

i3 i3 пр i3 св 3,33 A3 e 150 t;

uL uL пр uL св A4 e 150 t.

Чтобы определить неизвестные постоянные А1, А2, А3, А4, необходимо сначала вычислить начальные значения i1 0 , i2 0 , i3 0 и uL 0 . Пос-

ледние определяются как решение системы алгебраических уравнений, полу-

чаемых из системы дифференциальных уравнений (83), записываемой при t 0 в виде:

По первому правилу коммутации i2 0 i2 0 5. Перенося это зна-

чение в правую часть уравнений (96), получаем систему

i1 0 i3 0 5;

с тремя неизвестными i1 0 , i3 0 и uL 0 в левой части. Решение систе-

мы (97) дает такие результаты:

29