Практическое занятие № 1:

Расчет на прочность и жесткость при линейном растяжении-сжатии

Задача № 1: расчет на прочность и жесткость круглого стержня

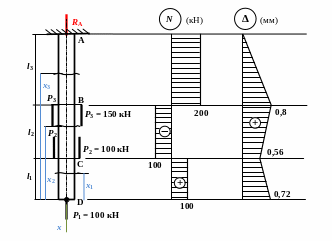
Эта задача может быть решена без определения реакции опоры. Однако в данном примере реакция будет найдена. Расчет же эпюры крутящего момента выполним в последовательности, когда величина реакции в вычислениях не используется. В задаче задано: размеры стержня l₁ = 0,4 м; l₂ = 0,6 м; l₃ = 1 м; нагрузки сосредоточенная сила Р₁ = 100 кН; две симметричные силы Р₂ = 100 кН; две симметричные силы Р₃ = 150 кН; материал – сталь ст.3, для которой [] = 160 МПа; Е = 2 · 10⁸ кПа.

Требуется подобрать сечение стержня из условия прочности, рассчитать деформации стержня.

1. Р асчет опорной реакции: из условия равновесия имеем

2. Расчет и построение эпюры N

В любой последовательности рассматриваем нагрузочные участки стержня после его рассечения. В рассматриваемом примере на всех участках рассматриваются нижние отсеченные части стержня, отмеченные соответствующей координатой х. При этом внутренняя сила N определялась как алгебраическая сумма всех внешних сил, действующих вдоль оси стержня на выбранной отсеченной части. Внешняя сила записывалась со знаком плюс, если растягивала рассматриваемую часть стержня.

Участок СD:

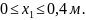
Н а этом участке расчет продольной силы с использованием метода сечений выполним подробнее. Рассекая стержень в произвольном сечении и выбирая для расчета нижнюю часть (верхняя часть в этом случае отбрасывается), получаем расчетную схему, показанную ниже на рисунке.

На схеме ось х выбрана по оси стержня перпендикулярно сечению. Предполагаемая внутренняя сила N₁

в сечении направлена в принятом положительном направлении (действует на растяжение стержня).

Расстояние показывает положение сечения относительно точки D. Равновесие при неподвижности рассматриваемой отсеченной части записывается уравнением:

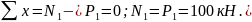
Для остальных участков схема отсеченной части не рисуется, а получается на выше приведенной схеме всего стержня закрытием листом бумаги верхней отбрасываемой части. Уравнение равновесия не записывается, а значение внутренней силы N определяется алгебраической суммой всех внешних сил, действующих вдоль оси стержня на выбранной отсеченной части.

Участок ВС:

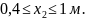
N₂ = Р₁ – 2Р₂ = 100 – 2 · 100 = – 100 кН.

Участок АВ:

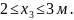
N₃ = Р₁ – 2Р₂ + 2 · 150 = 100 – 2 · 100 + 2 · 150 = 200 кН.

Так как во всех трех выражениях для продольной внутренней силы произвольная координата сечения отсутствует, их графики на всех трех участках эпюры представляют собой постоянные значения (эпюра построена правее схемы стержня). Проверка построенной эпюры выполняется по скачкообразным изменениям (на жаргоне математиков – скачкам функции) значения внутреннего усилия в сечении. Такие скачки эпюре N всегда должны быть в сечении, где на оси стержня приложена внешняя сосредоточенная сила: скачек равен этой силе. Такие скачки на эпюре можно видеть в сечении D (100 кН), где на стержне приложена сосредоточенная сила Р₁ = 100 кН, в сечении С (200 кН), где на стержне приложены две силы Р₂, в сечении В (300 кН), где на стержне приложены две силы Р_3. В сечении А на эпюре N можно видеть скачек величиной 200 кН. Этот скачек строго соответствует действующей в этом сечении опорной реакции R_A. При этом в расчетных выражениях для продольной силы опорная реакция отсутствует (т.к. в расчетах всегда выбирались нижние отсеченные части стержня, где опорной реакции нет). Это совпадение говорит о правильности построения эпюры.

3. Расчет на прочность стержня

По условию рассматриваемой задачи заданный стержень имеет постоянное сечение по всей длине. Следовательно, материал такого стержня будет нагружен наиболее сильно в пределах нагрузочного участка АВ: 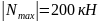. Запишем условие прочности:

Предполагая полную загрузку материала (в выше приведенном выражении знак неравенства заменяется на знак равенства), получаем уравнение с одним неизвестным. Определяем требуемое (минимально допустимое) значение площади сечения:

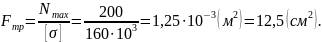
Т.к. 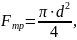диаметр стержня должен быть не менее

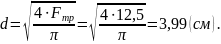
4. Расчет деформаций стержня

В сечении А стержень имеет заделку. Следовательно, это сечение неподвижно: Δ_А = 0. Сечение В стержня по отношению к сечению А опустится вниз за счет удлинения части стержня АВ при растяжении. Последнее определяется по закону Гука при растяжении:

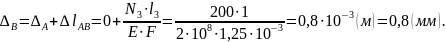
Далее аналогично:

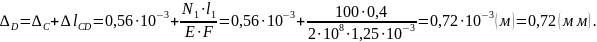
По полученным значениям строим правее эпюры эпюру деформаций заданного стержня при растяжении-сжатии. Графики изменения деформаций линейны, т.к. в соответствии с законом Гука продольная деформация пропорциональна длине стержня.

Задача № 2: расчет стержня на прочность и жесткость при сложном нагружении

В задаче задано: размеры стержня l₁ = 1 м; l₂ = 0,6 м; l₃ = 0,4 м.

Нагрузки: сосредоточенные силы Р₂ = 20 кН; Р₃ = 40 кН;

распределенные нагрузки q₁ = 10 кН/м; q₃ = 30 кН/м.

Материал – сталь ст.3, для которой [] = 160 МПа; Е = 2 · 10⁸ кПа.

Нагрузочные участки АВ и ВС круглого сечения; участок CD – квадратного сечения. Схема нагружения представлена ниже. ВС и СD – круглое сечение, АВ – квадратное.

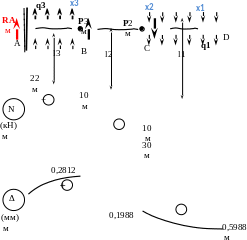
Из предыдущей задачи следует, что расчет стержня с заделкой можно выполнить без определения реакции опоры. Ее величину получим по построенной эпюре N.

1. Расчет и построение эпюры N

Т.к. реакция опоры R_A не определена, будем на всех нагрузочных участках рассматривать правую отсеченную часть (на схеме стержня показаны соответствующими координатами сечений х₁, х₂, х₃).

Участок АВ:

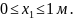
N₁ = – q₁ · х₁. Получили линейную зависимость от х₁. Рассчитываем две точки эпюры N:

при х₁ = 0 м N₁ = – 10 · 0 = 0 кН;

при х₁ = 1 м N₁ = – 10 · 1 = – 10 кН.

Участок ВС:

N₂ = – q₁ · l₁ – Р₂ = – 10 · 1 – 20 = – 30 кН.

Участок АВ:

N₃ = – q₁ · l₁ – Р₂ + Р₃ + q₃ · (х₃ – l₁ – l₂ ). Рассчитываем две точки эпюры N:

при х₃ = 1,6 м N₃ = – 10 · 1 – 20 + 40 + 30 · (1,6 – 1 – 0,6 ) = 10 кН;

при х₁ = 2 м N₃ = – 10 · 1 – 20 + 40 + 30 · (2 – 1 – 0,6 ) = 22 кН.

Проверка эпюры показывает, что все скачки значения N соответствуют действующим внешним сосредоточенным силам. Скачек на эпюре в сечении А показывает, что реактивный момент R_А = 22 кНм.

2. Расчет на прочность стержня

Конструкция расчетного стержня на показанной схеме его нагружения показывает, что следует рассчитать площадь сечения на каждом нагрузочном участке.

Участок АВ: по эпюре N видим, что здесь опасное сечение в точке В. . Запишем условие прочности:

Тогда требуемое значение площади сечения:

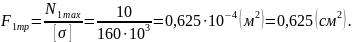
Если часть стержня на АВ выполнить с квадратным сечением, то 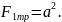Тогда сторона квадратного сечения должна быть

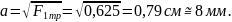
Участок ВС: здесь во всех сечениях 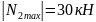. В соответствии с условием прочности получаем:

Если часть стержня на ВC выполнить круглого сечения, то диаметр стержня должен быть не менее

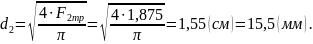
Участок СD: здесь наибольшее нагружение материала происходит в сечении А 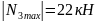. В соответствии с условием прочности получаем:

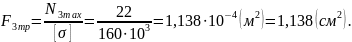
Если часть стержня на ВC выполнить круглого сечения, то диаметр стержня должен быть не менее

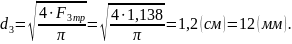
3. Расчет деформаций стержня

Сначала рассмотрим методику определения продольной деформации стержня, находящегося под продольной распределенной нагрузкой (эта методика на лекции не рассматривалась). Такой нагрузкой в частности является собственный вес стержня, расположенного вертикально (см. ниже приведенный рисунок)

Для правого стержня в показанном сечении (рассматривается нижняя отсеченная часть) получаем внутреннее усилие: N = q · x₁. Это линейная зависимость от координаты. В результате имеем при x₁ = 0 N = 0, а при x₁ = l N = q·l. Эпюра имеет вид треугольника.

Эквивалентной действию собственного веса стержня можно считать нагружение сосредоточенной силой P = q·l в центре тяжести стержня (на расстоянии l/2 от любого из его концов). При подстановке указанной силы и указанного расстояния в формулу закона Гука для деформации получаем:

Эквивалентной действию собственного веса стержня можно считать также нагружение всего стержня сосредоточенной силой, равной среднему значению силы N по приведенной эпюр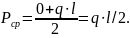е: Расчетное значение продольной деформации получим тоже:

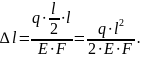
Т.о., любая из предложенных методик может быть использовании для расчете продольной деформации от распределенной нагрузки. Отмети, что график деформаций здесь будет парабола, причем вершина параболы всегда находится в сечении, где N = 0.

Переходим к рассматриваемой задаче. В сечении А стержень имеет заделку. Следовательно, это сечение неподвижно: Δ_А = 0. Сечение В стержня по отношению к сечению А опустится вниз за счет удлинения части стержня АВ при растяжении. Последнее определяется по закону Гука при растяжении:

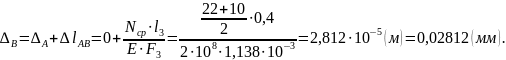
Можно рассчитать продольное удлинение участка АВ еще одним способом – как сумму постоянной и переменной составляющих продольной силы N:

На участке CD действует только распределенная нагрузка q₁, подобно собственному весу стержня. Ее направление таково, что эта часть стержня сжимается. В результате имеем:

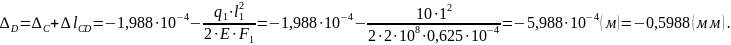
График изменения деформаций линейный только на участке, где продольная сила постоянна. На участках АВ и CD зависимости продольных деформаций параболические. Т.к. точный график деформаций в данной задаче не требуется, эти зависимости построены приблизительно так, чтобы в сечении, где построенная эпюра N на участке должна стать равной нулю.

А.В. Климович