
Задачи Крюкова / Кинетика 11
.docxЗадача 1
1. При взаимодействии эквивалентных количеств моноксида углерода и хлора по уравнению:
СО + Cl2 → COCl2
при 300 К в присутствии катализатора наблюдалось следующее уменьшение общего давления системы:
t, мин |
0 |
5 |
10 |
15 |
21 |
р·10-5, Па |
0.965 |
0.900 |
0.829 |
0.779 |
0.735 |
Определите порядок реакции (V = const).
Решение:
Воспользуемся аналитическим вариантом метода подбора, рассчитаем константы скорости для каждого времени по следующим уравнениям:
По уравнению Менделеева – Клапейрона:
pV=nRT , следовательно С=p/RT
k=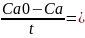
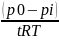 - для реакции
0-го порядка
- для реакции
0-го порядка
k=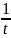 ln
ln =
ln
=
ln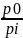 – для
реакции 1-го порядка
– для
реакции 1-го порядка
k=
 =
=
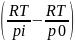 – для реакции 2-го
порядка
– для реакции 2-го
порядка
k=
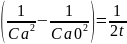
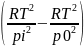 - для реакции 3-го порядка
- для реакции 3-го порядка
Рассмотрим
данную реакцию. Так как даны эквивалентные
количества CO
и Cl2, то
 0=
P(Cl2) 0 = P0/2
= 0,965 *10^5 /2 = 0,4825 *10^5
0=
P(Cl2) 0 = P0/2
= 0,965 *10^5 /2 = 0,4825 *10^5
Запишем
давление в момент времени
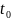 и t:
и t:
|
CO |
Cl2 |
COCL2 |
t=0 |
|
/2 |
0 |
t |
( /2)-x |
( /2)-x |
x |
Общее давление системы будет равно:
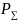 =
P(CO)+P(Cl2)+P(COCl2)= 2
=
P(CO)+P(Cl2)+P(COCl2)= 2 /2-x)+x=
-x
/2-x)+x=
-x
x= -
=
P(Cl2)=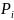 =
(
/2)-x=
/2-(
-
)=(
/2)-
+
=
-(
/2)
=
(
/2)-x=
/2-(
-
)=(
/2)-
+
=
-(
/2)
·10^-5, Па |
0,4825 |
0,4175 |
0,3465 |
0,2965 |
0,2525 |
t,мин |
0 |
5 |
10 |
15 |
21 |
P |
48250 |
48247,3927 |
48244,54 |
48242,54 |
48240,77 |
lnP |
10,78415111 |
10,63945473 |
10,45305 |
10,29722 |
10,13658 |
1/P |
2,07254*10^-5 |
0,059712575 |
0,071948 |
0,084081 |
0,098733 |
1/P^2 |
4,29542*10^-10 |
0,003565592 |
0,005177 |
0,00707 |
0,009748 |
|
|
k1 |
k2 |
k3 |
k4 |
для 0 порядка |
k0 |
0,521460088 |
0,545527477 |
0,497393 |
0,439325 |
для 1 порядка |
k1 |
0,028939275 |
0,03310981 |
0,032462 |
0,030837 |
для 2 порядка |
k2 |
0,01193837 |
0,007192733 |
0,005604 |
0,004701 |
для 3 порядка |
k3 |
0,000356559 |
0,000258826 |
0,000236 |
0,000232 |
Из полученных значений констант можно сделать вывод о том, что наиболее вероятный порядок реакции – первый.
Построим зависимости для подтверждения вывода, воспользовавшись интегральным методом подбора кинетического уравнения:
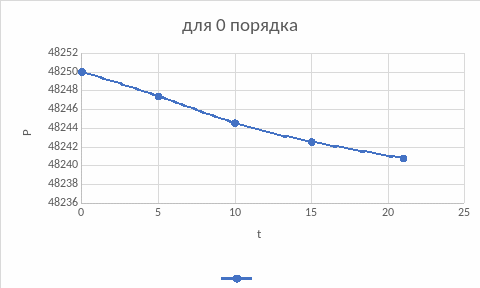
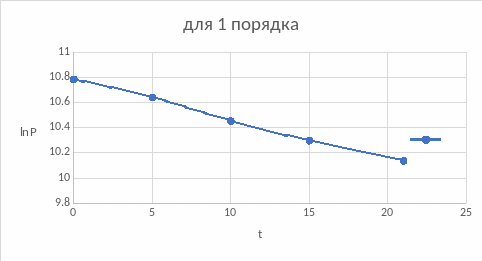
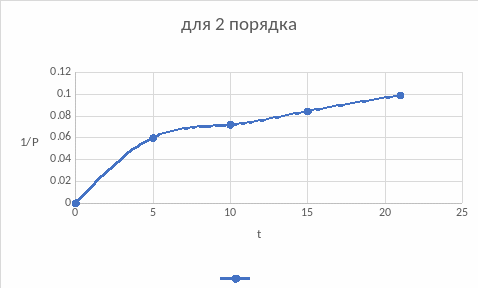
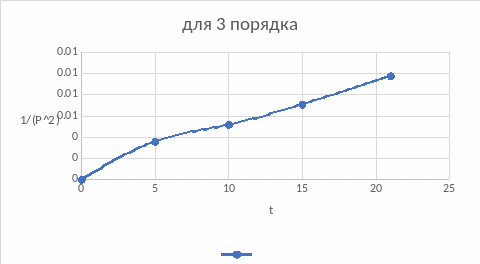
По графикам также подходит первый порядок, нулевой подходит меньше, если сравнивать значения констант обоих порядков.
Ответ: 1 порядок (расчеты и графики в файле Excel: «1 задача»)
Задача 2
Реакция С6Н5N(CH3)2 + CH3I → С6Н5N(CH3)3+ + I–
характеризуется
единичными частными порядками по каждому
из реагентов. При проведении реакции в
нитробензоле (растворитель) при 24.8 оС
константа скорости составляет 8.39·10-5
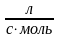 .
Рассчитайте время, через которое
израсходуется 75% С6Н5N(CH3)2,
если начальные концентрации реагентов
были равны и составляли 0.1 моль/л.
.
Рассчитайте время, через которое
израсходуется 75% С6Н5N(CH3)2,
если начальные концентрации реагентов
были равны и составляли 0.1 моль/л.
Решение:
Обозначим концентрации реагентов как:
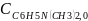 =
= =
=
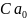
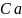 =
=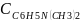
Так как частные порядки реагентов единичные, а общий порядок реакции равен сумме частных порядков, то:
n
=
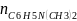 +
+
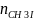 =
1+1=2
=
1+1=2
r=
k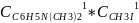
Запишем кинетическое уравнение реакции второго порядка в интегральной форме:
kt=
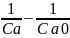 (1)
(1)
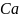 =
=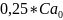 (так как израсходовалось 75% С6Н5N(CH3)2
). (2)
(так как израсходовалось 75% С6Н5N(CH3)2
). (2)
Подставим (2) в (1):
kt=
 =
=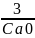
t=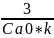 =357569 с
=357569 с
Ответ : t=357569 с
Задача 3
Две реакции одинакового порядка имеют равные предэкспоненциальные множители, но их энергии активации различаются на 41.9 кДж/моль. Рассчитайте соотношение скоростей этих реакций при 600 К.
Решение:
Рассмотрим уравнение Аррениуса в экспоненциальной форме для констант двух реакций:
k1=A*exp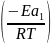
k2=A*exp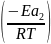
Пусть
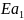 = x
(Дж/моль) , тогда
= x
(Дж/моль) , тогда
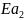 = x+41900
(Дж/моль)
= x+41900
(Дж/моль)
Так как даны реакции одинакового порядка, то соотношение их скоростей можно представить как соотношение констант этих реакций:
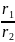 =
=
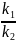 =
=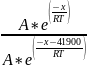 =
=
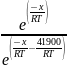 =
=
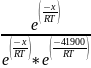 =
=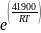 =
=
= 4462,8
Ответ: =4462,8


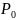 /2
/2