Добавил:

nikinator25 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский технический университет связи и информатики

Предмет:

Вычислительная математика

Файл:

Лабораторные (заочн)

.pdf

Скачиваний:

Добавлен:

15.02.2021

Размер:

1.54 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

5.3. Варианты задания

Таблица 5-1

№	Уравнение
вар	y' = x y2
1
2	y' = y2 (x2+ x + 1)
3	y' = x3 y2
4	y' = y / cos2(x)
5	y' = y cos(x)
6	y' = y2cos(x)
7	y' = x2 y + y
8	y' = (x – 1)2 y2
9	y' = x3 y
10	y' = y2 sin(x)
11	y' = y sin(x)
12	y' = x y
13	y' = y2 / x
14	y' = x2 y
15	y' = y2 (2 – x)
16	y' = 3 x2 y2
17	y' = y2 (ex + 4x)
18	y' = y (x – 1)
19	y' = x (1 + y2)
20	y' = x / (2y)
21	y' = y / (3 x2)
22	y' = 4 x e-3y
23	y' = 2 x y
24	y' = 2 x (y1/2)
25	y' = y2 ex
26	y' = x (1 – y2)1/2
27	y' = (1 + x) y
28	y' = x2 (1 – y2)1/2
29	y' = (x2 + x) y2
30	y' = y2 / cos2(x)
31	y' = y2sin x
32	y' = cos(x) y
33	y' = 2x y
34	y' = (x-1)2 y2
35	y' =	y2 cos(x)
36	y' = 0.5 y2
37	y' = y2 x
38	y' =	xy
39	y' = y2 ex
40	y' = e-y

0	-2	0.4
0	-2	0.2
0	-2	0.2
0	1	0.1
0	1	0.5
0	-1	0.4
0	1	0.2
0	-1	0.5
0	1	0.2
0	0.5	0.2
0	1	0.4
0	1	0.2
1	1	0.2
0	1	0.2
0	-1	0.4
0	-4	0.2
0	-1	0.4
0	1	0.4
0	0	0.2
0	1	0.4
1	1	0.2
1	0	0.2
0	1	0.2
0	1	0.4
0	-2	0.4
0	0	0.4
0	1	0.2
0	0	0.4
0	-1	0.4
0	-1	0.3
0	1	0.1
0	1	0.1
0	1	0.1
0	1	0.1
0	-1	0.1
1	1	0.1
0	-2	0.1
3	3	0.1
1	-1	0.1
1	0	0.1

a
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
3
1
1

4
2
2
1
5
4
2
5
2
2
4
2
2
2
4
2
4
4
1.6
4
3
3
2
4
4
1.6
2
1.6
4
1.5
1
1
1
1
1
2
1
4
2
2

Тема1.5.Методы решенияОДУ (Лабораторный практикум)

Страница 2

5.4. Содержание отчета

1.Индивидуальное задание.

2.Решение ОДУ аналитическим методом.

3.Значения полученного аналитического решения y(x) на отрезке [a;b] с шагом h,

4.«Ручной расчет» численного решения ОДУ методом Эйлера – функция ye(x) в первых 4-х точках заданного отрезка [a;b] с шагом h и оценка погрешностей полученного решения по методу двойного просчета (правилу Рунге).

5.Значения численного решения ОДУ, вычисленные методом Эйлера – функция y1(x) во всех точках заданногоотрезка [a;b] с шагом h, используя математический пакет.

6.Значения численного решения ОДУ, вычисленные методом Рунге-Кутты 2 порядка –

функция y2(x) во всех точках заданного отрезка [a;b] с шагом h, используя математический пакет.

7.Значения численного решения ОДУ, вычисленные методом Рунге-Кутты 4 порядка –

функция y4(x) во всех точках заданного отрезка [a;b] с шагом h, используя математический пакет.

8.Вычисленные значения погрешностей численного решения дифференциального уравнения для каждого метода.

9.Графическая иллюстрация полученных решений.

5.5.Пример выполнения задания

1.Задание для численного решения обыкновенных дифференциальных уравнений:

дифференциальное уравнение y' 2yx ;

интервал [1;6];

начальные условия x0=1, y0=1;

шаг интегрирования h=0.5.

2.Точное аналитическое решение заданного дифференциального уравнения

Найдем точное аналитическое решение заданного дифференциального уравнения y(x)

методом разделения переменных. dydx 2yx

Запишем уравнение в виде ydy 2xdx и проинтегрируем обе части равенства с учетом начальных условий.

ydy	y2	;	2xdx x2
	2

2y2 x2 c

Из начальных условий найдем константу c: 12 1 с, следовательно с 12

y 2x2 2c 2x2 1

Таким	образом, аналитическое (точное) решение дифференциального	уравнения
y(x)
	2x2 1	Страница 3
Тема1.5.Методы решенияОДУ (Лабораторный практикум)

3. Значения точного решения ОДУ – y(x)

Вычислим значения полученного решения y(xi), где i 0,1,...,n, n bha на отрезке [1;6] с шагом изменения аргумента h=0.5:

y(x) 2x2 1

x 1 1.5 6

y(x)

1.51.87083

22.64575

2.53.39116

34.12311

3.54.84768

45.56776

4.56.2849

5.57.71362

68.42615

4.«Ручной расчет» численного решения ОДУ методом Эйлера и оценка погрешностей полученного решения по методу двойного просчета.

Выполним «ручной расчет» численного решения ОДУ методом Эйлера. Найдем значения

численного решения ОДУ методом Эйлера (функцию ye(x)) в первых 4-х точках заданного отрезка [1;6] с шагом h=0.5, т.е. на отрезке [1;3].

Для этого ОДУ записывают в виде y’=f(x,y).

Рекуррентная формула для определения очередного значения функции по методу Эйлера имеет вид: yi+1=yi+h f(xi,yi), где i 0,1,...,n, n bha .

Таким образом, в нашем случае формула расчета имеет вид: yei 1 yei h f (xi, yei ), где i=0,1,2,3,4. Очередное значение аргумента функции рассчитывается по формуле xi 1 xi h. Решение:

Задано ОДУ y' 2yx , сначальными условиями x0=1, y0=1 и шагоминтегрирования h=0.5.

Т.е.	f (x, y) 2x . Расчет 4-х точек решения ОДУ методом Эйлера:
		y
ye	ye	h f (x	0	, ye ) 1 0.5		2 1	2,		x x		0	h 1 0.5 1.5
ye	ye	h f (x		, ye ) 1 0.5			2,		x x			h 1 0.5 1.5
1	0			0		1			1
						1
ye	ye	h f (x , ye ) 2 0.5			2 1.5			2.75,		x		2	x		h 1.5 0.5 2
ye	ye	h f (x , ye ) 2 0.5						2.75,		x			x		h 1.5 0.5 2
2	1	1		1		2								1
						2
ye	ye	h f (x	2	, ye ) 2.75 0.5			2 2		3.477			,	x	3	x	2	h 2 0.5 2.5
ye	ye	h f (x		, ye ) 2.75 0.5					3.477			,	x		x		h 2 0.5 2.5
3	2			2			2.75
							2.75

Тема1.5.Методы решенияОДУ (Лабораторный практикум)

Страница 4

ye	ye	h f (x	, ye ) 3.477 0.5	2 2.5	4.196	, x	4	x	3	h 2.5 0.5 3

4	3	3	3	3.477

Таким образом, численное решение ОДУ методом Эйлера есть табличная функция ye(x):

x ye(x)

1 1

1.52

2 2.75

2.5 3.477

3 4.196

Формула для оценки погрешности решения ОДУ методами Рунге-Кутты имеет следующий вид:

R	yi(h)	yi(h/2)
	yi(h)	yi(h/2)

	2p 1
	2p 1

где p – порядок метода Рунге-Кутты. При этом в каждой точке хi по формуле, соответствующей методу, производится расчет yi с шагом h (yi(h)) и с шагом h/2 (yi(h/2)).

Расчет по приведенной формуле называется методом двойного просчета или правилом

Рунге.

Выполним оценку погрешностей полученного методом Эйлера решения ОДУ по этому правилу. Для этого необходимо решить ОДУ с шагом h/2=0.25.

y' 2yx , сначальными условиями x0=1, y0=1 и шагом интегрирования h=0.25

ye1 1 0.25		2 1				1.5			x1=1.25

		1							x2=1.5

ye2 1.5 0.25			2 1.25				1.917

				1.5

ye3 1.917	0.25				2 1.5			2.308	x3=1.75

					1.917

ye4 2.308	0.25				2 1.75			2.687	x4=2

					2.308
ye5 2.687	0.25					2 2		3.059	x5=2.25

				2.687
ye6 3.059	0.25				2 2.25			3.427	x6=2.5

					3.059
ye7 3.427	0.25				2 2.5			3.792	x7=2.75

					3.427

ye8 3.792	0.25				2 2.75			4.155	x8=3

					3.792

Тема1.5.Методы решенияОДУ (Лабораторный практикум)

Страница 5

Оценим погрешность решения ОДУ методом Эйлера (или методом Рунге-Кутты 1 порядка,

где p=1) по формуле:R

втаблицу:

1.25

1.5

1.75

2.25

2.5

2.75

yi(h) yi(h/2)

21 1

ye(x)(h)

2.75

3.477

4.196

yi(h) yi(h/2) для каждой точки и сведем вычисления

ye(x)(h/2)	R
1
1.5
1.917	0.083
2.308
2.687	0.063
3.059
3.427	0.05
3.792
4.155	0.041

5.Численное решение ОДУ методом Эйлера с использованием Mathcad

Найдем значения численного решения ОДУ методом Эйлера (функцию y1(x)) во всех

точках заданного отрезка [1;6] с шагом h=0.5, используя математический пакет Mathcad:

Решение методом Эйлера (Рунге-Кутты 1 порядка) - ф-ция y1:

f(x y)	2 x	h 0.5	n 10	i 0 n	1
	y

					x			1
Начальные условия:					0			1
				y1				1
						0
Формулы для расчета:
xi 1				xi h
				h f x y1
y1		y1	i	h f x y1
	i 1		i	i			i

Вывод всей таблицы-решения:
i	0 n
xi		y1i

1 1

1.52

2 2.75

2.53.47727

3 4.19623

3.54.91115

4 5.62382

4.56.33508

5 7.04541

5.5 7.75509

6 8.4643

				Страница 6
Тема1.5.Методы решенияОДУ (Лабораторный практикум)				Страница 6

6. Численное решение ОДУ методом Рунге-Кутты 2 порядка с использованием

Mathcad

Найдем значения численного решение ОДУ методом Рунге-Кутты 2 порядка (функцию y2(x)) во всех точках заданного отрезка [1;6] с шагом h=0.5, используя математический пакет Mathcad, по расчетной формуле метода Рунге-Кутты 2-го порядка:

h f(x,y

) f(x

h,y

hf(x,y

)) ,

i 1

i i

где

i 0,1,2,...,n 1.

Решение методом Рунге-Кутты 2 порядка - функция y2:

f(x y)

2 x

h 0.5

n 10

0 n

Начальные условия:

y20

Формулы для расчета:

xi 1

xi h

y2i 1

f x y2

f x

h y2

f x

Вывод всей таблицы-решения:

0 n

y2i

1 1

1.51.875

2 2.64883

2.53.39358

3 4.1251

3.54.84938

4 5.56924

4.5 6.28621

5 7.00118

5.57.71469

68.42713

7.Численное решение ОДУ методом Рунге-Кутты 4 порядка с использованием

Mathcad

Расчетная формула метода Рунге-Кутты 4-го порядка имеет вид: yi 1 yi h6(k1 2k2 2k3 k4 ),

где

k1	f(xi,yi);
k2	f(xi h/2,yi hk1 /2);
k3	f(xi h/2,yi hk2 /2);
k4	f(xi h,yi hk3).	Страница 7
Тема1.5.Методы решенияОДУ (Лабораторный практикум)		Страница 7

ВMathcad для численного решения ОДУ методом Рунге-Кутты 4-го порядка

предназначена функция rkfixed(y, x0, xend, N, D), где y – первоначально равно y0,

x0 и xend – начальное и конечное значения аргумента,

N – количество проводимых вычислений решения(точек таблицы), D - это выражение для вычисления правой части уравнения, т.е. f(x,y).

Результатом вычислений функции rkfixed( ) служит матрица из N+1 строк и 2-х столбцов.

Впервом столбце этой матрицы содержатся координаты узлов x0, x1, x2 … xend, а во втором

– значения приближенного решения в соответствующих узлах.

Найдем значения численного решение ОДУ методом Рунге-Кутты 4 порядка (функцию y4(x))

во всех точках заданного отрезка [1;6] с шагом h=0.5, используя математический пакет

Mathcad:

Решение методом Рунге-Кутты 4 порядка средствами Mathcad :

нач. значение: y0 1

ОДУ: f(x y) 2x y0

Решение для y на отрезке от 1 до 6 из 10 точек - это матрица (табличная функция) Y:

Y rkfixed(y 1 6 10 f)

		0		1

	0		1	1
	1		1.5	1.87137

	2		2	2.64615

	3		2.5	3.39147
Y	4		3	4.12336
Y	5		3.5	4.8479
	5		3.5	4.8479

	6		4	5.56795

	7		4.5	6.28507

	8		5	7.00015

	9		5.5	7.71376

	10		6	8.42627

Для удобства и дальнейших расчетов погрешностей полученного решения дифференциального уравнения правый столбец матрицы Y(т.е. столбец с номером 1) присваивается переменной y4.

Тема1.5.Методы решенияОДУ (Лабораторный практикум)

Страница 8

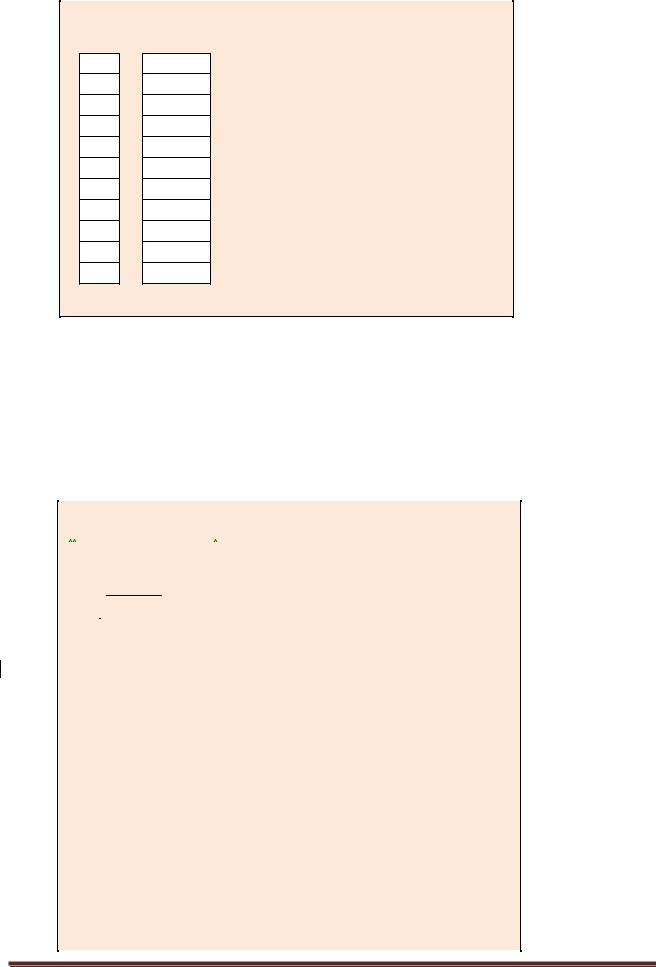
	y4 Y1	i 0n
	xi	y4i

1 1

1.51.87137

2 2.64615

2.53.39147

3 4.12336

3.54.8479

4 5.56795

4.56.28507

5 7.00015

5.57.71376

68.42627

8.Значения погрешностей численного решения дифференциального уравнения для каждого метода

Для сравнения выведем все полученные разными методами решения

дифференциального уравнения и вычислим значения погрешностей каждого метода как разность между аналитическим (точным) решением и соответствующим численным решением в каждой точке табличной функции.

yti - аналитическое решение ОДУ, y1i - решение ОДУ, полученное методом Эйлера, y2i - решение ОДУ методом Рунге-Кутты 2-го порядка, y4i - решение ОДУ методом Рунге-Кутты 4-го порядка


	n 10	i 0n	x0 1	h 0.5	xi 1	xi h

Запишем аналитическое(точное) решение ОДУ как дискретную функцию yti

yti 2 xi 2 1

Полученные решения:


	xi	yti	y1i	y2i	y4i
	1	1	1	1		1
	1.5	1.87083	2	1.875		1.87137

	2	2.64575	2.75	2.64883		2.64615

	2.5	3.39116	3.47727	3.39358		3.39147

	3	4.12311	4.19623	4.1251		4.12336

	3.5	4.84768	4.91115	4.84938		4.8479

	4	5.56776	5.62382	5.56924		5.56795

	4.5	6.2849	6.33508	6.28621		6.28507

	5	7	7.04541	7.00118		7.00015

	5.5	7.71362	7.75509	7.71469		7.71376

	6	8.42615	8.4643	8.42713		8.42627
							Страница 9

Тема1.5.Методы решенияОДУ (Лабораторный практикум)

Погрешности:			y1i			y2i			y4i
		yti	y1i		yti	y2i		yti	y4i
				0			0		0
			0.12917			4.171·10-3			5.459·10-4
			0.10425			3.08·10-3			3.949·10-4
			0.08611			2.42·10-3			3.089·10-4
			0.07312			1.993·10-3			2.542·10-4
			0.06348			1.697·10-3			2.162·10-4
			0.05605			1.477·10-3			1.882·10-4
			0.05018			1.309·10-3			1.668·10-4
			0.04541			1.175·10-3			1.497·10-4
			0.04147			1.067·10-3			1.359·10-4
			0.03815			9.765·10-4			1.244·10-4
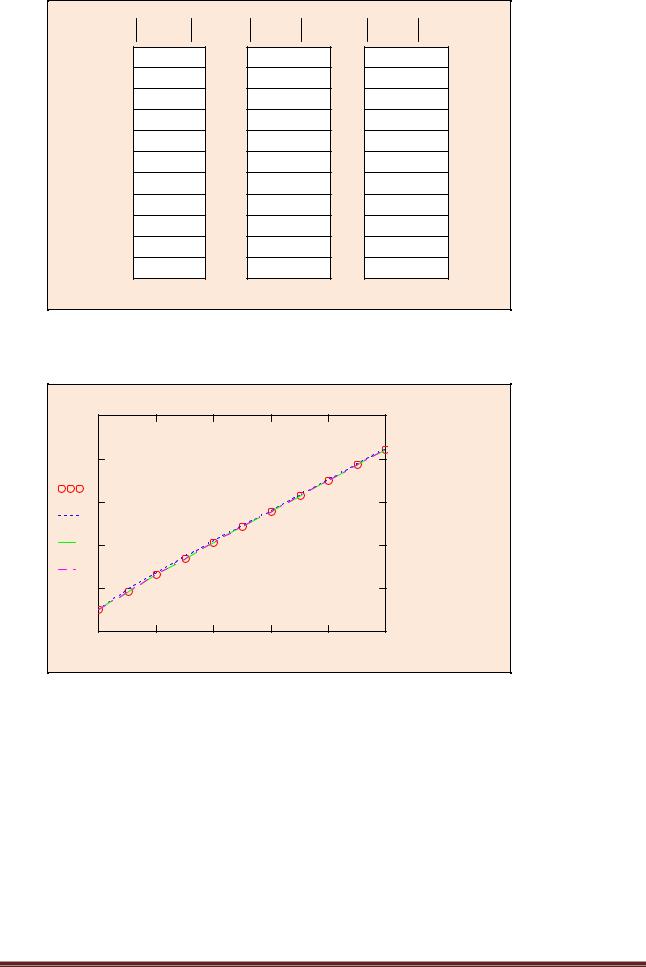
9. Графическая иллюстрация решений
	10
yti	8
yti
y1i	6
y2i	4
y4i	4
	2
	0	1	2	3		4	5		6
					xi
В данном случае все численные решения ОДУ весьма близки к точному решению.

Тема1.5.Методы решенияОДУ (Лабораторный практикум)

Страница 10

5.6. Контрольные вопросы по теме Методы решения дифференциальных уравнений

1.Что такое обыкновенное дифференциальное уравнение?

2.Что такое порядок ОДУ?

3.Что называется аналитическим решением ОДУ 1-го порядка?

4.Что является общим решением ОДУy f(x,y)?

5.Что является геометрической интерпретацией общего решения ОДУy f(x,y)?

6.Что является частным решением ОДУy f(x,y)?

7.Что является численным решением ОДУy f(x,y)?

8.Что относится к начальным условиям при решении ОДУ 1-го порядка численными методами?

9.Имеет ли задача Коши для дифференциального уравнения 1-го порядка единственное решение?

10.По какому правилу проводят оценкупогрешности решения методов Рунге-Кутты?

11.Как выглядит формула для определения очередного значения функции по методу Рунге-Кутты 1-го порядка?

12.Уменьшение шага интегрирования при использовании методов Рунге-Кутты приводит

куменьшению или увеличению погрешности?

13.В обыкновенном дифференциальном уравнении присутствуют производные разных порядков от одной переменной или только первая производная от нескольких переменных?

14.Методы Рунге-Кутты являются одношаговыми или двухшаговыми методами?

15.Сколько раз на каждом шаге необходимо вычислять y(x,y) в модифицированном методе Эйлера?

16.Очередная точка решения ОДУ методом Рунге-Кутты вычисляется на основании одного или двух предыдущих значений функции?

17.Возможно ли в методах Рунге-Кутты применение переменного шага интегрирования?

18.Процесс решения дифференциального уравнения называется интегрированием или дифференцированием?

19.Каковы формулы оценки погрешности методов Рунге-Кутты?

20.Почему метод Эйлера называют методом Рунге-Кутты первого порядка?

21.Модифицированный метод Эйлера иначе называется методом Рунге-Кутты решения ОДУ 1-го или 2-го порядка?

22.Что требуется предварительно сделать, чтобы применить методы Рунге-Кутты при решении ОДУ 2-го порядка?

23.С помощью какого параметра происходит достижение заданной точности решения ОДУ в методе автоматического выбора шага?

24.Можно ли оценить погрешность решения ОДУ, не зная точного решения?

25.В каком методе решения ОДУ подынтегральная функция на отрезке аппроксимируется интерполяционным многочленом 1-го порядка, а затем интегрируется методом прямоугольников?

26.В каком методе решения ОДУ подынтегральная функция на отрезке [xi;xi+1] аппроксимируется интерполяционным многочленом 1-го порядка, а затем интегрируется методом трапеции?

27.Что является начальными условиями ОДУ n-го порядка (для n=2)?

28.Сколько ОДУ 1-го порядка будет содержать система, построенная для решения n-го порядка?

Тема1.5.Методы решенияОДУ (Лабораторный практикум)

Страница 11

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

0	-2	0.4
0	-2	0.2
0	-2	0.2
0	1	0.1
0	1	0.5
0	-1	0.4
0	1	0.2
0	-1	0.5
0	1	0.2
0	0.5	0.2
0	1	0.4
0	1	0.2
1	1	0.2
0	1	0.2
0	-1	0.4
0	-4	0.2
0	-1	0.4
0	1	0.4
0	0	0.2
0	1	0.4
1	1	0.2
1	0	0.2
0	1	0.2
0	1	0.4
0	-2	0.4
0	0	0.4
0	1	0.2
0	0	0.4
0	-1	0.4
0	-1	0.3
0	1	0.1
0	1	0.1
0	1	0.1
0	1	0.1
0	-1	0.1
1	1	0.1
0	-2	0.1
3	3	0.1
1	-1	0.1
1	0	0.1

0	-2	0.4
0	-2	0.2
0	-2	0.2
0	1	0.1
0	1	0.5
0	-1	0.4
0	1	0.2
0	-1	0.5
0	1	0.2
0	0.5	0.2
0	1	0.4
0	1	0.2
1	1	0.2
0	1	0.2
0	-1	0.4
0	-4	0.2
0	-1	0.4
0	1	0.4
0	0	0.2
0	1	0.4
1	1	0.2
1	0	0.2
0	1	0.2
0	1	0.4
0	-2	0.4
0	0	0.4
0	1	0.2
0	0	0.4
0	-1	0.4
0	-1	0.3
0	1	0.1
0	1	0.1
0	1	0.1
0	1	0.1
0	-1	0.1
1	1	0.1
0	-2	0.1
3	3	0.1
1	-1	0.1
1	0	0.1

0	-2	0.4
0	-2	0.2
0	-2	0.2
0	1	0.1
0	1	0.5
0	-1	0.4
0	1	0.2
0	-1	0.5
0	1	0.2
0	0.5	0.2
0	1	0.4
0	1	0.2
1	1	0.2
0	1	0.2
0	-1	0.4
0	-4	0.2
0	-1	0.4
0	1	0.4
0	0	0.2
0	1	0.4
1	1	0.2
1	0	0.2
0	1	0.2
0	1	0.4
0	-2	0.4
0	0	0.4
0	1	0.2
0	0	0.4
0	-1	0.4
0	-1	0.3
0	1	0.1
0	1	0.1
0	1	0.1
0	1	0.1
0	-1	0.1
1	1	0.1
0	-2	0.1
3	3	0.1
1	-1	0.1
1	0	0.1