
Интерполяция по в с е м узлам (многочлен 4 степени):
n 4 i 0 n j 0 n
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
|
|
xx xj |
|
||
|
|
|
|
|
|
|
|
|
|
|
f(xx) |
|
yi if |
i |
|
j 1 |
x |
x |
|
|
|
|
i 0 |
|
j 0 |
|
|
|
i |
j |
|
|
|
|
|
|
|
|
|
||||
f (5) 19.671 |
|
|
|
|
|
|
|
|
|
|
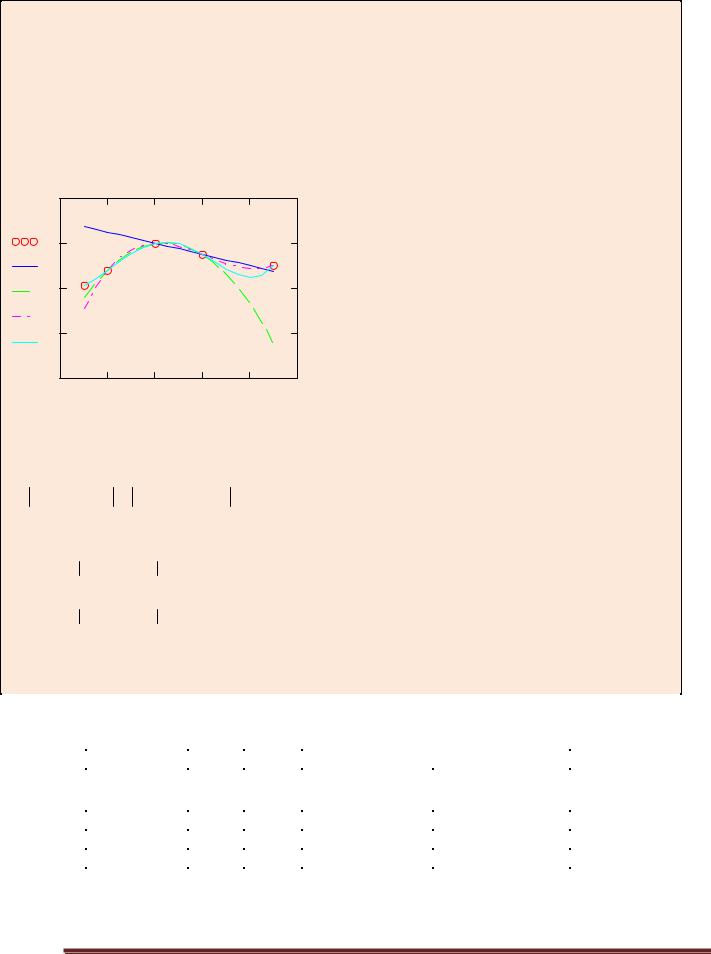
Графики табличной и интерполирующих функций по формуле Лагранжа: t 1 1.5 9
|
40 |
|
|
|
|
|
yi |
20 |
|
|
|
|
|
L1(t) |
|
|
|
|
|
|
L2(t) |
0 |
|
|
|
|
|
L3(t) |
|
|
|
|
|
|
f(t) 20 |
|
|
|
|
|
|
400 |
2 |
4 |
6 |
8 |
10 |
|
|
|
|
|
xi t |
|
|
Оценку погрешности многочлена Лагранжа практически производят по формуле:
f (x) Ln (x) Ln 1(x) Ln (x)
Таким образом, погрешности многочленов Лагранжа равны
для линейной интерполяции:
R1 L2(5) L1(5) 2.125
дляквадратичной интерполяции:
R2 L3(5) L2(5) 0.982
длякубической интерполяции:
|
R3 |
f (5) L3(5) |
1.029 |
|
|
|
|
|
|
Запишем в табл. 3-3 результаты интерполяции и оценки погрешности (здесь приведены результаты интерполяции только для первой формулы Ньютона):
|
Число |
|
|
|
Оценка погрешности |
|
|
Узлов |
|
|
|
Метод Ньютона |
Метод Лагранжа |
|
n+1 |
|
Pn (a) |
Ln(b) |
| Rn (a)| |
|Rn(b)| |
|
2 |
|
-0.5 |
17.5 |
7.5•10-3 |
2.125 |
|
3 |
|
-0.507 |
19.625 |
0.066 |
0.982 |
|
4 |
|
-0.574 |
18.643 |
0.084 |
1.029 |
Тема1.3. Интерполяция функций (Лабораторныйпрактикум) |
Страница 11 |

4. Интерполяционные многочлены в явном виде и значения построенных многочленов во всех выбранных узлах интерполяции.
Приведем пример выполнения задания для многочленов Ньютона, построенных ранее (при выполнении п.2 лабораторной работы) по первой формуле. Упростим выражения и вычислим значения во всех узлах интерполяции.
Многочлен Ньютона 1 степени
P1(x) 3.8x 2.02
|
|
|
|
|
P1(0.3) 0.88 |
P1(0.5) 0.12 |
P1(0.7) 0.64 |
P1(0.9) 1.4 |
P1(1.1) 2.16 |
Многочлен Ньютона 2 степени
P2(x) 0.75x2 3.2x 1.9075
P2(0.3) 0.88 P2(0.5) 0.12 P2(0.7) 0.7 P2(0.9) 1.58 P2(1.1) 2.52
Многочлен Ньютона 3 степени
P3(x) 22.0833x3 33.875x2 12.4792x 0.41125
|
|
|
|
|
P3(0.3) 0.88 |
P3(0.5) 0.12 |
P3(0.7) 0.7 |
P3(0.9) 0.52 |
P3(1.1) 1.72 |
Многочлен Ньютона 4 степени
P4(x) 56.25x4 157.0833x3 149.75x2 54.3292x 5.7269
|
|
|
|
|
|
|
|
P4(0.3) 0.88 |
P4(0.5) 0.12 |
P4(0.7) 0.7 |
P4(0.9) 0.52 |
P4(1.1) 0.44 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Занесем в таблицу 3-4 значения построенных многочленов в узлах интерполяции и сравним с заданными значениями исходной функции:
|
xi |
|
0.3 |
|
0.5 |
|
0.7 |
|
0.9 |
|
1.1 |
|
|
P1(xi) |
|
-0.88 |
|
-0.12 |
|
0.64 |
|
1.4 |
|
2.16 |
|
|
P2(xi) |
|
-0.88 |
|
-0.12 |
|
0.7 |
|
1.58 |
|
2.52 |
|
|
P3(xi) |
|
-0.88 |
|
-0.12 |
|
0.7 |
|
0.52 |
|
-1.72 |
|
|
P4(xi) |
|
-0.88 |
|
-0.12 |
|
0.7 |
|
0.52 |
|
0.44 |
|
|
Исходная функция |
|
-0.88 |
|
-0.12 |
|
0.7 |
|
0.52 |
|
0.44 |
|
|
y=f(xi) |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Тема1.3. Интерполяция функций (Лабораторныйпрактикум) |
Страница 12 |

3.6. Контрольные вопросы по теме
Интерполяция функций
1.Что называется задачей интерполяции и задачей аппроксимации?
2.Что называется узлами и шагом интерполяции?
3.Что такое интерполируемая функция и интерполирующая функция?
4.Существует ли связь между числом узлов интерполяции и степенью интерполяционного многочлена?
5.Что обеспечивает единственность решения полиномиального интерполирования?
6.Можно ли, используя одни и те же узлы интерполяции, построить несколько интерполяционных полиномов?
7.Сколько интерполяционных полиномов степени n существует, если функция задана (n + 1) узлом?
8.Изменится ли точность интерполяции при увеличении или уменьшении количества узлов?
9.Какой метод интерполяции позволяет обеспечить наименьшую погрешность при вычислении значения функции в точке x, находящейся в начале таблицы с равноотстоящими узлами?
10.Какой метод интерполяции позволяет обеспечить наименьшую погрешность при вычислении значения функции в точке x, находящейся в конце таблицы с равноотстоящими узлами?
11.Как изменится формула Лагранжа при добавлении в таблицу значений функции еще одного узла?
12.Какой степени является полином, полученный с использованием формулы Лагранжа при использовании n + 1 узлов таблицы?
13.Если интерполируемая функция f(x)задана в (n + 1) равноотстоящих узлах, то для ее интерполяции удобнее использовать формулу Ньютона или формулу Лагранжа?
14.Какой степени является полином, полученный с использованием формулы Ньютона при использовании n + 1 равноотстоящих узлов таблицы?
15.Можно ли при использовании формулы Лагранжа располагать узлы интерполяции в произвольном порядке?
16.Потребуется ли полный пересчет коэффициентов формулы Лагранжа при добавлении дополнительного узла интерполяции?
17.В чем заключается универсальность формулы Лагранжа?
18.От чего зависит точность интерполяции?
19.Можно ли при использовании интерполяционных формул Ньютона располагать узлы в произвольном порядке?
20.Что такое «конечные разности»?
21.Чему равен порядок конечной разности наивысшего порядка, полученный по n исходным точкам?
22.Что происходит с формулой Ньютона при добавлении очередного узла интерполяции?
23.Чем отличаются результаты интерполяции, если при построении интерполяционных полиномов по формулам Лагранжа и Ньютона были использованы одни и те же узлы?
24.Чему равна степень интерполяционного полинома Ньютона при трех заданных точках
интерполируемой функции?
25. Если интерполируемая функция задана аналитическим выражением, требуется ли для решения задачи интерполяции предварительно рассчитать значения функции в узлах?
Тема1.3. Интерполяция функций (Лабораторныйпрактикум) |
Страница 13 |
Тема 4. Лабораторная работа Численное интегрирование
4.1.Вопросы, подлежащие изучению
1.Постановка задачи численного интегрирования.
2.Методы прямоугольников, трапеций, Симпсона.
3.Оценка погрешности численного интегрирования. Правило Рунге.
4.Графическая иллюстрация методов прямоугольников, трапеций и Симпсона.
4.2.Задание
1.Выбрать индивидуальное задание из табл.4-1 для численного интегрирования:
f(x) – подынтегральную функцию;
a, b– пределы интегрирования;
метод интегрирования для выполнения п.2 – значение в столбце t;
метод интегрирования для выполнения п.3 – значение в столбце m;
начальный шаг интегрирования h0.
Значения в столбцах t и m означают: 1 –интегрирование методом средних прямоугольников, 2 – методом трапеций, 3 – методом Симпсона.
2. |
Вычислить «вручную» интеграл I b f(x)dx с шагом h0 и h0 /2 по выбранному методу |
|
a |
|
численного интегрирования (значение в столбце t табл.4-1, или по указанному |
|
преподавателем) без использования пакета MathCad (или используя пакет только как |
|
калькулятор) и оценить погрешность интегрирования по правилуРунге. |
3. |
Вычислить «вручную» интеграл I b f(x)dx с шагом h0 и h0 /2 по выбранному методу |
a
численного интегрирования (значение в столбце m из табл.4-1, или по указанному преподавателем) используя пакет MathCad для записи формул соответствующих методов (вычисления сумм ( ∑ ) значений функции и т.п.). Оценить погрешность по правилу Рунге.
4. Вычислить интеграл I b f(x)dx с помощью встроенных функций математического
a
пакета MathCad
4.3. Варианты задания
Таблица 4-1
№ |
f(x) |
a |
b |
t |
m |
h0 |
|
1 |
8 e-x sin(-2x) |
2 |
3 |
1 |
|
3 |
0.25 |
|
|
2 |
e-x sin(2x) |
0 |
2 |
2 |
|
1 |
0.5 |
|
|
3 |
x3/2 – 2 x sin(x) |
3 |
4 |
3 |
|
2 |
0.25 |
|
|
4 |
e-xcos(-2x) |
2 |
4 |
1 |
|
3 |
0.5 |
|
|
5 |
cos(2x) + 2 sin(x) |
1 |
3 |
2 |
|
1 |
0.5 |
|
|
6 |
8 sin(2x) – x |
0.2 |
1.2 |
3 |
|
2 |
0.25 |
|
|
7 |
5 cos(-2x) e-x |
-0.5 |
0.5 |
2 |
|
3 |
0.25 |
|
|
8 |
x sin(x + 1) – cos(x – 5) |
1 |
2 |
1 |
|
2 |
0.25 |
|
|
9 |
0,25 x3 + cos(x/4) |
1 |
3 |
1 |
|
3 |
0,5 |
|
|
10 |
sin(2x) – 2 sin(x) |
3 |
5 |
1 |
|
3 |
0.5 |
Страница 1 |
Тема1.4.Численноеинтегрирование (Лабораторный практикум) |
|
|
|||||||

11 |
sin(ex) – e-x +1 |
0 |
1 |
2 |
1 |
0.25 |
12 |
5 x sin(x + 1) + 2 cos(x) |
1 |
2 |
1 |
2 |
0.25 |
13 |
5 e-x + 4 x + x3/3 |
-1 |
1 |
1 |
2 |
0.5 |
14 |
-2 sin(4x) ln(-x) + 5 |
-2.5 |
-1.5 |
1 |
3 |
0.25 |
15 |
sin(x – 1) – x cos(x + 3) |
-4 |
-2 |
3 |
1 |
0.5 |
16 |
4 sin (x) – x1/2 |
1 |
2 |
2 |
3 |
0.25 |
17 |
5 sin3(x) + cos3(x) |
1 |
2 |
2 |
1 |
0.25 |
18 |
cos(2x + 1) ln (2 / x) + 3 |
1 |
3 |
3 |
2 |
0.5 |
19 |
3 cos(x2) / ln(x + 5) |
-1 |
1 |
1 |
3 |
0.5 |
20 |
sin(x2) + 1 / (2 – x) |
-1.5 |
0.5 |
2 |
1 |
0.5 |
21 |
x sin(x) + cos(x) + 5 |
0 |
2 |
1 |
2 |
0.5 |
22 |
– cos(x) – cos(2x) – x + 5 |
1 |
3 |
3 |
1 |
0.5 |
23 |
1 + sin(4x) / ln(x) |
1.5 |
2.5 |
1 |
3 |
0.25 |
24 |
(1 + x2)1/2 + e-x |
-1 |
2 |
2 |
1 |
0.75 |
25 |
sin(x + 1) e2 / x |
1 |
2 |
3 |
2 |
0.25 |
26 |
2 (1 + x) e-x – 2 cos(x) |
1 |
4 |
2 |
3 |
0.75 |
27 |
– 8 sin(– x3) e-x |
0.4 |
1.4 |
1 |
3 |
0.25 |
28 |
– 10 sin(x3) cos(– x) |
-1.4 |
-0.4 |
2 |
1 |
0.25 |
29 |
x2cos(x + 3) – 4 |
3 |
4 |
3 |
1 |
0.25 |
30 |
– cos(x – 5) e2x / 3 |
1 |
3 |
1 |
3 |
0.5 |
31 |
x - cos(x/3) |
2 |
3 |
1 |
2 |
0,25 |
32 |
x + ln(4x) – 1 |
0 |
2 |
2 |
3 |
0,5 |
33 |
ex- 4e-x – 1 |
3 |
4 |
3 |
1 |
0,25 |
34 |
x ex– 2 |
2 |
4 |
1 |
2 |
0,5 |
35 |
4(x2+1) ln(x) – 1 |
1 |
3 |
2 |
3 |
0,5 |
36 |
2 – x - sin(x/4) |
0,2 |
1,2 |
3 |
2 |
0,25 |
37 |
x2 + ln(x) – 2 |
-0,5 |
0,5 |
2 |
3 |
0,25 |
38 |
сos(x) - (x+2)½ + 1 |
1 |
2 |
1 |
2 |
0,25 |
39 |
4(1+x1/2) ln(x) – 1 |
1,2 |
3,2 |
3 |
1 |
0,5 |
40 |
5ln(x) - x1/2 |
3,5 |
5 |
1 |
3 |
0,5 |
41 |
ex+ x3 –2 |
0 |
1 |
2 |
3 |
0,25 |
42 |
3sin(x1/2) + x – 3 |
1 |
2 |
1 |
2 |
0,25 |
43 |
0,1 x2 – x ln(x) |
-1 |
1 |
1 |
3 |
0,5 |
44 |
cos(1 + 0,2x2) – x |
-2,5 |
-1,5 |
1 |
1 |
0,25 |
45 |
3 x – 4 ln(x) – 5 |
-4 |
-2 |
3 |
2 |
0,5 |
4.4.Содержание отчета
1.Индивидуальное задание.
2. |
Результаты «ручного расчета» |
интеграла с шагом h0 |
и h0 /2 |
(Ih0 |
и |
Ih0/2 ) без |
|
|
использования пакета MathCad (или используя пакет только как калькулятор) и |
значения |
|||||
3. |
погрешностей по правилуРунге. |
|
|
|
|
|
|
Результаты «ручного расчета» |
интеграла с шагом h0 |
и h0 /2 |
(Ih0 |
и |
Ih0/2 ) при |
||
|
использовании |
пакета MathCad для записи формул |
соответствующих |
методов |
|||
|
(вычисления сумм ( ∑ ) значений функции и т.п.) и значения погрешностей по правилу |
||||||
|
Рунге. |
|
|
|
|
|
|
4.Результаты решения, полученные с помощью встроенных функций математического пакета.
Тема1.4.Численноеинтегрирование (Лабораторный практикум) |
Страница 2 |

4.5. Пример выполнения задания
1. Задание для численного интегрирования:
ln(x) – подынтегральная функция;
a=1, b=3–пределы интегрирования;
методы интегрирования для выполнения п.2 – средних прямоугольников, трапеций, Симпсона;
методы интегрирования для выполнения п.3 – средних прямоугольников, трапеций, Симпсона;
начальный шаг интегрирования h0=1.
2.«Ручной расчет» интеграла с шагом h0 =1 и h0 /2 (Ih0 и Ih0/2 ) и оценка его погрешности по правилу Рунге, при использовании MathCad только как калькулятора
В качестве примера рассмотрим вычисление интеграла 3 |
ln xdx с шагом h0=1 и |
h0 |
0.5 |
1 |
|
2 |
|
методами средних прямоугольников, трапеций и Симпсона.
Правило Рунге применяют для вычисления погрешности путём двойного просчёта интеграла с шагами h/2 и h, при этом погрешность вычисляется по формуле R Ih/22P 1Ih .
Полагают, что интеграл вычислен с точностью |
Е, если |
|
R |
|
E , тогда |
I Ih/2 |
R, где I – |
|||||
|
|
|||||||||||
уточненное значение интеграла, p – порядок метода. |
|
|
|
|
|
|
|
|||||
Вычислим интеграл 3 |
ln xdx с шагом h0=1 и h0 |
0.5 по формуле |
|
|
|
|||||||
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
средних |
прямоугольников |
b |
n 1 |
|
|
|
|
|
погрешность |
|||
f(x)dx |
h f(a h i h)и оценим |
|||||||||||
|
|
|
|
a |
i 0 |
2 |
|
|
|
|||
интегрирования методом двойного просчёта: |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
f (x) ln(x) h 1 |
|
|
|
|
|
|
|
|
|
||
|
x 1 1.25 3 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
f(x) |
|
|
|
|
|
|
|
|
|
|
1 0
1.250.223144
1.50.405465
1.750.559616
2 0.693147
2.250.81093
2.50.916291
2.751.011601
|
3 |
|
|
1.098612 |
|
|
|
|
|
|
|
|
|
||
I1 h (f (1.5) f (2.5)) |
1.321756 |
|
|
||||
I2 |
h (f(1.25) f(1.75) |
f(2.25) |
f(2.75)) |
1.302645 |
|||
|
2 |
|
|
|
|
|
|
|
I2 I1 |
|
3 |
|
|
||
R |
3 |
|
6.3702 |
10 |
|
|
|
Isr I2 R |
1.296275 |
|
|
|
|||
|
|
|
|
Тема1.4.Численноеинтегрирование (Лабораторный практикум) |
Страница 3 |
||

трапеций |
|
b |
|
|
(y0 |
n 1 |
yi f(xi)и оценим погрешность |
||||
|
f(x)dx h |
yn 2 yi ),где |
|||||||||
|
|
|
|
|
a |
2 |
|
i 1 |
|
|
|
интегрирования методом двойного просчета: |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
f (x) ln(x) |
h 1 |
|
|
|
|
|
|
||
|
|
x 1 1.5 3 |
|
|
|
|
|
|
|
||
|
|
x |
f(x) |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
|
|
|
|
|
||
1.50.405465
2 0.693147
2.50.916291
3 1.098612
I1 |
h |
(f(1) |
f(3) |
2f |
(2)) 1.242453 |
|
|||
|
2 |
|
|
|
|
|
|
|
|
I2 |
h |
[f(1) |
f(3) |
2 (f(1.5) |
f(2) f(2.5))] |
1.282105 |
|||
4 |
|||||||||
|
|
|
|
|
|
|
|
||
R |
I2 I1 |
|
0.01322 |
|
|
|
|||
|
|
3 |
|
|
|
|
|
|
|
Itrap I2 R 1.295322
Симпсона
b f(x)dx h[y0 y2m 4(y1 y3 ... y2m 1) 2(y2 y4 ... y2m 2)] |
|||
a |
3 |
|
|
где |
yi f(xi), |
n 2 m четное |
число |
и оценим погрешность интегрирования методом двойного просчета:
f (x) ln(x) |
h |
1 |
|
x |
1 1.5 3 |
|
|
x |
f(x) |
|
|
1 0
1.50.405465
2 0.693147
2.50.916291
|
|
3 |
|
|
1.098612 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
I1 |
|
h |
(f(1) |
f(3) |
4 f(2)) |
1.2904 |
|
||
|
3 |
|
||||||||
|
|
|
|
|
|
|
|
|
||
|
I2 |
|
h |
[f(1) |
f(3) |
4 (f(1.5) |
f(2.5)) 2 f(2)] |
1.295322 |
||
|
6 |
|||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
I2 I1 |
|
|
4 |
|
|
||
|
R |
|
|
15 |
|
3.28089 10 |
|
|
||
|
Isimp I2 |
R 1.29565 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Тема1.4.Численноеинтегрирование (Лабораторный практикум) |
Страница 4 |

3. «Ручной расчет» интеграла с использованием MathCad с шагом h0 и h0 /2 и оценка его погрешности по правилу Рунге
поформулесреднихпрямоугольников:
f(x) lnx( ) |
|
a 1 |
b 3 |
|
|
|
|
|
|
||||||
h 1 |
n |
(b a) |
i 0 n 1 |
xi |
a h |
i h |
yi f xi |
Ip1 h yi |
Ip1 1.3218 |
||||||
|
|
h |
|
||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
i |
|
|||
h h |
|
(b a) |
|
|
a h |
|
|
|
|||||||
n |
i 0 n 1 |
xi |
i h |
yi f xi |
Ip2 h yi |
Ip2 1.3026 |
|||||||||
|
|
h |
|
||||||||||||
2 |
Ip1 Ip2 |
|
|
|
2 |
|
|
i |
|
||||||
|
|
|
|
|
|
3 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
R |
|
|
|
|
|
R 6.3702 10 |
|
|
|
|
|
|
|||
|
|
3 |
|
|
|
|
|
|
|
|
|||||
поформулетрапеций:
f (x) ln(x) h 1 a 1 b 3
n
I1
b a |
|
2 |
i 0 n |
xi a i h |
yi f xi |
||
|
|
h |
|||||
|
h |
n 1 |
|
|
|
|
|
|
|
yi |
yi 1 |
1.242453 |
|
||
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
i 0 |
|
|
|
|
|
h |
h |
0.5 |
n |
b a |
4 |
i |
0 n |
xi |
a |
i h |
yi f xi |
2 |
h |
I2
R
n 1
i 0h
I2 I1
3
yi yi 1 1.282105
0.01322
поформулеСимпсона:
f (x) ln(x) h 1 a 1 b 3
|
n |
b a |
2 |
|
i 0 n |
xi a i h |
yi f xi |
|
|
|||||||||||
|
|
|
h |
|
|
|
|
|||||||||||||
|
I1 |
h |
y |
|
y |
|
4y |
1.2904 |
|
|
|
|
|
|||||||
3 |
|
0 |
n |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
h |
|
h |
0.5 |
n |
b a |
|
4 i |
0 n |
xi a i h |
yi f xi |
|
||||||||
|
2 |
|
h |
|
||||||||||||||||
|
m |
1 3 n 1 |
|
k 2 4 n |
2 |
|
|
|
|
|
||||||||||
|
I2 |
h |
y0 yn |
4 |
ym |
2 yk |
1.295322 |
|
|
|||||||||||
3 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
k |
|
|
|
|
|
|
|
|
|
I2 I1 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|||||
|
R |
|
|
|
|
|
|
|
3.28089 10 |
|
|
|
|
|
|
|||||
|
|
|
15 |
|
|
|
|
|
|
|
|
|
||||||||
Тема1.4.Численноеинтегрирование (Лабораторный практикум) |
Страница 5 |
|||||||||||||||||||

4. Результаты решения задачи с помощью математического пакета Mathcad
Для вычисления определенного интеграла с использованием пакета используется шаблон, который вызывается кнопкой с изображением определенного интеграла с дополнительной панели Операции математического анализа панели Математика:
3
f(x) ln(x) f(x) dx 1.2958
1
4.6.Контрольные вопросы по теме Численное интегрирование
1.Что такое шаг интегрирования?
2.По какой формуле вычисляется шаг изменения х на отрезке [a;b]?
3.Каким образом связана задача численного интегрирования и интерполяция?
4.Какое влияние оказывает уменьшение числа разбиений на отрезке [a;b] на погрешность интегрирования?
5.Каким образом вычисляется определенный интеграл в случае, если подынтегральная функция задана таблицей с переменным шагом?
6.Какой из изученных вами методов численного интегрирования обладает высшей степенью точности?
7.Зависит ли точность численного интегрирования от величины шага интегрирования?
8.Для чего предназначен метод двойного просчета?
9.Какие методы относятся к методам численного интегрирования?
10.Что представляет собой формула для вычисления элементарного интеграла по формуле трапеций?
11.Что представляет собой формула для вычисления элементарного интеграла по формуле Симпсона?
12.Интерполяционным многочленом какой степени заменяется подынтегральная функция в методе прямоугольников?
13.Интерполяционным многочленом какой степени заменяется подынтегральная функция в методе трапеций?
14.Как называется метод численного интегрирования, в котором подынтегральная функция заменяется полиномом нулевой степени?
15.В каком методе для вычисления интеграла необходимо выбирать количество интервалов разбиения кратное двум?
16.Какой метод численного интегрирования даст наиболее точный результат, если подынтегральная функция имеет вид y = 5x3?
17.В каком методе численного интегрирования подынтегральная функция заменяется квадратичным полиномом?
18.Какой метод численного интегрирования даст точный результат, если подынтегральная функция имеет вид f(x) = x2?
19.Какой метод интегрирования наилучшим образом подходит для вычисления интеграла линейной функции?
20.Обеспечивают ли методы трапеций и метод средних прямоугольников точность одного порядка?
21.Какой из известных вам методов интегрирования обладает наименьшей точностью?
22.Какому числу кратно количество интервалов разбиения в методе Симпсона?
23.Позволяет ли метод прямоугольников получить точное значение интеграла, если подынтегральная функция – полином 0-й степени?
Тема1.4.Численноеинтегрирование (Лабораторный практикум) |
Страница 6 |

Тема 5. Лабораторная работа Методы решения
обыкновенных дифференциальных уравнений»
5.1.Вопросы, подлежащие изучению
1.Постановка задачи численного решения обыкновенных дифференциальных уравнений. Задача Коши.
1.Методы Рунге-Кутты различных порядков, общие свойства.
2.Погрешности методов.
3.Выбор шага интегрирования.
4.Графическая иллюстрация методов Рунге-Кутты.
5.2.Задание
1.Выбрать индивидуальное задание в табл. 5-1 для решения обыкновенных дифференциальных уравнений:
дифференциальное уравнение y' f(x,y);
интервал [a;b] , где ищется решение дифференциального уравнения;
начальные условия x0, y0;
шаг интегрирования h.
2.Найти аналитическое решение y(x) заданного дифференциального уравнения, полагая его точным.
3.Вычислить значения полученного решенияy(x) на отрезке [a;b] с шагом h.
4.Найти численное решение дифференциального уравнения методом Эйлера –
функцию ye(x) в первых 4-х точках отрезка [a;b] с шагом h «расчетом вручную» (можно использовать математический пакет только как калькулятор). Оценить погрешности полученного решения по методу двойного просчета (правилу Рунге).
5.Найти численное решение дифференциального уравнения методом Эйлера –
функцию y1(x) во всех точках отрезка [a;b] с шагом h, используя математический пакет.
6.Найти численное решение дифференциального уравнения методом Рунге-Кутты 2
порядка – функцию y2(x) в точках отрезка [a;b] с шагом h, используя математический пакет.
7.Найти численное решение дифференциального уравнения методом Рунге-Кутты 4
порядка – функцию y4(x) в точках отрезка [a;b] с шагом h, используя математический пакет.
8.Вычислить значения погрешностей численного решения дифференциального уравнения для каждого метода.
9.Графически проиллюстрировать полученныерешения.
Тема1.5.Методы решенияОДУ (Лабораторный практикум) |
Страница 1 |
