Выбор начальных приближений

Для первого корня (используется метод Ньютона) начальное приближение x₀ должно удовлетворять условию * > 0, т.е. за начальное приближение следует принять тот конец отрезка, где знак функции и знак второй производной совпадают. Поскольку > 0 и > 0, то выберем начальное приближение к корню: 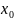= 3.65.

Для второго корня (используется метод итераций) выберем произвольное значение из отрезка [6.5; 7], например, x₀ = 6.5.

«Ручной расчет» трех итераций

Для уточнения первого корня методом Ньютона воспользуемся формулой .

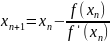Результаты вычислений сведены в Таблица 1.

Таблица 1

k	xk	f(xk)
0	3.65	0.52686
1	3.59843	6.55707*10-4
2	3.5983639169	1.67973*10-9
3	3.5983639167	0

Для уточнения второго корня методом итераций воспользуемся формулой .

Результаты вычислений сведены в Таблица 2.

Таблица 2

k	xk	f(xk)
0	6.5	3.77525
1	6.93893	-0.18361
2	6.91758	-5.86785*10-3
3	6.9169	-1.47212*10-4

Оценка погрешностей по формулам оценки погрешностей соответствующих методов

Для уточнения первого корня используется метод Ньютона. Для оценки погрешности метода Ньютона справедливо соотношени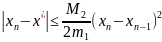е: , где 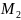- наибольшее значение 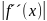, 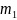- наименьшее значение на отрезке [a; b].

Оценим погрешность после трех итераций:

m₁ = 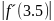= 10.06301, M₂ = 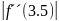= 1.69124,

Тогда .

Для уточнения второго корня используется метод итераций. Для оценки погрешности метода итерации справедливо соотношение 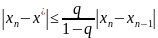, где q = max|φˊ(x)| на выбранном отрезке.

В нашем случае q = |φˊ(6.55) = 0.084. Оценим погрешность результата после трех итераций: = .

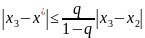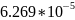Решение уравнения средствами Mathcad

Для решения нелинейных уравнений вида f(x) = 0 в Mathcad используется функция root(f(x), x, a, b), где f(x) - выражение, стоящее в левой части решаемого уравнения, x - аргумент функции, a и b - границы отрезка с корнем.

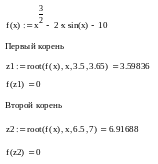
Вычисление значения определенного интеграла «Ручной расчет» интеграла с шагом и

Формула для метода средних прямоугольников: .

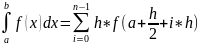1. С использованием Mathcad только как калькулятора:

2. С использованием Mathcad для записи формул соответствующих методов:

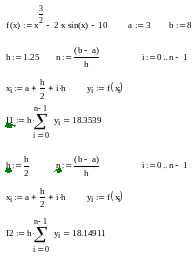
Формула для метода трапеций: .

1. С использованием Mathcad только как калькулятора:

2. С использованием Mathcad для записи формул соответствующих методов:

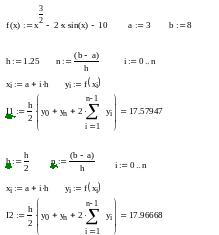
Формула для метода Симпсона:

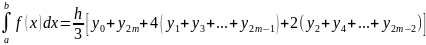
1. С использованием Mathcad только как калькулятора:

2. С использованием Mathcad для записи формул соответствующих методов:

Оценка погрешности интегрирования по правилу Рунге

Правило Рунге применяют для вычисления погрешности путем двойного просчета интеграла с шагами h и h/2, при этом погрешность вычисляется по формуле 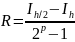. Полагают, что интеграл вычислен с точностью 𝜀, если |R| ≤ 𝜀; тогда I = I_h/2 + R, где I - уточненное значение интеграла, p - порядок метода.

Оценим погрешность интегрирования по методу средних прямоугольников. Порядок этого метода равен 2.

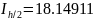
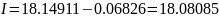
Оценим погрешность интегрирования по методу трапеций. Порядок этого метода равен 2.

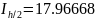
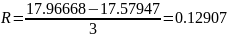
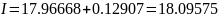
Оценим погрешность интегрирования по методу Симпсона. Порядок этого метода равен 4.

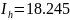
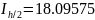
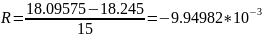
Расчет средствами Mathcad и 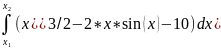, где x₁ и x₂ - корни уравнения

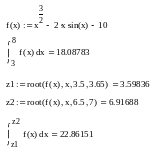
Определение точки экстремума функции 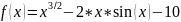двумя методами одномерной оптимизации (дихотомии и золотого сечения)

Для нахождения экстремума применим методы дихотомии и золотого сечения, причем для нахождения максимума следует ввести новую функцию .

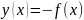Проверка условия унимодальности функции и выбор начального отрезка оптимизации

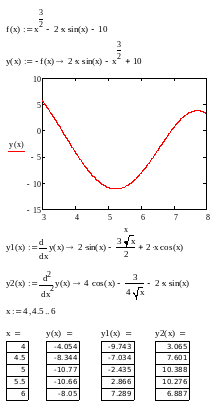
Из приведенных расчетов видно, что на отрезке [4;6] функция y(x) - унимодальная, ее первая производная монотонно возрастает, а вторая производная больше нуля. Следовательно, этот отрезок может быть выбран в качестве начального отрезка неопределенности.

Проведение «ручного расчета» по сокращению отрезка оптимизации и проверка условия окончания поиска максимума функции

Метод дихотомии

Условие окончания поиска максимума функции: 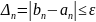, где - длина n-ого отрезка неопределенности.

Результаты вычислений сведены в Таблица 3.

Таблица 3

N	a	b	x1	x2	y(x1)	y(x2)	𝛥n
1	4	6	4.998	5.002	-10.76469	-10.77443	2
2	4.998	6	5.497	5.501	-10.66814	-10.65672	1.002
3	4.998	5.501	5.2475	5.2515	-11.0486	-11.04773	0.503
4	4.998	5.2515					0.2535

После 3-х итераций за максимум можно принять середину оставшегося отрезка, т.е. координатами точки максимума можно считать x_max ≈ 5.12475, f(x_max) ≈ 10.99172

При заданной точности 𝜀 = 0.01 после 3-х итераций условие окончания поиска максимума функции не выполнено.