Федеральное Агентство Связи Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технический университет связи и информатики»

Центр заочного обучения по программам бакалавриата

Кафедра информатики

Отчет по курсовой работе «Практическое решение инженерных и научных задач на пк с использованием математических пакетов» Вариант №24

Выполнил: Иванов Иван, студент группы БСТ17хх

Проверил:

Общее задание

1. Выбрать вариант задания в соответствии с номером в журнале группы.

2. Найти два корня уравнения (x₁ и x₂) заданной функции на заданном интервале [a; b] указанными методами. Для этого необходимо:

• отделить корни уравнения;

• проверить (аналитически) условия сходимости применяемых методов решения уравнений (в случае необходимости привести уравнение к виду, обеспечивающему сходимость процесса приближения к корню);

• выбрать начальные приближения;

• записать рекуррентную формулу для уточнения корня и произвести по ней «ручной расчет» 3-х итераций;

• оценить погрешности по формулам оценки погрешности соответствующего метода;

• вычислить значения корней «расчетом средствами Mathcad».

3. Вычислить значение определенного интеграла, для чего:

• произвести «ручной расчет» 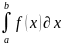с шагом h₀ и h₀/2 (где a, b - заданный интервал) методами средних прямоугольников, трапеций и Симпсона в двух вариантах для каждого метода: 1) без использования пакета Mathcad (или используя пакет только как калькулятор), и 2) используя пакет Mathcad для записи формул соответствующих методов (вычисления сумм значений функции и т.п.);

• оценить погрешность интегрирования по правилу Рунге;

• вычислить значения и 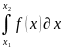(где x₁ и x₂ - корни уравнения f(x) = 0) с использованием «расчета средствами Mathcad».

4. Определить точку экстремума функции f(x) двумя методами одномерной оптимизации (дихотомии и золотого сечения), для чего:

• проверить условие унимодальности функции и выбрать начальный отрезок оптимизации;

• провести «ручной расчет» по сокращению отрезка оптимизации и проверить условие окончания поиска минимума (максимума) функции;

• определить точку экстремума функции f(x) «расчетом средствами Mathcad».

Индивидуальное задание

• исследуемая функция - ;

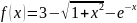• заданный интервал - [-1; 3];

• используемый метод для вычисления первого корня - метод итерации;

• используемый метод для вычисления второго корня – метод половинного деления;

• начальный шаг интегрирования - h₀ = 1.

Нахождение двух корней уравнения f(x) = 0 на заданном интервале

Отделение корней уравнения

Построим график заданной функции:

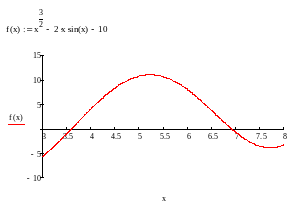
Отделим корни уравнения аналитически для двух предполагаемых интервалов:

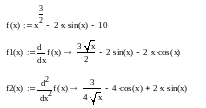
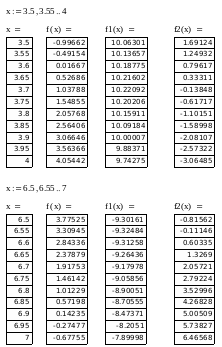
На отрезках [3.5; 4] и [6.5; 7] функция f(x) меняет знак, т.е. существует, по крайней мере, по одному корню. Поскольку знак первой производной на выбранных отрезках остается постоянным, то можно сказать, что функция на этих отрезках монотонна. Следовательно, выбранные отрезки содержат по одному корню.

Проверка условий сходимости применяемых методов решения уравнений

Для уточнения первого корня на отрезке [3.5; 4] будет использоваться метод Ньютона. Необходимые и достаточные условия сходимости метода Ньютона: 1) 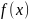непрерывна на [a; b] и 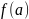* 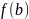< 0, и 2) 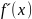и 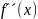отличны от нуля и сохраняют знаки для xÎ [a; b].

На отрезке [3.5; 4] вторая производная меняет знак. Следовательно, надо подобрать меньший отрезок, расположенный внутри отрезка [3.5; 4], так, чтобы знак второй производной (и первой тоже) был постоянен, а сама функция f(x) меняла знак. В нашем случае можно выбрать отрезок [3.5; 3.65]. Условия сходимости метода Ньютона на этом отрезке выполняются.

Для уточнения второго корня на отрезке [6.5; 7] будет использоваться метод итераций. Для этого необходимо привести уравнение f(x) = 0 к виду x = φ(x). Приведем уравнение 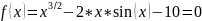к виду 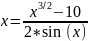. Для сходимости процесса итерации необходимо, чтобы |φˊ(x)| < 1, при xÎ[a; b]. Если |φˊ(x)| ≥ 1, то сходимость не обеспечена.

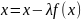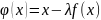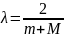Данная итерирующая функция не обеспечивает сходимость метода итераций. Поэтому приведем уравнение к виду , где итерирующая функция . Итерационный параметр 𝜆 выберем из условия , где m -минимальное, а M - максимальное по модулю значение f’(x) на отрезке [6.5; 7].

Таким образом, итерирующая функция, обеспечивающая сходимость метода, имеет вид .
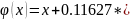