
Sb95798
.pdf
где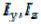 – осевые моменты инерции;
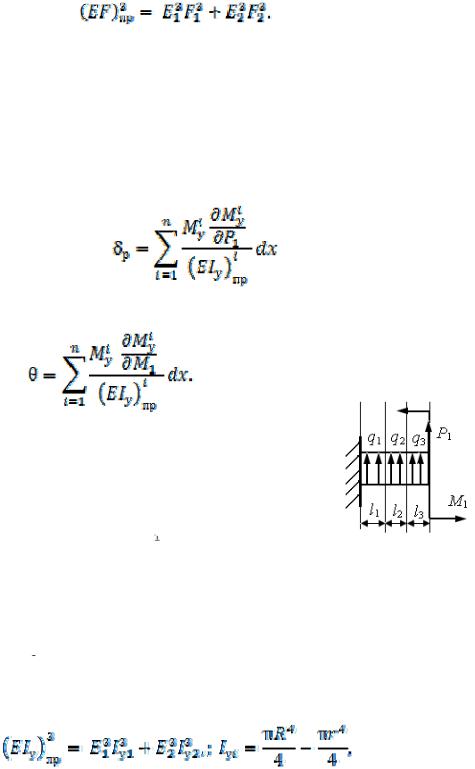
– осевые моменты инерции; 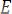 – модуль нормальной упругости.
– модуль нормальной упругости.
По закону Гука удлинение элемента стержня длиной 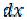 равно
равно
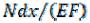 . Потенциальная энергия при растяжении-сжатии элементарного участка
. Потенциальная энергия при растяжении-сжатии элементарного участка
Слагаемые 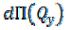 и
и 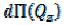 представляют потенциальную энергию
представляют потенциальную энергию
сдвига. При сдвиге для элемента стержня, учитывая закон Гука и формулу Журавского для касательных напряжений, можно записать:
где 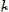


 и
и 

 – безразмерные величины, зависящие от геометрической формы
– безразмерные величины, зависящие от геометрической формы
сечения.
Как правило, эти слагаемые значительно меньше остальных, и ими можно пренебречь. Таким образом, потенциальная энергия деформации равна половине произведения сил или пары сил на перемещение по ее направлению в том сечении, где внутренняя сила приложена.
Сосредоточенную силу и сосредоточенный момент, вызывающие соответствующие перемещения, называют обобщенными силой и моментом, а перемещение, вызванное этой силой, – обобщенным перемещением.
Потенциальную энергию всего стержня найдем, проинтегрировав выражение для :
Теперь рассмотрим стержень длиной  , жестко защемленный одним концом. Известны геометрические характеристики стержня
, жестко защемленный одним концом. Известны геометрические характеристики стержня 
 ,
, 

 ,
, 
 , модуль
, модуль
нормальной упругости материала 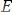 , модуль упругости при сдвиге
, модуль упругости при сдвиге 
 .
.
21
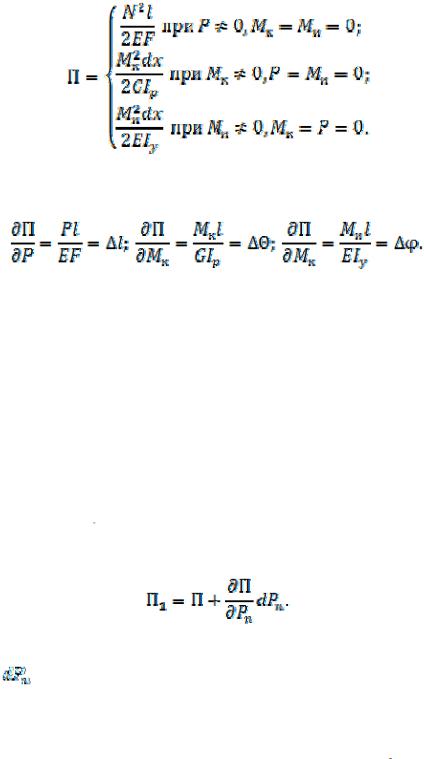
К свободному торцу стержня последовательно приложим растягивающую силу 
 , скручивающий момент
, скручивающий момент 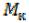 и изгибающий момент
и изгибающий момент 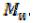 Накоп-
Накоп-
ленная в стержне потенциальная энергия упругой деформации численно равна работе каждой из этих внешних сил:
Рассмотрим производные от энергии упругой деформации по соответствующей обобщающей силе:
Производная от энергии упругой деформации по обобщенной силе равна перемещению, соответствующему этой силе по линии действия силы.
Эта закономерность в общем виде была установлена Кастильяно и сформулирована им в качестве теоремы.
Рассмотрим общий случай нагружения упругого тела. Пусть оно закреплено так, что при нагружении невозможно его смещение как жесткого целого. Тело испытывает деформацию под действием обобщенных сил  . Энергию упругой деформации выразим функцией этой группы
. Энергию упругой деформации выразим функцией этой группы
сил:  . Если одной из внешних сил, например
. Если одной из внешних сил, например , придать небольшое приращение
, придать небольшое приращение , то энергия упругой деформации возрастет:
, то энергия упругой деформации возрастет:
Возьмем другой случай. Допустим, сначала была приложена бесконечно малая сила , вызывающая бесконечно малое перемещение. Работой силы
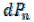 можно пренебречь как бесконечно малой величиной второго порядка по сравнению с работой приложенных затем сил
можно пренебречь как бесконечно малой величиной второго порядка по сравнению с работой приложенных затем сил 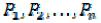 . Потенциальная энергия упругой деформации, вызванной этими силами, по-прежнему равна
. Потенциальная энергия упругой деформации, вызванной этими силами, по-прежнему равна
22
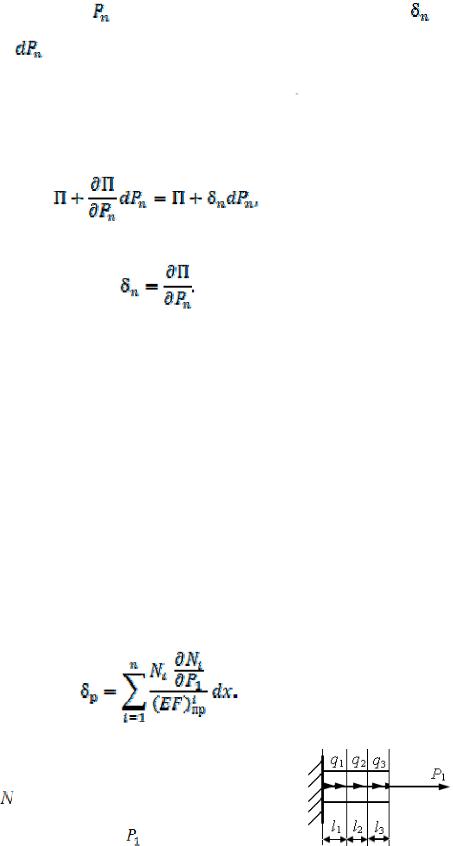
П. В точке приложения силы |
произойдет конечное перемещение , при |
котором малая сила , приложенная вначале, совершит работу 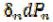 . Тогда накопленная потенциальная энергия
. Тогда накопленная потенциальная энергия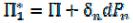 .
.
Потенциальная энергия деформации не зависит от порядка, в котором прикладываются силы, поэтому и, следовательно,
и, следовательно,
откуда
Сформулируем теорему Кастильяно:
Частная производная от потенциальной энергии упругой деформации по обобщенной силе равна обобщенному перемещению точки приложения силы по направлению силы.
Под перемещением в заданном направлении понимают проекцию полного перемещения на заданное направление. Перемещение точки приложения силы по направлению силы – это проекция на направление силы полного перемещения этой точки.
4.3.1. Расчет перемещений в точке узла конструкции при ускорении 5g, действующем вдоль оси конструкции
Рассмотрим стержень (рис. 4.5), который подвергается деформации рас- тяжения-сжатия. Перемещение определяется по формуле
Для определения перемещения крайней правой |
|
точки стержня необходимо записать выражения для |
|
нормальной силы на каждом грузовом участке, |
|
продифференцировать их по силе и найти значе- |
|
ния перемещений на каждом участке. |
Рис. 4.5 |
|
23
Значение 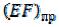 рассчитывается для каждого грузового участка исходя
рассчитывается для каждого грузового участка исходя
из данных о реальной конструкции. Например, рассмотрим третий грузовой участок. На этом участке схема состоит из двух элементов (см. рис. 4.1, а), расположенных параллельно. Следовательно, приведенное значение
Аналогично находятся значения и для остальных участков.
4.3.2. Расчет перемещений в точке узла конструкции при ускорении 5g, действующем по нормали к оси конструкции
Рассмотрим стержень (рис. 4.6), который подвергается деформации плоскопоперечного изгиба. При этом виде деформации возникает линейное перемещение по обобщенной силе
и угловое перемещение (угол поворота)
Для определения перемещения крайней правой точки стержня необходимо записать выражения для изгибающего момента 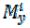 на каждом грузовом участке,
на каждом грузовом участке,
продифференцировать их по силе 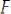
 для линейного пе-
для линейного пе-
Рис. 4.6
ремещения и по 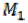 для угла поворота, а затем найти значения перемещений на каждом участке.
для угла поворота, а затем найти значения перемещений на каждом участке.
Значение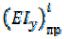 рассчитывается для каждого грузового участка исходя
рассчитывается для каждого грузового участка исходя
из данных о реальной конструкции. Для третьего грузового участка, состоящего из двух элементов (см. рис. 4.2, а), расположенных параллельно:
24

причем осевой момент инерции 


 рассчитывается отдельно для каждого
рассчитывается отдельно для каждого
элемента внутри этого участка.
Аналогично находятся значения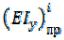 для остальных участков.
для остальных участков.
4.4. Определение низшей частоты собственных колебаний корпуса прибора
При эксплуатации приборы подвергаются динамическим воздействиям: ударам, за малый промежуток времени изменяющим скорости точек тела на конечное значение, и вибрациям, механическим колебаниям. Под колебаниями понимают движения или процессы, обладающие той или иной повторяемостью во времени.
Вибропрочность электронных приборов и устройств приобрела особое значение, как только эти приборы стали частью автоматизированных систем, применяемых в промышленности и на транспорте. Вредные, не являющиеся необходимым условием выполнения конструкцией своих функций, вибрации возникают из-за несовершенства конструкции, дефектов в ее элементах или особых условий действия и эксплуатации, например из-за несбалансированности деталей. Вибрации приводят к разрушению деталей и ослаблению зажимов и винтовых соединений. Если упругую систему вывести из равновесия, то силы упругости системы в новом положении уже не будут уравновешиваться и возникнут колебания.
При построении расчетной схемы наиболее легкие элементы конструкции можно считать безмассовыми, безынерционными деформируемыми связями.
Конструкция может быть описана системой с одной (рис. 4.7, а), двумя (рис. 4.7, б) или большим числом степеней свободы. Под числом степеней свободы понимают число независимых параметров, однозначно определяющих положение системы в данный момент времени. Любая конструкция содержит бесконечное число материальных точек и, следовательно, имеет бесконечное число степеней свободы. Стержень с распределенной массой представляет собой систему с бесконечным числом степеней свободы (рис. 4.7, в).
а |
б |
в |
|
||
|
Рис. 4.7 |
|
25
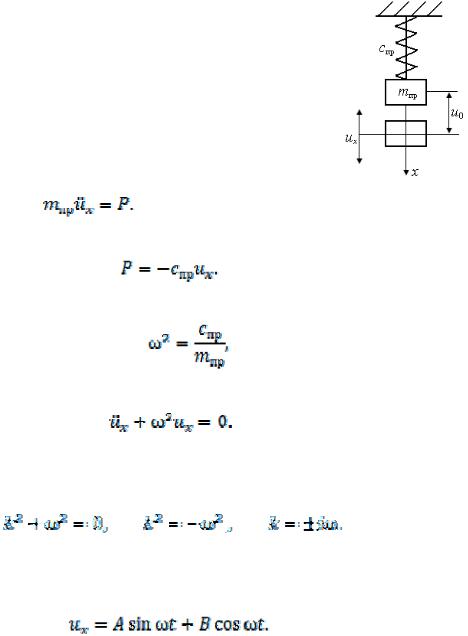
Собственные частоты колебаний являются обобщенными приведенными параметрами динамической расчетной схемы. Определение собственных частот колебаний – важная задача. Изделия при эксплуатации испытывают воздействие различных вынуждающих сил, переменных во времени, не зависящих от состояния системы и поддерживающих ее колебания. При совпадении или относительной близости собственных частот колебаний и частот вынуждающих сил появляются резонансные эффекты.
Рассмотрим линейные динамические расчетные схемы с одной степенью свободы.
Допустим, система, представленная на рис. 4.8, выведена из состояния статического равновесия. Инерционный элемент с приведенной массой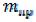 перемещен на
перемещен на
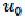 .
.
Внешние возбуждающие силы отсутствуют. Соста- |
|
вим уравнение движения, пользуясь вторым законом ди- |
|
намики: |
Рис. 4.8 |
|
Равнодействующая внешних сил равна восстанавливающей силе:
Введя обозначение
получим
Составим характеристическое уравнение по методу Эйлера 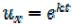 . Получим
. Получим
Для дальнейшего анализа показательные функции 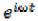 и
и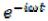 удобно представить тригонометрическими:
удобно представить тригонометрическими:
26

Постоянные интегрирования определяют из начальных условий. При 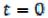 перемещение
перемещение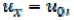 скорость , следовательно,
скорость , следовательно, 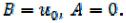
Выражение свободного движения возбужденной системы носит гармонический характер:
Введенную ранее величину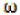 (число колебаний за время ) называют
(число колебаний за время ) называют
угловой собственной частотой колебаний, рад·с – 1:
Кроме угловой определяют линейную собственную частоту колебаний 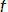
 , Гц:
, Гц:
При расчете низшей частоты собственных колебаний корпуса изолятора приведем схему корпуса с распределенной массой (рис. 4.9, а) к схеме с одной степенью свободы (рис. 4.9, б). Она состоит из безынерционного участка длиной l с приведенной изгибной жесткостью 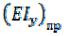 и сосредоточенной
и сосредоточенной
приведенной массы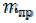 .
.
Массу последнего участка представим как сосредоточенную массу , приложенную в центре масс последнего участка. Массы всех остальных
участков – распределенные массы |
. |
Тогда приведенная масса |
|
где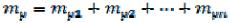 .
.
Коэффициент жесткости для участка с жесткой заделкой с одной сторо-
ны
27
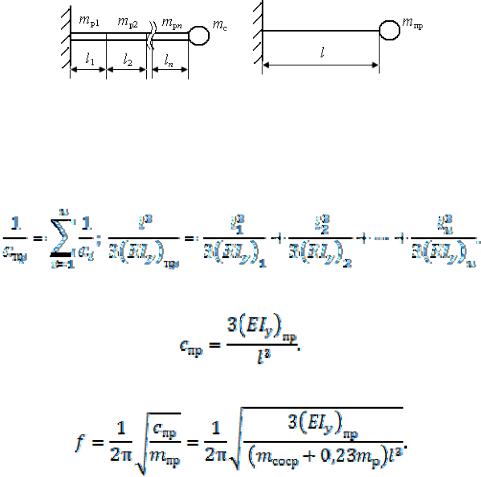
а |
б |
Рис. 4.9
Для схемы на рис. 4.9, а все участки являются последовательными, следовательно, приведенная жесткость
Коэффициент жесткости для схемы на рис. 4.9, б:
Тогда
Список литературы
1.Бегун П. И., Кормилицын О. П. Прикладная механика. – СПб.: Политехника, 1995.
2.Феодосьев В. И. Сопротивление материалов. – М.: Изд-во МГТУ им. Н. Э. Баумана, 2007.
28
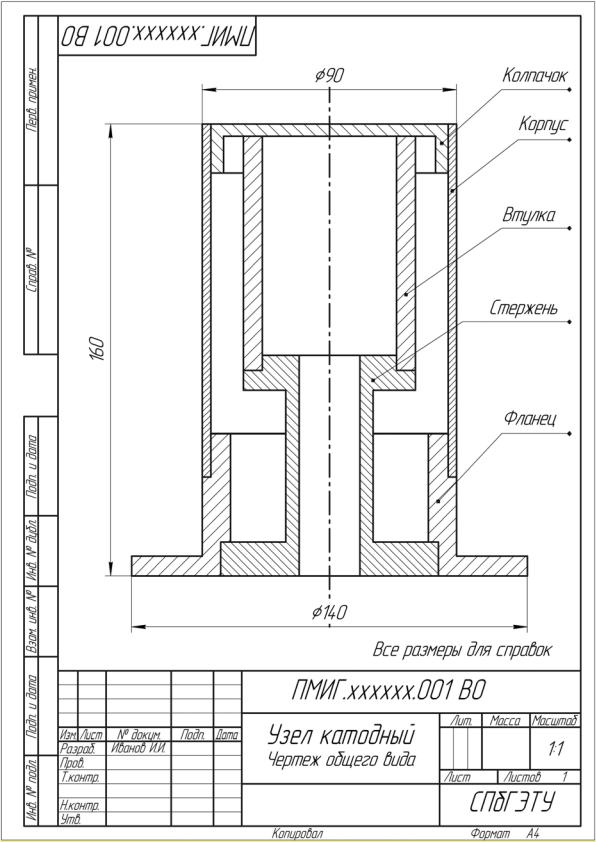
ПРИЛОЖЕНИЕ
Рис. П. 1
29

Рис. П. 2
30
