Sb96063

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

выделяем в числителе

2ax b k p dx , где

производную знаменател я

.pdf

Скачиваний:

Добавлен:

13.02.2021

Размер:

886.23 Кб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Для дробно-рациональных функций с действительными коэффициентами существует четыре вида простейших дробей, знаменатели которых есть натуральные степени всевозможных неприводимых делителей знаменателя исходной дробно-рациональной функции.

, A, a

x a

, A, a R.

(x a)

Ax B

A, B, a,b, c R, b2 4ac 0.

ax2 bx c

Ax B

A, B, a,b, c R, b2

4ac

(ax2 bx c)

При интегрировании дробно-рациональных функций необходимо придерживаться следующего алгоритма:

1. Если степень числителя больше или равна степени знаменателя (аналог неправильной дроби), то выделить ее целую часть.

Для выделения целой части можно пользоваться различными приемами. Наиболее надежный – разделить числитель на знаменатель «уголком». В результате деления получится многочлен, являющийся целой частью дробно-ра- циональной функции. Для оставшегося выражения степень числителя будет меньше степени знаменателя (аналог правильной дроби).

Пример 11. Выделить целую часть функции x3 2x 1 . x 2 1

Окончательно:	x3	2x 1	x	2x 1		.
		x2 1		x2	1

2. У полученной дробно-рациональной функции знаменатель нужно разложить в произведение степеней неприводимых многочленов. Методов разложения существует достаточно много. Наиболее распространенные: нахождение (в том числе и подбором) корней многочлена, метод группировки и использование формул сокращенного умножения.

3. Разложить дробно-рациональную функцию в сумму простейших дробей и проинтегрировать каждое из слагаемых. Методы разложения представлены в [1]. Разберем метод интегрирования каждой из простейших дробей для функций с действительными коэффициентами.

d (x a)

dx A

Aln

x a

(x a) 1

d (x a)

dx A

(x a)

Заметим, что в обоих случаях использовалось «подведение под знак дифференциала».

коэффициенты k и p подбираются таким образом, чтобы преобразованный числитель был равен исходному. Следующим шагом интеграл разбивается на

два интеграла 2ax b k p dx

2ax b k

dx .

bx c

Первый интеграл вычисляется «подведением под знак дифференциала»:

2ax b k

dx k

2ax b

d ax2 bx c

k ln

bx c

c1.

bx c

Во втором интеграле

выделяем в

знаменателе полный квадрат:

dx p

, где коэффициенты t и h подбираются таким

bx c

a x t

образом, чтобы преобразованный знаменатель был равен исходному. Далее в зависимости от знака перед h интеграл заменой переменных сводится или к 8- му или к 13-му табличным интегралам.

Ax B

Процесс взятия интеграла (ax2 bx c) dx отличается от предыду-

щего только тем, что после разделения на две части ко второму интегралу надо применить рекуррентную формулу:

	dx	I n , In	x	1	2n 3	In 1.
(x 2	a 2 )n		2a2 (n 1)(x2 a2 )n 1	a2	2n 2

Таким образом, зная, как берутся интегралы от всех простейших дробей, можно найти интеграл от любой дробно-рациональной функции.

1.2.5. Метод Остроградского

Работа с рекуррентными формулами вычислительно сложна. В качестве альтернативы рассмотрим метод Остроградского, позволяющий проинтегрировать произвольную дробно-рациональную функцию.

Рассмотрим f (x)dx , где	f (x)	Pn (x)	, где	Pn (x) и Qm (x) – много-
		Qm (x)

члены степеней n и m соответственно.

Пункты 1 и 2 приведенного выше алгоритма – выделение целой части, если подынтегральная дробь неправильная (т. е. n m ), и разложение знаменателя на множители – остаются без изменений. Соответственно, теперь будет рассматриваться ситуация, когда подынтегральная функция – правильная дробно-рациональная функция (т. е. n m ).

Разложение знаменателя на множители: Q

(x)

p s1

... p

sk qt1 ... qtr ,

где p a x b , q

2 4

0 ,

N , 1 i k,

1 j r. Если ввести дополнительное обозначение:

M p1 ... pk q1 ... qr ,

S ps1 1

... psk 1 qt1 1

... qtr

1. Тогда Q

M N , причем многочлен M

имеет степень v k 2r , а многочлен N имеет степень w m v .

Метод

Остроградского при

предположении

n < m

утверждает,

что

Pn (x)

Dv 1(x)

Gm v 1(x)

где Dv 1(x),Gm v 1(x) –

Q (x)

M N

многочлены с неопределенными коэффициентами степеней v 1 и m v 1 соответственно.

Обратите внимание! В правой части знаменатель выражения под интегралом при разложении на простейшие даст только простейшие дроби типов, интегрирование которых не требует применения рекуррентной формулы.

Остается найти коэффициенты многочленов Dv 1(x) и Gm v 1(x) . Для этого продифференцируем полученное равенство и получим:

P (x)

(x)

(x)N

(x)

(x) N G

v 1

m v 1

v 1

m v 1

Qm (x)

N 2

Затем нужно привести обе части равенства к общему знаменателю и перейти к равенству числителей. После этого остается раскрыть скобки, привести подобные слагаемые, и, опираясь на равенство многочленов, найти неопределенные коэффициенты.

x2 2x 6

Пример 12. Вычислить (x 1)(x 2)(x 4) dx .

Подынтегральная функция – правильная дробь, значит, выделять целую часть не нужно и первый шаг алгоритма пропускаем. Знаменатель дан в виде произведения неприводимых множителей, значит, и второй шаг пропускаем тоже. Следующим шагом необходимо разложить подынтегральную дробь на простейшие. Используем для разложения метод неопределенных коэффици-

ентов:

2x 6

(x 1)(x 2)(x 4) x

2 x

Приводим дроби в правой части к общему знаменателю, записываем ра-

венство для числителей и, сравнивая значения, найдем коэффициенты:

x2 2x 6

A(x 2)(x 4) B(x 1)(x 4) C(x 1)(x 2)

;

(x 1)(x

2)(x 4)

(x 1)(x 2)(x

x2 2x 6 A(x 2)(x 4) B(x 1)(x 4) C(x 1)(x 2) ,

при x 1

9 3A A 3,

при x 2

14 2B B 7,

при x 4

30 6C C 5.

Итак, исходная дробь представима в виде суммы простейших дробей сле-

дующим

образом:

2x 6

. В итоге

(x 1)(x 2)(x 4)

x 1

x 4

x2 2x 6

3ln

x 1

7 ln

x 2

(x 1)(x 2)(x 4)

x 1

x 2

x 4

5ln

x 4

Пример 13. Вычислить

dx .

(x 1)(x3

Подынтегральное выражение – правильная дробь, т. е. выделять целую часть не нужно.

Разложим знаменатель в произведение степеней неприводимых много-

членов: (x 1)(x3 1) (x 1)2 (x2 x 1) . Дискриминант второго множителя отрицателен, следовательно, перед нами – искомое разложение.

Выпишем разложение подынтегральной функции в сумму простейших дробей с неопределенными коэффициентами:

Cx D

(x 1)

x 1)

x 1

(x 1)

x 1

Приведем правую часть последнего равенства к общему знаменателю и перейдем к равенству числителей:

Cx D

(x 1)2 (x2

(x 1)2

x2 x 1

x 1)

x 1

A(x 1)(x2

x 1) B(x2 x 1) (Cx D)(x 1)

;

(x 1)2

(x2 x 1)

x A(x 1)(x2 x 1) B(x2 x 1) (Cx D)(x 1)2.

Найдем неопределенные коэффициенты. Можно использовать как подстановку некоторых значений (лучше корней знаменателя), так и равенство коэффициентов при одинаковых степенях.

Подставим x 1:1 3B B 13 ;

подставим x 0 : 0 A B D A D 13 .

Приравняем коэффициенты при соответствующих степенях: x3 : 0 A C A C,

x 2 : 0 B D 2C						1	D 2C D 2C					1		,
x 2 : 0 B D 2C							D 2C D 2C							,
					3						3
x : 1 B C 2D				2	C 2D			2	C 2(2C						1	) 0 3C C 0.
x : 1 B C 2D					C 2D				C 2(2C							) 0 3C C 0.
				3				3							3
Тогда D	1	, A 0.
Тогда D		, A 0.
3
									1								1
							x
Итак, разложение							x		3									3	.

			(x 1)2 (x2 x 1)							(x 1)2			x2				x 1

Запишем исходный интеграл в виде суммы интегралов:

(x 1)

x 1)

(x 1)

x 1

(x 1)

x 1

Вычислим полученные интегралы по отдельности:

dx	d (x 1)				1				c,

(x 1)2	(x 1)2						x 1
dx					dx							dx					1		dy
																y x
																	2
x2 x 1					1			1	3			1			3		2			3
x2 x 1			2		1			1	3			1		2	3				2	3
		x		2		x					(x		)			dy dx		y
		x		2	2	x		4		4	(x	2	)		4	dy dx		y		4

34 ( 43 y2 1) .

Сведем интеграл к табличному:

										t		2			y
				dy																	2				dt				2
				dy										3							2				dt				2	arctg(t) c.


	3		4		2							2											3 t 2			1			3
	3		4		2							2											3 t 2			1			3
		(		y			1)		dt							dy
		(		y			1)		dt			3				dy
4 3												3
Осталось вернуться к исходной переменной:
2										2								2								2				2					1
		arctg(t) c									arctg(									y)		c						arctg				(x				)	c.
																																			2
3										3								3								3				3
3										3								3								3				3
Итак,								x												1				2					2				1
													dx													arctg					(x			) c.
						(x 1)(x3														1													2
																			x					3					3
										1)									x					3					3
Пример 14. Вычислить																					x 3						dx .

																	x2 2x 2 2
																	x2 2x 2 2

Знаменатель подынтегрального выражения – степень квадратного трехчлена с отрицательным дискриминантом. Кроме того, подынтегральное выражение – правильная дробь. Таким образом, под интегралом – простейшая дробь 4-го типа. Вычислим этот интеграл двумя способами: при помощи рекуррентной формулы и методом Остроградского.

1-й способ.

Напомним рекуррентную формулу:

In ,

2n 3

In 1.

(x2 a2 )n

2a2 (n 1)(x2

a2 )n 1

2n 2

Преобразуем интеграл

x 3

2x 2 8

2x 2

dx 4

x2 2x 2 2

Вычислим интегралы-слагаемые по отдельности. Первое слагаемое – внесением под знак дифференциала:

2x 2

d (x2 2x 2)

2(x2

2x 2)

2x 2

Преобразуем второе слагаемое:

t x 1

2x 1

x 1

2x 2

dt dx

После преобразования интеграл приобрел вид, необходимый для приме-

нения

рекуррентной

формулы

( a 1,

n 2). И

применяя ее,

получим

arctg(t) c

(последний

интеграл

2 t 2

t 2 1 2

t 2 1

табличный).

Возвращаясь

исходной

переменной,

получим

arctg(t) c

x 1

arctg(x 1)

2 t 2 1

2 x 1 2

Итак,

x 3

x 1

arctg(x 1)

2(x

2x 2)

Упростив правую часть, получим итоговый ответ:

					2x		5
		x 3
		x 3		dx			2	2arctg(x 1) c.
x	2		2	dx	x2	2x 2		2arctg(x 1) c.
x		2x 2

2-й способ.

x2 2x 2 2 dx.

В этой задаче нет множителей вида pi

(в обозначениях описания метода

Остроградского), а

q x2 2x 2,

Тогда M N x2 2x 2 .

Применим основную формулу метода Остроградского:

x 3

c1x c2

d1x d2

dx, где c1,c2 , d1, d2 – не-

2x 2

x 2x

определенные коэффициенты.

Продифференцируем обе части:
	x 3								c1x c2					d1x d2

																			.
	x2 2x 2 2																		.
	x2 2x 2 2						x2 2x 2							x2 2x 2
Вычислим производную:
	x 3						c		x2 2x 2				2x 2 c x c							2				d x d							2
							1				x2 2x 2 2						1			2					1						2		.
	x2 2x 2 2										x2 2x 2 2												x2 2x 2										.
Приведем выражение к общему знаменателю:																																x2			2x 2
	x 3						c		x2 2x 2				2x 2 c x c							2			d x d							2		x2			2x 2
							1										1			2					1					2							.
											x2 2x 2 2																	x2 2x 2 2
	x2 2x 2 2										x2 2x 2 2																	x2 2x 2 2
Домножив обе части равенства на x2																2x 2 2 , получим:
	x 3 c		x	2		2x 2					2x 2	c x c					d x d									x		2
	x 3 c		x			2x 2					2x 2	c x c					d x d					2				x				2x 2 .
1													1			2		1				2
Раскроем скобки и приведем подобные:
	x 3 d x3				d		2	2d c x2					2c		2	2d 2d					2	x					2c 2c							2	2d	2	.
		1					2			1	1				2			1			2								1					2		2

Приравнивая коэффициенты при одинаковых степенях переменной в левой и правой частях, составим систему уравнений для неопределенных коэффициентов. Решая систему любым способом, найдем коэффициенты:

				d	0,									d1 0,
				1										c			2,
		d2 2d1 c1 0,														1	2,
									1,					d		2	2,
2c2 2d1 2d2									1,							2		5
	2c1 2c2 2d2 3,																	5	.
	2c1 2c2 2d2 3,														c2			2	.
																		2
Подставим найденные коэффициенты в исходное равенство:
			x 3								2x				5					2
			x 3								2x				2					2
							dx														dx.
	x2 2x 2 2						dx	x2 2x 2										x2 2x 2			dx.
Вычислим оставшийся интеграл:																				d x 1
			2			dx 2						dx					2			d x 1		2arctg (x 1) c.
		2				dx 2				x 1				2			2			2		2arctg (x 1) c.
	x	2	2x 2											2	1					2
	x		2x 2												1					x 1 1
																	5
Итак,					x 3						dx			2x 2						2arctg (x 1) c.
Итак,				x2 2x 2 2							dx		x2 2x 2							2arctg (x 1) c.
				x2 2x 2 2									x2 2x 2

Легко видеть, что применение метода Остроградского позволяет сильно упростить собственно интегрирование. При этом поиск неопределенных коэффициентов в разложении (т. е. фактически, решение линейной системы уравнений) присутствует во всех способах интегрирования дробно-рациональных функций.

Приведем еще один пример, демонстрирующий преимущества метода Остроградского.

Пример 15.

Вычислить x7 2x6 3x5 4x4 5x3 6x2 7x 8dx.

x2 1 4

При попытке вычислить данный интеграл при помощи рекуррентной формулы возникнет ряд технических сложностей.

Во-первых, при разложении в сумму простейших дробей придется решить систему порядка 8.

Во-вторых, рекуррентную формулу потребуется применить несколько раз (каждое ее применение понижает степень знаменателя как неприводимого многочлена на 1). После каждого такого применения нужно, вдобавок, приводить подобные. Заметим, что применять рекуррентную формулу приходится к каждому слагаемому последовательно, т. е. сначала – для 4-й степени знаменателя, затем для 3-й и т. д.

Вычислим данный интеграл при помощи метода Остроградского. Подынтегральное выражение – правильная дробь, знаменатель которой

уже разложен в произведение степеней неприводимых многочленов.

В наших обозначениях для метода Остроградского множителей вида pi

нет, множитель q

x2 1, t

Применив основную формулу метода Остроградского, получим:

2x6

3x5 4x4 5x3 6x2 7x 8

x2 1 4

Ax B

ax5

bx4 cx3 dx2 ex f

, где

A, B, a,b,c, d,e, f

– неопре-

деленные коэффициенты.

Продифференцировав обе части равенства, получим:

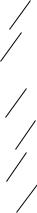
x7 2x6 3x5 4x4 5x3 6x2 7x 8

Ax B

x2 1

ex f

Вычислим производную:

x7 2x6 3x5 4x 4 5x3 6x 2 7x 8

Ax B

x 2 1

5ax 4 4bx3 3cx 2 2dx e x 2

1 3 6x x 2 1

ax5 bx 4 cx3 dx 2 ex f

x 2 1 6

Упростим правую часть:

2x6 3x5 4x4 5x3 6x2 7x 8

x2 1 4

Ax B

5ax4 4bx3 3cx2 2dx e x2 1 6x ax5 bx4 cx3 dx2 ex f

x2 1

Домножим равенство на x2

1 4 . Раскрыв далее скобки и приведя подоб-

ные слагаемые

правой

части,

получим следующее равенство:

x7 2x6 3x5 4x4 5x3 6x2 7x 8

x7 A x6 B a x5 3A 2b x4 3B 5a 3c x3 3A 4b 4dx2 3B 3c 5e x A 2d 6 f B e .

Составим систему уравнений для коэффициентов и решим ее:

1 A,		A 1,

2 B a,
2 B a,		B 15 4 ,
		a 7			,
3 3A 2b,		a 7			,
3 3A 2b,			4
	3B 5a 3c,	b 0,
4	3B 5a 3c,	b 0,
			16	3 ,
5	3A 4b 4d ,	c		3 ,
	3B 3c 5e,	d 1 ,
6	3B 3c 5e,	e 17			2
7 A 2d 6 f ,					2
7 A 2d 6 f ,						,
				4
				4
	B e.			7			.
8	B e.	f		7		6	.
						6

Подставим полученные коэффициенты в исходное равенство:

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.02.2021909.04 Кб13Sb95700.pdf
#
13.02.2021970.61 Кб17Sb95706.pdf
#
13.02.2021869.34 Кб10Sb95738.pdf
#
13.02.2021819.27 Кб3Sb95753.pdf
#
13.02.2021730.38 Кб10Sb95858.pdf
#
13.02.2021886.23 Кб1Sb96063.pdf
#
13.02.2021817.15 Кб2Sb96070.pdf
#
13.02.2021837.57 Кб8Sb96250.pdf
#
13.02.2021790.08 Кб1Sb96262.pdf
#
13.02.2021901.25 Кб3Sb96713.pdf
#
13.02.2021804.73 Кб4Sb96714.pdf