LS-Sb89586

Внекоторых случаях вычисляют c/a в кольце вычетов по модулю b.

Вэтом случае сначала можно вычислить 1/a, затем умножить результат на c в кольце вычетов по модулю b.

Уточняем, что умножить число в кольце вычетов по модулю b означает сначала умножить число, затем заменить результат его остатком от деления на b.

Пример. Можно решить уравнение 7x = 1 в кольце вычетов по модулю 9, то есть провести вычисление 1/7 в Z9 .

Вданном случае обозначим неизвестную величину как х. Тогда

x= 1/7 в Z9

7x 1 (mod 9)

7x – 1 9

7x – 1 = 9y

7x – 9y = 1

Получаем уже знакомую ситуацию – линейное диофантово уравнение. Можем его решить, но для первоначальной задачи достаточно найти всего одно значение х – например, подойдет x = 4. Заметим, что это число находится в пределах от 0 до 8, и поэтому может быть остатком при делении на 9.

Итак, ответ: x = 4.

Примечание. Ответ легко проверить умножением: 4 7 при делении на 9 дает остаток 1.

Если бы искали, например, 5/7 в Z9 , то сначала нашли бы 1/7 в Z9 (по-

лучив число 4), а затем домножили бы это число на 5 и взяли бы остаток при делении на 9 (остаток от деления 20 на 9 равен 2).

В этом случае ответ был бы равен 2.

Примечание. В задачах на нахождение выражений вида a/b в кольце вычетов по модулю c ответ всегда единственный, и является целым числом, находящимся в пределах от 0 до (c – 1).

В некоторых случаях деление невозможно, поскольку не каждое диофантово уравнение имеет решение. Например, уравнение 4x 1 (mod 10) не имеет решений, поскольку 4x – четное число, и при делении на 10 остаток будет четным.

11

1.18. Китайская теорема об остатках

Пусть m1, m2, ...,mn – попарно взаимно простые модули (то есть каждые два взаимно просты между собой), r1, r2, ...,rn – остатки. Тогда существует такой x, что

искомое число должно быть одновременно и четным, и нечетным, что невозможно.

Сначала, для примера, предположим, что у нас два модуля: m1 4,

m2 7, r1 1, r2 3.

Тогда представим искомое число в виде суммы двух чисел: одно дает остаток 1 при делении на 4 и кратно 7, а другое дает остаток 3 при делении на 7 и кратно 4.

Тогда сумма этих чисел даст искомые остатки.

В качестве первого числа можем взять 21, в качестве второго – 24. Сложив эти числа, получим 45.

Поскольку для единственности решения поставлено условие 0 x m1m2 ,

заменим число 45 его остатком от деления на 28, то есть числом 17.

Можно проверить, что оно действительно дает указанные остатки при делении на 4 и на 7.

Теперь – построение решения для китайской теоремы об остатках в общем виде.

Здесь будем строить его похожим образом, то есть в виде суммы n слагаемых, каждое из которых дает требуемый остаток по своему модулю, и при этом делится на остальные модули.

12

Первое слагаемое обеспечит остаток по первому модулю, второе – по второму, и так далее.

Обозначим сi m1m2...mn . mi

Из условия теоремы вытекает, что НОД (сi ,mi ) 1.

Следовательно, для каждого i существует di такое, что cidi 1(mod mi ). Найти такое di можно, если решить сравнение dici bimi 1(modmi ) (иначе говоря, найти частное решение диофантова уравнения).

виду, что будет взят остаток от деления данного числа на произведение m1m2...mn .

В самом деле, это число:

дает остаток r1 при делении на m1 (поскольку первое слагаемое дает указанный остаток, а остальные слагаемые делятся на m1),

дает остаток r2 при делении на m2 (поскольку первое слагаемое дает указанный остаток, а остальные слагаемые делятся на m2), и так далее.

1.19.Непрерывные дроби

иперевод рационального числа в конечную дробь

Определение. Непрерывной дробью называют дробь вида

Если эта дробь где-либо заканчивается, ее называют конечной непрерывной дробью. Конечные непрерывные дроби соответствуют рациональным числам.

Возможно и обратное действие: получение непрерывной дроби из рационального числа:

13

Обычно такую непрерывную дробь записывают в виде (2; 1, 1, 1, 2). Целая часть отделяется точкой с запятой.

Теперь покажем другой способ нахождения коэффициентов непрерывной дроби. Применим алгоритм Евклида к числам 21 и 8:

21 = 8 ∙ 2 + 5;

8 = 5 ∙ 1 + 3;

5 = 3 ∙ 1 + 2;

3 = 2 ∙ 1 + 1;

2 = 1 ∙ 2.

Обратите внимание на связь коэффициентов непрерывной дроби с неполными частными в алгоритме Евклида.

2.КОМБИНАТОРИКА

2.1.Задачи комбинаторики

1.Найти количество объектов, удовлетворяющих некоторым условиям.

2.Занумеровать элементы и построить алгоритм нахождения элемента по номеру и номера по элементу.

2.2.Правило произведения

Если А содержит n элементов, множество В содержит m элементов, то множество пар вида ai , b j , где ai А, b j B, содержит mn элементов.

Пример 1. Сколько существует способов поставить две шахматные ладьи на доску 8 8 так, чтобы они не «били» друг друга?

Решение. Есть 64 способа поставить первую ладью, и на каждый из них приходится по 49 способов поставить вторую ладью (поскольку первая ладья занимает одну клетку, и бьет при этом 14 клеток, то остается 49 клеток для второй ладьи). Таким образом, получим 64 49 вариантов расстановки двух ладей.

14

Но при этом каждая расстановка при таком подсчете будет сосчитана дважды, поскольку можно начать с первой ладьи, а можно – со второй. Поэтому найденное количество нужно разделить на 2.

Ответ равен (64 49)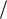2 1568.

Ответ. 1568.

Пример 2. Сколько существует трехзначных чисел, у которых все цифры различны?

Решение. Для первой цифры существует 9 вариантов, от 1 до 9. Когда ее выбрали, для второй цифры – тоже 9 вариантов, поскольку она не должна совпасть с первой. Когда выбрали первые две цифры, то для третьей осталось 8 вариантов.

По правилу произведения получим ответ: 9 9 8 648.

Ответ: 648.

2.3. Правило сложения

Идея рассуждения – разбить все варианты на группы, каждая из которых состоит из «одинаково устроенных» комбинаций.

Пример. Сколько существует способов поставить двух шахматных королей на доску 8 8 так, чтобы они не «били» друг друга?

Решение. В данном случае количество полей, которое «бьет» король, зависит от его положения на доске.

Если он в углу (4 варианта), то для второго короля свободны 60 полей, если у края доски (24 варианта), то свободны 58 полей, а если отстоит не в углу и не у края (36 вариантов), то свободны 55 полей.

Таким образом, получим 4 60 + 24 58 + 36 55 = 3612. Разделив это количество пополам (по той же причине, что в примере 1), получим 1806.

2.4. Перестановки

Перестановкой называют упорядоченный набор чисел 1, 2, 3, … n, возможно, переставленных в другом порядке – например, 3, 2, 1, 4, 5, 6, …, n.

Первый элемент перестановки можно выбрать n способами, тогда второй останется (n – 1) способ, на третий – (n – 2) способа, и так далее до заключительного элемента, для которого останется ровно один вариант.

Таким образом, количество перестановок равно n(n – 1)(n – 2) … 2 1 = n!

15

Примечание. В задачах по комбинаторике принято оставлять в ответе факториалы, степени, произведения, поскольку число в ответе задачи может оказаться большим и его вычисление может занять слишком много времени.

Пример. Сколько существует способов посадить 5 человек на 5 стульев по одному человеку на стул?

2.5. Размещения с повторениями

Размещение с повторениями – упорядоченный набор элементов, каждый из которых принадлежит данному множеству.

Если множество содержит n элементов, а наборы должны содержать k элементов, то каждый элемент можем выбрать n способами, всего k элемен-

тов, поэтому количество размещений с повторениями равно nk .

Пример. Сколько существует 4-значных чисел, все цифры в которых нечетны?

2.6. Размещения без повторений

Размещение без повторений – упорядоченный набор элементов, каждый из которых принадлежит данному множеству, и при этом все элементы набора должны быть различными.

Если множество содержит n элементов, а наборы должны содержать k элементов, то первый элемент можем выбрать n способами, второй (n – 1) способом, и так далее до элемента номер k, его можем выбрать (n – k + 1) способом. Поэтому количество размещений без повторений равно

Пример. Сколько существует 4-значных чисел, все цифры в которых нечетны и различны?

2.7. Сочетания

Cnk – число k-элементных подмножеств n-элементного множества (чита-

ется как «число сочетаний из n по k»).

Для нахождения количества сочетаний без повторений воспользуемся формулой для размещений без повторений.

16

Упорядоченных наборов k элементов из n существует n!/(n – k)! Если будем рассматривать неупорядоченные наборы, то каждый из них сосчитаем по k! раз.

Поэтому неупорядоченных наборов в k! раз меньше, чем упорядоченных.

Поэтому количество неупорядоченных наборов вычисляется по форму-

ле: n!/((n – k)!k!).

Пример. Сколько способов выбрать трех дежурных из 25 человек? Можно вычислять по формуле: 25!/(22!∙3!).

Можно и с помощью логических рассуждений: первого дежурного можно выбрать 25 способами, второго – 24 способами, третьего – 22 способами. Всего получаем 25 ∙ 24 ∙ 22 способа.

2.8.Переход к дополнению

Внекоторых случаях проще вычислить количество элементов, которые нам не подходят, а затем вычесть их количество из общего числа элементов.

Пример. Сколько существует 5-значных чисел, в которых есть хотя бы одна четная цифра?

2.9. Использование взаимно однозначного соответствия множеств

Пример. Найти количество всех подмножеств множества из N элементов. Решение. Обозначим каждое подмножество набором нулей и единиц, всего из N элементов. При этом на позиции номер i стоит 1, если элемент но-

мер i содержится в подмножестве, и 0, если не содержится в нем.

Тогда различных наборов 2N , поскольку на каждом из N мест может находиться или 0, или 1.

Количество подмножеств равно количеству наборов, поскольку подмножества и наборы нулей и единиц находятся во взаимно-однозначном со-

ответствии. Итак, количество подмножеств равно 2N . Ответ. 2N .

2.10. Принцип включений-исключений

Пример. Из 35 студентов 20 изучает английский язык, 15 – немецкий, 10 – французский, 7 – английский и немецкий, 5 – английский и французский,

17

4 – немецкий и французский, 3 – английский, французский и немецкий. Сколько студентов не изучает ни один из перечисленных языков?

Существует формула, называемая формулой включений-исключений, которая дает ответ на этот вопрос:

N0 N N1 N2 N3 N12 N13 N23 N123.

Что она означает? N – общее число студентов. N1 – число студентов, изучающих английский язык, N12 – английский и немецкий и т. д., N0 – число студентов, не изучающих ни один из перечисленных языков.

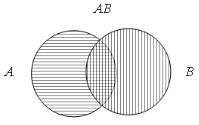
Для иллюстрации рассуждений такого типа используются рисунки, на-

зываемые диаграммами Венна (рис. 2.1).

Например, множество всех студентов в группе обозначено прямоугольником. Множество А обозначает всех студентов, знающих немецкий язык, множество В – всех студентов, знающих английский язык. Множество АВ (в центре рисунка) обозначает множество студентов, знающих оба иностранных языка, заштрихованная часть рисунка – студентов, знающих хотя бы один иностранный язык.

Наконец, незаштрихованная часть внутри прямоугольника – множество студентов группы, не знающих ни одного иностранного языка.

Пример. В группе из 25 человек 16 человек знает французский язык, 22 – английский, один не знает ни одного иностранного языка. Сколько студентов знают хотя бы один из двух иностранных языков?

Примечание. Часть данных в этой задаче лишняя, в задачах на формулу включения-исключения это бывает.

Задача. Секретарь рассыпал письма из конвертов, и обратно положил их наугад, по одному письму в конверт. Найти вероятность того, что хотя бы одно письмо попадет не в свой конверт.

Примечание. Ответ практически не зависит от количества писем и приближенно равен 1 – 1/ e , причем уже начиная с n = 6 – совпадение с точностью до 4 знаков после запятой.

18

2.11. Бином Ньютона

a b n n Ck an k bk

( ) n k 0

Для доказательства формулы можно рассмотреть выражение

(a + b) (a + b) … (a + b).

Подсчитаем, сколько раз в этом выражении встретится bk . Это выражение встретится столько раз, сколько существует способов выбрать k скобок, из

которых возьмем b, среди всех n скобок. А это количество способов равно Cnk . Из оставшихся (n – k) скобок выберем (n – k) множителей a. Таким обра-

зом, получим слагаемое Cnk an k bk . Так сделаем для k от 0 до n.

2.12. Свойства биномиальных коэффициентов

n

Cnk 2n . k 0

Доказательство. Подставим в бином Ньютона a = b = 1.

n

( 1)k Cnk 0. k 0

Доказательство. Подставим в бином Ньютона a = 1, b = –1.

2.13. Шары и перегородки

Рассмотрим задачу: сколько существует способов представить число n в виде суммы k натуральных слагаемых?

Можно представить ее так: набор из n шаров, расположенных в ряд, разделить на k частей, поставив (k – 1) перегородок.

В таком виде задача гораздо понятнее, поскольку следует выбрать (k – 1) мест из (n – 1) возможных, а количество способов сделать это извест-

но: Cnk 11.

Пример. Сколько существует способов представить 10 в виде суммы шести натуральных слагаемых?

Решение. Представим формулировку в таком виде: разбить цепочку из 10 шаров на шесть групп. Для этого достаточно разместить пять перегородок в 9 промежутках.

19

Это можно сделать C95 способами.

Ответ: C95 .

Можно усложнить задачу: сколько существует способов представить число n в виде суммы k целых слагаемых, каждое из которых не меньше m?

Эту задачу можно свести к предыдущей: для случая m = 1 решение задачи знакомо, а для общего случая для xi ≥ m (при i = 1, 2, …, k) можно сделать замену yi = xi – m + 1. Получим задачу для чисел y1, y2 , … yk , сумму которых можно вычислить:

y1+ y2 + … + yk = ( x1 – m + 1) + ( x2 – m + 1) + … + ( xk – m + 1) = = ( x1 + x2 + … + xk ) + k(–m+1) = n – km + k.

Таким образом, все числа yi натуральные, причем их сумма известна. Такая задача уже была решена.

2.14. Треугольник Паскаля

Рассмотрим задачу, сочетающую правило сложения и нахождение числа сочетаний: вывести рекуррентную формулу для подсчета биномиальных коэффициентов. Имеется в виду формула, позволяющая по коэффициентам разложения для степени n получить коэффициенты для степени n + 1.

Выделим из n элементов один и разобьем все k-элементные подмножества на два класса:

–содержащие выделенный элемент;

–не содержащие его.

Первых будет Cnk 11, так как один элемент уже выбран, и из оставшихся (n – 1) элементов надо выбрать еще (k – 1) элемент.

Вторых будет Cnk 1, так как один элемент запрещается выбирать, и надо

выбрать все k элементов из оставшихся (n – 1).

Так как любое подмножество (сочетание) принадлежит либо одному, либо другому классу и классы не пересекаются, получаем рекуррентную формулу:

Cnk Cnk 11 Cnk 1.

Процесс вычислений по этому рекуррентному соотношению можно представить в виде пирамиды, которая называется треугольником Паскаля

(рис. 2.2):

20