
LS-Sb90325
.pdf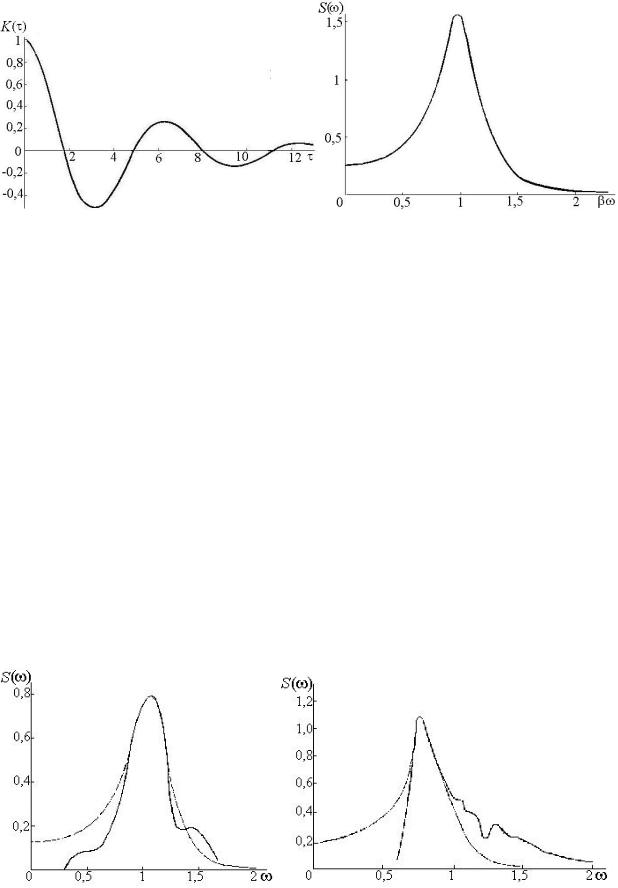
Рис. 1.6 Рис. 1.7
|
|
|
|
|
|
|
Таблица 1.1 |
|
Высота |
|
α рад/с |
|
|
β рад/с |
|
|
α/β |
волны, м |
|
|
|
|
|
|
|
|
αмах |
αсред |
αмин |
βмах |
βсред |
βмин |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1 |
0,560 |
0,374 |
0,138 |
2,240 |
1,745 |
1,250 |
|
0,215 |
|
|
|
|
|
|
|
|
|
2 |
0,394 |
0,265 |
0,136 |
1,573 |
1,239 |
0,905 |
|
0,214 |
|
|
|
|
|
|
|
|
|
3 |
0,316 |
0,214 |
0,111 |
1,266 |
1,003 |
0,740 |
|
0,213 |
|
|
|
|
|
|
|
|
|
4 |
0,274 |
0,185 |
0,096 |
1,094 |
0,667 |
0,640 |
|
0,213 |
|
|
|
|
|
|
|
|
|
5 |
0,246 |
0,166 |
0,086 |
0,982 |
0,777 |
0,572 |
|
0,213 |
|
|
|
|
|
|
|
|
|
6 |
0,224 |
0,151 |
0,078 |
0,898 |
0,709 |
0,520 |
|
0,213 |
|
|
|
|
|
|
|
|
|
7 |
0,207 |
0,140 |
0,072 |
0,828 |
0,654 |
0,480 |
|
0,214 |
|
|
|
|
|
|
|
|
|
8 |
0,194 |
0,131 |
0,068 |
0,774 |
0,612 |
0,450 |
|
0,214 |
|
|
|
|
|
|
|
|
|
9 |
0,184 |
0,123 |
0,063 |
0,734 |
0,578 |
0,422 |
|
0,213 |
|
|
|
|
|
|
|
|
|
10 |
0,177 |
0,119 |
0,061 |
0,706 |
0,555 |
0,404 |
|
0,214 |
|
|
|
|
|
|
|
|
|
11 |
0,171 |
0,140 |
0,058 |
0,684 |
0,537 |
0,390 |
|
0,213 |
|
|
|
|
|
|
|
|
|
12 |
0,166 |
0,112 |
0,057 |
0,664 |
0,522 |
0,380 |
|
0,3131 |
|
|
|
|
|
|
|
|
|
13 |
0,160 |
0,110 |
0,056 |
0,642 |
0,508 |
0,374 |
|
0,214 |
|
|
|
|
|
|
|
|
|
14 |
0,156 |
0,106 |
0,056 |
0,622 |
0,496 |
0,370 |
|
0,116 |
|
|
|
|
|
|
|
|
|
15 |
0,151 |
0,103 |
0,055 |
0,605 |
0,486 |
0,368 |
|
0,213 |
|
|
|
|
|
|
|
|
|
Рис. 1.8 |
Рис. 1.9 |
11

приближения, обеспечиваемая формулой (1.9), существенно ухудшается. Это обстоятельство следует иметь в виду, особенно при расчете тех систем, для которых главную роль играют составляющие энергетического спектра, соответствующие высоким или, наоборот, весьма низким частотам.
В частности, формула (1.9) дает завышенные оценки для гармоник энергетического спектра, близких к ω = 0. Заметим еще, что при движении судна частота возмущающих сил, действующих на него, может заметно отличаться от частоты воздействия волн на неподвижное судно, т. е. в формуле (1.9) нужно учитывать зависимость параметра β от скорости судна и от курса судна по отношению к гребням волн. Отношение α/β от скорости судна не зависит. Таким образом, в дальнейших расчетах будем использовать выражения (1.8) и (1.9). Морское волнение рассматривается как стационарный случайный процесс, который можно представить в виде суммы большого числа элементарных гармонических колебаний. Для таких процессов известны их статические характеристики: математические ожидания, дисперсии, спектральные плотности и т. п. При аппроксимации внешних воздействий, вызванных морским волнением, широко используют спектральную плотность мощности, в нормированной форме имеющую вид:
|
|
S (ω) = |
|
4α |
|
α2 + β2 |
|
|
. |
(1.10) |
||
|
|
|
π |
|
(α2 + β2 + ω2 )2 |
− 4β2 |
|
|||||
|
|
|
|
|
|
ω2 |
|
|||||
Для морского волнения также часто используется спектральная плот- |
||||||||||||
ность мощности в нормированной форме: |
|
|
|
|
||||||||
S (ω) = |
2α |
|
|
α2 |
+ β2 + ω2 |
|
|
|
|
(1.11) |
||
π |
|
(α2 + β2 + ω2 )2 − 4β2ω2 |
|
|
|
|||||||
|
|
|
|
|
|
|||||||
В формулах (1.10) и (1.11) приняты следующие обозначения: коэффициенты
β = 1, 44h3%−2/5 , α = 0,21β; ω = 
 β2 + α 2 – частота спектра; h3% – высота вол-
β2 + α 2 – частота спектра; h3% – высота вол-
ны 3 %-ной обеспеченности (в метрах). Значения h3% в соответствии с 9-
балльной шкалой оценки интенсивности волнения приведены в табл. 1.2 [9].
|
|
|
|
|
Таблица 1.2 |
|
Волнение, |
h3%, м |
Волнение, |
h3%, м |
Волнение, |
h3%, м |
|
баллы |
баллы |
баллы |
||||
|
|
|
||||
1 |
0…0,25 |
4 |
1,25…2,00 |
7 |
6,0…8,5 |
|
|
|
|
|
|
|
|
2 |
0,25…0,75 |
5 |
2,00…3,5 |
8 |
8,5…11 |
|
|
|
|
|
|
|
|
3 |
0,75…1,25 |
6 |
3,5…6,0 |
9 |
Более 11 |
|
|
|
|
|
|
|
12
Как было отмечено ранее, при движении судна частота сил внешнего воздействия на него, отличается от частоты сил внешнего воздействия на неподвижное судно. В связи с этим в формулах (1.10) и (1.11) необходимо учитывать зависимость параметра β от скорости и курса судна по отношению к направлению волн в случае морского волнения.
Сигналы со спектральными плотностями (1.10) и (1.11) можно получить из сигнала «белый шум», если пропустить его через фильтр, амплитудно-фа- зовая характеристика (АФХ) которого H(jω) определяется из условия
S(ω) = |H(jω)|2Sб.ш(ω), |
(1.12) |
где Sб.ш(ω) = 1.
«Белый шум» – это стационарный шум, время корреляции которого много меньше всех характерных времен физической системы. Его спектральные составляющие равномерно распределены по всему диапазону задействованных частот. «Белый шум» используется для измерения частотных характеристик различных линейных динамических систем, таких как усилители, электронных фильтров, дискретных систем управления и т. д. При подаче на вход такой системы «белого шума», на выходе получается сигнал, являющийся откликом системы на приложенное воздействие. Ввиду того, что амплитуд- но-фазовая частотная характеристика линейной системы есть отношение преобразования Фурье выходного сигнала к преобразованию Фурье входного сигнала, получить эту характеристику математически достаточно просто, для всех частот, для которых входной сигнал можно считать «белым шумом».
Во многих генераторах случайных чисел (как программных, так и аппаратных) «белый шум» используется для генерирования случайных чисел и случайных последовательностей. В природе и технике «чистый» «белый шум» (т. е. «белый шум», имеющий одинаковую спектральную мощность на всех частотах) не встречается (ввиду того, что такой сигнал имел бы бесконечную мощность), однако под категорию «белых» попадают любые шумы, спектральная плотность которых одинакова (или слабо различается) в рассматриваемом диапазоне частот.
При синтезе системы управления ГЭУ и последующем моделировании морского волнения удобно использовать спектры, параметры которых связаны с наблюдаемыми статистическими характеристиками и удовлетворительно согласуются с натурными измерениями, например:
13

|
|
|
|
|
Sη(ω) = |
4 |
ση2 |
|
|
|
|
α |
0 |
(α |
|
2 + β |
2 ) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
, |
(1.13) |
||||||
|
|
|
|
|
π |
|
ω4 + 2ω2 (α02 − β02 ) + (α02 |
+ β02 )2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
где σ2 |
= 0,143 (0,5h |
|
|
)2 |
|
– дисперсия волнения; h |
|
– высота волны 3%-ной |
|||||||||||||||||
|
|
η |
|
|
3% |
|
|
|
|
|
|
|
|
|
|
|
|
3% |
|
|
|
||||
обеспеченности (в |
метрах); |
α |
0 |
= 0,21β |
0 |
, |
β |
= 1, 44h−2/5 |
– |
коэффициенты; |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
3% |
|
|
|||
участвуют |
в спектре |
(для |
перехода |
|
от |
одной |
|
балльности к другой); |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ω |
max |
= |
|
β2 |
+ α2 – |
частота спектра. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В работе в качестве примера рассматривается волнение интенсивностью 6 баллов. Поэтому в соответствии с 9-балльной шкалой оценки интен-
сивности волнения (см. табл. 1.2): высота волны h3% = 6 м. Следовательно,
β = 1, 44h3%−2/5 = 0,703; ση2 = 0,143 (0,5h3% )2 = 1,287; α0 = 0,21β0 = 0,148.
Спектральной плотности (1.13) соответствует корреляционная функция:
R (τ) = σ2 e−α0 |
|
τ |
|
|
|
|
|
α |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
cosβ |
|
τ |
+ |
|
sin β |
|
τ |
|
. |
(1.14) |
||||
|
|
|
|
|
|
|
||||||||||
η |
η |
|
|
|
|
0 |
|
|
β0 |
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Учет изменения спектральных характеристик морского волнения в за-
висимости от скорости (vc) и направления (ε) движения судна осуществляется переходом к кажущимся частотам с помощью выражения [4]
ω = |
ω + kω2 |
; ω > 0 , |
(1.15) |
k |
|
|
|
где k = vc cos ε . g
Согласно формуле (1.15), при попутном волнении одному значению ε могут соответствовать три значения ω. Поэтому, учитывая неизменность дисперсии возмущения, результирующую спектральную плотность в этом случае можно записать в виде
S (ω ) = ∑ S (ω ) ∂ωi , |
(1.16) |
|||||
|
3 |
|
|
|
|
|
k |
|
i |
|
|
|
|
i=1 |
∂ω |
k |
|
|||
|
|
|
|
|||
где ω1,2,3 – решения выражения (1.16).
Моделирование спектров (1.16) достаточно сложно, поэтому выберем приближенный способ. Например, для спектральной плотности волнения (1.13) введем постановку:
β |
k |
= β |
0 |
+ kβ2 |
; α |
k |
= 0.21β |
k |
. |
(1.17) |
|
|
0 |
|
|
|
|
14

При этом с учетом выражения (1.17) спектр запишется в виде
′ |
4 |
2 |
α |
k |
(α |
k |
2 + β |
2 ) |
|
|
|
|
|
|
|
k |
|
|
|
||||
Sη (ωk ) = |
|
ση |
|
|
|
|
|
|
|
. |
(1.18) |
π |
ω4 + 2ω2 (αk 2 − βk 2 ) + (αk 2 |
|
|||||||||
|
|
+ βk 2 )2 |
|
||||||||
Сравнение спектров (1.13) и (1.18) показывает, что дисперсии у них одинаковые и, кроме того,
′ |
(1.19) |
ωmax [S (ωk )] = ωmax [S (ωk )]. |
Реализация на ЭВМ случайного процесса со спектральной плотностью вида (1.13) связана с использованием известного выражения
S (ω)вых = W(jω) W(–j ω) = |W(p)|2 S (ω)вх , |
(1.20) |
где S (ω)вых , S (ω)вх – спектральная плотность выходного и входного сигна-
лов; W(p) – передаточная функция фильтра. Передаточная функция W(p), или амплитудно-фазовая характеристика W(jω) = W(p) при р = jω формирующего фильтра, обеспечивает спектр заданного случайного сигнала. Если спектральная плотность входного сигнала будет соответствовать «белому шуму» в необходимом диапазоне частот, т. е. S (ω)вх = const, а |W(p)|2 будет равен спектральной плотности заданного сигнала, тем самым реализуется непрерывная случайная функция с заданными спектральными характеристиками.
Далее при синтезе системы управления ГЭУ и ее моделировании будем
рассматривать движение судна лагом к волне, когда угол ε равен 90°, при этом
спектр волнения будет соответствовать спектру морского волнения, действующему на неподвижное судно. Запишем передаточную функцию фильтра, квадрат модуля которой равен спектру морского волнения, для которого производится расчет оптимальной системы управления в общем виде:
Н( jω) = |
4ση2 |
α0 (α02 + β02 ) |
1 |
|
|
. |
(1.21) |
|
|
π |
|
( jω)2 + 2α0 ( jω) + (α0 |
2 + β0 |
2 ) |
|||
Переходя из частотной области во временную и принимая во внимание, что коэффициенты обратных связей оптимального закона управления не зависят от дисперсии случайного морского волнения, получим систему дифференциальных уравнений, описывающих случайное морское волнение:
vɺ= y; |
|
|
|
|
yɺ = −2α y − (α |
2 |
+ β |
2 )v + ω, |
(1.22) |
0 |
0 |
0 |
|
|
где ω – сигнал белого шума.
15

Ранее для волны 3%-ной обеспеченности равной 6 м, были рассчитаны
β0 = 0,703; α0 = 0,148; ση2 =1,287. Подставляя эти значения в (1.22), получим:
ɺ |
0 |
1 |
|
0 |
(1.23) |
||
x1 |
= |
− 0.516 |
− 0.296 |
х1 |
+ |
ω, |
|
|
|
|
|
|
|
||
|
|
|
|
0.401 |
|
||
где х1 – вектор переменных состояния внешнего воздействия с компонентами v, у. Выражение (1.23) далее будет использоваться при синтезе оптимальной системы управления ГЭУ при действии случайного морского волнения.
Как известно, передаточной функции, характеризующей реакцию системы на внешнее возмущение, соответствует линейное дифференциальное уравнение, описывающее ее движение под действием внешнего возмущения. Для передаточной функции (1.13) такое дифференциальное уравнение имеет вид
yp2 + 2α0 py + (α02 + β02 ) y = |
4ση2 |
α0 (α02 |
+ β02 ) |
|
|
|
|
|
x , |
(1.24) |
|
|
π |
|
|||
|
|
|
|
|
|
где у – выходной сигнал фильтра; х – входной сигнал типа «белый шум». |
|||||
Таким образом, моделирование на ЭВМ случайного волнового возмуще- |
|||||
ния, действующего на судно, связано с реализацией генератора «белого шума» и решением уравнения (1.24). Решим уравнение (1.24).
|
|
y( p2 + 2α0 p + (α0 |
2 |
+ β02 )) = |
4ση2 |
α0 (α02 |
+ β02 ) |
|
||||
|
|
|
|
|
|
x . |
(1.25) |
|||||
|
|
|
|
|
π |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ранее были рассчитаны для волны 3%-ной обеспеченности равной 6 м |
||||||||||
β |
0 |
= 0,703; α |
= 0,148; σ2 = 1,287. Подставляя эти значения в (1.25), получим: |
|||||||||
|
0 |
η |
|
|
|
|
|
|
|
|
||
|
|
|
y( p2 + 0.296 p + 0.516) = 0.401x . |
|
|
(1.26) |
||||||
Следовательно, передаточная функция фильтра |
|
|
|
|||||||||
|
|
|
W(p) = |
|
|
0.401 |
|
. |
|
|
|
(1.27) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
p2 + |
|
|
|
|
|
||||
|
|
|
|
0.296 p + 0.516 |
|
|
|
|
||||
Таким образом, случайное морское волнение будет представлено как фильтр, на входе которого действует сигнал вида «белый шум».
2.СИНТЕЗ СИСТЕМ УПРАВЛЕНИЯ ГЭУ
2.1.Синтез управления ГЭУ, оптимальных в свободном движении
Синтез автоматической системы ГЭУ производится по математической модели ГЭУ (1.1) без учета действия морского волнения (v):
16

ɺ |
|
|
−2 Tm |
|
n |
|
|
||
ɺ |
= |
−K |
T |
|
ia |
|
|
n |
a |
ɺ |
|
|
0 |
|
ud |
|
|
|
|
Ki Tm
Tm
−(KuKp +1) Ta 0
Ta 0
0 |
|
|
n |
|
0 |
K |
T |
|
i |
+ |
0 |
u |
a |
a |
|
|
|
−1 T |
|
ud |
KTB |
||
|
y |
|
|
|
|
Uy. (2.1)
Ty
Требуется определить закон управления, минимизирующий критерий качества:
∞
I = ∫ F (х, u, t) dt ,
|
0 |
|
|
где |
|
|
|
F = х |
тQ х + u |
тQ u , |
(2.2) |
|
1 |
2 |
|
где Q1, Q2 – диагональные матрицы размерностью п×п и т×т соответствен-
но, элементами которых являются весовые коэффициенты qli и q2j критерия качества. При выборе весовых коэффициентов будем исходить из предположения, что максимально допустимые значения всех переменных состояния должны вносить в суммарную ошибку (2.2) равный вклад. Исходя из этого, можно записать:
|
|
|
х1доп |
2 |
|
|
|
u1доп |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
q |
= |
q , |
q |
|
= |
|
q |
|
. |
(2.3) |
||||
|
|
|
|
|
|
|||||||||
1i |
|
хiдоп |
11 |
|
2i |
u jдоп |
|
21 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для нахождения соотношения между q11 и q22 будем предполагать, что полный вклад в суммарную ошибку максимально допустимых ошибок переменных состояния должен равняться вкладу максимально допустимых сигналов управления:
i=n |
|
|
|
j=m |
|
∑ q1i хi2доп = |
∑ q2 ju 2jдоп; |
(2.4) |
|||
i=1 |
|
|
|
j=1 |
|
подставляя выражения (2.3) в (2.4), получим |
|
||||
|
m u |
2 |
|
||
q11 = |
|
|
1доп |
q2i , |
(2.5) |
|
|
||||
|
n u2доп |
|
|
||
где q21 полагаем равным единице.
Оптимальный закон управления получим из решения матричного дифференциального уравнения Риккати.
17

Для синтеза оптимальных регуляторов линейных стационарных систем в пакете Matlab (Control System Toolbox) имеется функция
[K P e] = lqr (A, B, Q, S, N),
с помощью которой осуществляется синтез непрерывного регулятора. Функция lqr вычисляет матрицу коэффициентов регулирования K cо
среднеквадратичным функционалом качества:
I = ∞[x тQx + u тSu + 2x тNu]dt
∫ ,
0
при этом вычисляются матрица P, являющаяся решением уравнения Риккати и собственные значения e матрицы (A – BK).
Если задать K = lqr (A, B, Q, 1), что означает S=1, а N=0, то получим только матрицу коэффициентов регулирования. Рассмотрим численный при-
мер с исходными данными: ku=196; ktv=59; Ty=0.012; Tm=1.0; ki=0.1156; Ta=0.3; kv=80; kp=0.05; kn=1100.
Матрица А имеет следующий вид:
−2 T |
K |
|
T |
0 |
|
|
|
−K |
m |
i |
|
m |
|
|
|
T |
−(K K |
p |
+ 1) T K T |
, |
|||
|
n a |
u |
|
a u |
a |
|
|
|
0 |
|
0 |
−1 T |
|
|
|
|
|
|
|
|
|
y |
|
матрица В –
|
|
0 |
|
|
|
|
|
0 |
|
, |
|
|
|
|
|
||
|
KTB Ty |
|
|
||
|
|
|
|
|
|
матрица Q – |
|
|
|
|
|
q |
0 |
|
0 |
|
|
|
11 |
q22 |
|
|
|
|
0 |
|
0 |
. |
|
|
0 |
0 |
|
q33 |
|
|
|
|
|||
Задание для расчета матрицы коэффициентов закона регулирования с использованием функции lqr в Matlab имеет вид:
A=[-2/Tm ki/Tm 0; -kn/Ta -(ku*kp+1)/Ta ku/Ta; 0 0 -1/Ty]; B=[0; 0; ktv/Ty];
q11=1/3*(18.0/161*1)^2; q22= (161*1/2795)^2*q11; q33= (161*1/922)^2*q11;
Q1= [q11 0 0; 0 q22 0; 0 0 q33]; K= lqr(A, B, Q1, 1),
18
где значения n=161, ia=2798, ud=922, получены из решения структурной схемы ГЭУ в Matlab/Simulink (рис. 1.3). Необходимо отметить, что процесс определения коэффициентов закона регулирования, удовлетворяющих требованиям, предъявляемым к точности и качеству регулирования системы управления, носит итеративный характер. Приведенный расчет коэффициентов критерия оптимальности является первой итерацией. После проведения моделирования системы управления ГЭУ с полученным законом управления требования по точности стабилизации частоты вращения ГЭД не удовлетворяются. На третьей итерации были рассчитаны коэффициенты критерия оптимальности при следующих численных значениях: q11=1/3*(18.0/161*0.1)^2;
q22= (161*0.1/2795)^2*q11; q33= (161*0.1/922)^2*q11.
В результате получаем матрицу коэффициентов закона регулирования
К=[0.3885 0.0028 0.0170].
2.2.Синтез оптимальных автоматических систем управления ГЭУ
сучетом случайных внешних воздействий
Задача синтеза оптимальных автоматических систем управления с учетом случайных внешних воздействий решена в работе [1]. Решение задачи синтеза оптимальных автоматических систем управления с учетом гармонических внешних воздействий, изложено в работе [2]. Методы решения, разработанные в этих источниках, достаточно трудоемки и плохо приспособлены для использования современных компьютерных технологий. Далее будет применяться методика (см. [3]), которая позволяет провести синтез и исследование системы управления ГЭУ в пакете Matlab (Simulink).
При синтезе таких систем будем предполагать, что случайные внешние воздействия являются случайными процессами, обладающими свойствами стационарности и эргодичности. Для таких процессов обычно известны их статистические характеристики: дисперсии, спектральные плотности и т. п. При аппроксимации внешних воздействий, вызванных морским волнением и ледовым воздействием, широко используют [3] спектральную плотность мощности, в нормированной форме имеющую вид
S (ω) = |
4α |
|
|
|
α2 + β2 |
|
|
. |
(2.6) |
π |
|
(α2 |
+ β2 |
+ ω2 )2 |
− 4β2 |
|
|||
|
|
ω2 |
|
||||||
19

Для морского волнения часто используется спектральная плотность мощности в нормированной форме
S (ω) = |
2α |
|
|
α2 + β2 + ω2 |
|
. |
(2.7) |
π |
|
(α2 |
+ β2 + ω2 )2 − 4β2 |
|
|||
|
|
ω2 |
|
||||
В формулах (2.6) и (2.7) приняты следующие обозначения: β = 1, 44h3%−2/5 , α = = 0,21β; ω = 
 β02 + α02 – частота спектра; h3% – высота волны 3 %-ной обес-
β02 + α02 – частота спектра; h3% – высота волны 3 %-ной обес-
печенности (в метрах).
Ранее отмечалось, что при движении судна частота сил внешнего воздействия, действующих на него, отличается от частоты сил внешнего воздействия, действующих на неподвижное судно. В связи с этим в формулах (2.6) и (2.7) необходимо учитывать зависимость параметра β от скорости и курса судна по отношению к направлению движения волн в случае морского волнения. В работе будет использоваться спектр морского волнения (2.6).
Силы внешних воздействий в виде морского волнения и ледового воздействия практически трудно измерить в процессе управления. Это обстоятельство делает невозможным предварительное определение оптимального движения и реализацию его с помощью программного управления. В этих условиях необходимо производить синтез оптимальных автоматических систем, т. е. определять оптимальный закон управления, который реализовывал бы оптимальное движение, используя информацию только о текущих значениях переменных состояния системы и о вероятностных характеристиках внешних сил. Оптимальный закон управления, использующий информацию о текущих значениях переменных состояния системы, может быть получен из решения матричного дифференциального уравнения Риккати.
Объект управления (ГЭУ) описывается векторным линейным дифференциальным уравнением
ɺ |
(2.8) |
x = Фх + Gu , |
где х – n-мерный вектор; u – m-мерный вектор управления; Ф, G – матрицы размерностью п×п и т×т соответственно. Требуется определить закон управления, минимизирующий критерий качества:
∞
I = ∫ F (х,u,t)dt ,
0
где
F = х |
тQ х + u |
тQ u . |
(2.9) |
|
1 |
2 |
|
20
