
Sb98038
.pdf
Выразив вертикальное ускорение через угловое ускорение стержня, получим, суммируя вертикальные проекции тангенциального и центростремительного ускорения:
aверт 2l cos 2 sin .
Учитывая, что в данном представлении движение стержня описывается вращением вокруг ЦМ, для углового ускорения получим:
l |
F |
cos ml2 |
. |
|
2 |
||||
верт |
12 |
|
В горизонтальном положении (θ = 0) получим окончательно для вертикальной составляющей силы давления
Fверт mg4
Сила –Fверт представляет собой составляющую силы, действующую
вертикально вниз на ось вращения стержня.
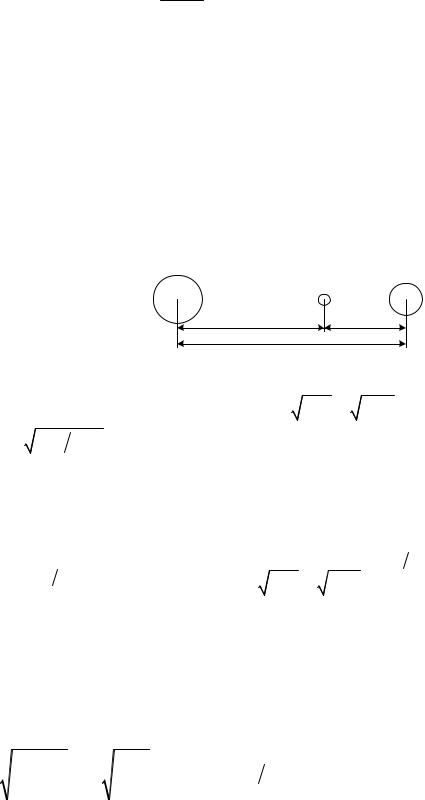
30. Второй закон Ньютона для центра масс (ЦМ) гантели: dpc  dt 2mg N. Поскольку силы, действующие на стержень, при любом его положении направлены вертикально, dpcx
dt 2mg N. Поскольку силы, действующие на стержень, при любом его положении направлены вертикально, dpcx  dt 0. Следовательно, ЦМ гантели при ее движении будет двигаться по вертикали.
dt 0. Следовательно, ЦМ гантели при ее движении будет двигаться по вертикали.
По закону сохранения энергии и теореме Кенига имеем
l |
|
|
|
|
l |
|
|
|
|
2 |
α |
|
|
|
2 |
C |
|
|
|
N |
|
|
l |
|
vcc |
v |
|||
2 |
||||
r |
||||
2mg |
||||
x
|
|
2mg |
l |
1 cos |
Jc 2 |
|
2mvc2 |
, |
(1) |
|
|
|
2 |
||||||
|
|
2 |
|
|
2 |
|
|
||
где Jc ml2 |
4 ml2 |
4 ml2 |
2 – момент инерции гантели относительно ЦМ; |
||||||
vc vsin l |
2 sin – скорость ЦМ, когда ось гантели составляет угол α |
|||||||||
с вертикалью. Подставив указанные соотношения в (1), получим: |
|
|||||||||
|
( |
) |
=ω |
2 |
( |
2 |
α |
) |
. |
(2) |
|
4g 1-cosα |
|
|
l 1+sin |
|
|
||||
31

Отсюда выразим величину |
|
|
|
2 |
4g 1 cos |
|
(3) |
l 1 sin2 |
Продифференцировав уравнение (2) по времени и сократив на величину ω, используя (3), можно определить угловое ускорение гантели в представляющий интерес момент времени (эту операцию рекомендуем провести самостоятельно):
|
|
|
|
1 cos |
2 |
|
|
||||
|
2g sin 1 |
|
|
|
(4) |
||||||
l |
|
sin |
2 |
|
2 |
|
|
||||
|
|
|
|
|
|||||||
|
|
1 |
|
|
|
|
|
|
|||
Наконец, запишем уравнение вращательного движения гантели относительно ЦМ: Jcε Mc. Здесь Mc r N . В проекции на ось, направленную по ε, имеемMc N l 2 sin . В итоге находим силу, действующую на ган-
2 sin . В итоге находим силу, действующую на ган-
тель со стороны плоскости, в тот момент, когда ось гантели составляет угол α с вертикалью:
|
1 |
|
cos |
2 |
|
|
||||
N 2mg |
1 |
|
|
(5) |
||||||
|
sin |
2 |
|
2 |
||||||
|
|
|
||||||||
|
1 |
|
|
|
|
|
||||
Искомая сила по величине по третьему закону Ньютона совпадает с (5). Для проверки полученного результата полезно рассмотреть предельные
значения угла α. При α = 0 |
(исходное положение гантели) N 2mg. При α = π/2 |
N mg, т. е. при падении |
гантели на плоскость на каждый из шариков ганте- |
ли действует сила, равная |
mg. |
31. Это задача на движение тела с переменной массой. Из уравнения Мещерского m ddtv F dmdt u в отсутствие внешней силы F, действующей на тело, следует формула Циолковского m m0 exp v u , где m – масса тела,
u , где m – масса тела,
движущегося со скоростью v; m0 |
– масса тела при v = 0; u – скорость относи- |
||||||||
|
|
|
|
|
E = mv2 |
= m0 v2e- |
v |
||
тельного движения выбрасываемых |
частиц. Тогда |
u |
. |
||||||
|
|
|
|
|
к |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
||
Определив экстремум функции |
dE |
|
v 2u. Таким образом, |
||||||
|
к 0 , найдем |
||||||||
|
|
|
dt |
|
|
|
|
|
|
E |
2m u2e 2. |
|
|
|
|
|
|
|
|
кmax |
0 |
|
|
|
|
|
|
|
|
32
32. Потенциальная энергия взаимодействия двух шаров (или материаль-
ных точек) вычисляется по формуле U m1rm2 , где r – расстояние между
центрами шаров. При этом аддитивная постоянная в выражении для потенциальной энергии полагается равной нулю при бесконечном расстоянииr между телами. При таком выборе нулевого значения потенциальная
энергия двух шаров (или материальных точек) всегда будет отрицательна, причем она возрастает с увеличением расстояния.
Потенциальную энергию аппарата как функцию его расстояния до центра Луны можно записать в виде
U x mMЗ |
mMЛ , |
|
|
L x |
x |
|
|
где МЗ = 6,0·1024 кг – масса Земли; |
З |
m |
Л |
М = 7,3·1022 кг – масса Луны; m – масса |
|
||
|
|
|
|
Л |
L x |
|
x |
аппарата; L = 3,8·108 м – расстояние меж- |
|
||
L – x |
LL |
||
ду центрами Земли и Луны. Функция U(x) |
|
|
|
|
|
|
имеет максимум при x |
|
|
|
L |
, равный Umax |
m |
MЗ |
MЛ 2 |
|
|
|
|
|
|
|
|
|
||
1 |
|
MЗ MЛ |
|
L |
|
||||
|
|
|
|
|
|||||
Если кинетическая энергия Т аппарата в этой точке равна нулю, то вблизи поверхности Луны она равна Tmin RЛ Umax U RЛ , где Rл = 1,7 · 105 м – радиус Луны. При этом скорость аппарата у поверхности Луны равна
2 |
1 2 |
|
|
M |
|
|
M |
|
|
MЗ |
МЛ |
2 |
1 2 |
|
|
|
З |
|
|
|
|
|
|||||||||
v vmin |
|
Umax U RЛ |
2 |
|
|
|
Л |
|
|
|
|
|
|
||
|
|
R |
R |
|
L |
|
|
||||||||
m |
|
|
L |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
Л |
|
Л |
|
|
|
|
|
|
|
Полезно упростить это выражение, используя разложение в ряд по малому параметру z RЛ L 10 3. Проделайте это самостоятельно (воспользо-
L 10 3. Проделайте это самостоятельно (воспользо-
вавшись формулой 1 z n 1 nz ) и получите выражение
|
|
M |
|
|
М |
З |
|
R |
|
|
v |
2 |
|
Л 1 |
|
|
|
Л |
|
7,5 км с. |
|
R |
М |
|
L |
|||||||
min |
|
|
|
Л |
|
|
|
|||
|
|
Л |
|
|
|
|
|
|
||
Убедитесь, что относительная погрешность в расчетах по точной и приближенной формулам не превышает 0,03 %.
33

33. Воспользуемся теоремой Гаусса для гравитационного поля:g dS 4 Gm, где g – напряженность гравитационного поля; G – грави-
S
тационная постоянная; m – масса внутри поверхности, по которой ведется интегрирование в левой части. Возьмем замкнутую поверхность в виде сферы с центром в центре Земли, радиусом r ≤ RЗ. Тогда из соображений сим-
метрии получим: 4 r2g 4 G 43 r3, где ρ – плотность Земли, равная
M  V 3M
V 3M 4 RЗ3 . Здесь M и RЗ – масса и радиус Земли соответственно.
4 RЗ3 . Здесь M и RЗ – масса и радиус Земли соответственно.
В итоге напряженность гравитационного поля внутри Земли линейно зависит от расстояния от центра вдоль радиального направления: g =-4πGr 3, где
3, где
знак «минус» указывает на то, что вектор напряженности g направлен к центру Земли. Тогда величина гравитационной силы, действующей на тело мас-
сой m, на расстояниях r ≤ RЗ равна F 43 G mr.
Воспользуемся теоремой, согласно которой работа всех сил, действующих на тело (в данном случае – только гравитационной силы), равна прира-
R 4 |
Gmrdr |
mv2 |
(Полагаем, |
|
щению кинетической энергии тела, т. е. |
|
0 |
||
0 |
3 |
|
2 |
|
что барон на ядре достигает поверхности Земли с пренебрежимо малой скоростью.) Интегрируя, получаем: v0 4  3 G R2 MG
3 G R2 MG R. Учитывая, что
R. Учитывая, что
MG gЗR2, где gЗ – ускорение свободного падения у поверхности Земли, окончательно получим: v0 gЗR 7,9 км с. (Совпадает с первой космической скоростью.)
с. (Совпадает с первой космической скоростью.)
Другой вариант решения. Рассмотрим движение барона на ядре от центра Земли к поверхности как четверть колебания тела от положения равновесия до крайнего положения под действием квазиупругой силы
F kr, где |
|
k 4 3 G m |
(см. ранее). В данном случае |
амплитуда |
|||
колебаний r |
0 |
= R. Тогда |
v |
r |
k m R 4 3 G R2 |
MG R |
|
|
|
|
0 |
0 |
|
|
|
|
gЗR 7,9 км с. |
|
|
|
|
||
34

34. Пусть М – масса планеты, ρ – ее плотность, R – радиус. Достаточно рассмотреть послойное разрушение планеты, когда тонкий слой толщиной dr удаляется с ее поверхности. При этом затрачивается энергия, эквивалентная потенциальной энергии взаимодействия этого слоя с массой оставшейся части планеты. При этом
dW Mr |
dmr |
4 |
r3 4 r2dr |
|
16 |
2 2r4dr. |
|
r |
3 |
r |
|
3 |
|
В результате полная энергия, затраченная на разрушение планеты:
0 |
|
16 2 |
2 |
4 |
|
16 2 |
|
2 |
R5 |
|
3 |
|
M 2 |
|
W |
|
3 |
|
r |
dr W |
|
|
|
|
|
|
|
R |
|
3 |
|
5 |
5 |
|||||||||||
R |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
35. 1. В случае кругового движения сила притяжения является центростремительной силой, таким образом, для центростремительного ускорения имеем:
v2 dU 3Kr2. r dr
Подставив радиус орбиты, получим:
v 3ka3 .
Далее элементарно находим кинетическую энергию частицы и ее момент импульса:
W |
3 Kma3; |
L ma2 |
3Ka. |
к |
2 |
|
|
2. Для нахождения периода обращения следует использовать связь между периодом и угловой скоростью движения частицы, в результате получим:
T 2
3Ka
36. Обе трубы горизонтальны; следовательно, каких-либо изменений потенциальной энергии жидкости нет. В сечении С кинетическая энергия еди-
ничного объема жидкости равна vC2  2 (ρ – плотность жидкости), а в сече-
2 (ρ – плотность жидкости), а в сече-
нии В – vB2  2. Дано, что vВ = 20 см/с. Скорость vС можно найти из закона сохранения массы:
2. Дано, что vВ = 20 см/с. Скорость vС можно найти из закона сохранения массы:
vC vB SB 120 см с.
SC
35

С |
Рp |
|
C |
|
|
|
СC |
|
A |
РpВB |
B |
А |
|
В |
h |
|
|
Разность давлений в сечениях В и С находим из закона сохранения энергии для единичного объема воды:
pB pC 12 vC2 12 vB2 7000 г см с2 ;
см с2 ;
она должна быть равна разности давлений в трубках манометра, подсоединенных к В и С, которая определяется по высоте водяного столба
воды 1 г см3 между уровнями:
см3 между уровнями:
рт воды gh pB pC .
Следовательно, h 5,5 мм.
37. За время dt вытечет вода объемом dV v dt, где v – скорость вытекания струи. При этом уровень воды понизится на dh dV  S . Отсюда нахо-
S . Отсюда нахо-
дим v S dh dt |
dh |
dt 0 . |
Подставив это выражение в известную |
||||||||
формулу |
Торричелли |
v |
2gh, |
получим дифференциальное |
уравнение |
||||||
dh dt 2gh S , |
решение |
которого |
с |
заданным начальным |
условием |
||||||
h |t 0 h0 |
есть h(t)=( |
|
h0 -σt |
g |
2 S). |
Время вытекания определяется |
|||||
условием h t0 0 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
|
|
2h0 |
|
|
|
|
|
|
|
|
|
|
S |
g |
|
|
38. Энергия маятника |
|
|
|
|
|
|
|
||||
|
|
E |
ml 2 |
mgl cos |
mgl cos , |
|
|||||
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
36

где φ – угол отклонения нити от вертикали; φ0 – максимальный угол отклонения. Вычислив период как учетверенное время прохождения интервала углов от нуля до φ0, находим:
T 4 |
|
l |
|
φ0 |
dφ |
|
|
|
|
|
|
|
|
2 |
|
|
|
l |
φ0 |
|
|
|
dφ |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2g |
|
|
cosφ cosφ0 |
|
|
|
|
g |
|
|
|
2 φ0 |
|
|
|
2 φ |
|
||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
sin |
sin |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
||||
Подстановкой sin φ |
sin φ0 |
sin ξ этот интеграл приводится к виду |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
T |
4 |
|
|
|
|
|
K sin |
0 |
|
, |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π 2 |
|
|
|
|
dξ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
K k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
sin |
0 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
0 |
|
1 k |
sin |
|
ξ |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
– так называемый полный эллиптический интеграл |
|
первого |
|
рода. При |
||||||||||||||||||||||||||||||||||||
sin 0 2 0 |
2 1 (малые колебания) разложение функции K(k) дает: |
|||||||||||||||||||||||||||||||||||||||
|
|
π 2 |
|
|
|
dξ |
|
|
π 2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
φ2 |
|
||||||||||||
K k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
k2 sin2 ξ dξ |
|
|
|
1 |
|
|
0 |
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
0 |
|
|
1 k2 sin2 ξ |
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
16 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
В результате получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
T 2 |
|
l |
1 |
1 |
2 |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Первый член этого разложения отвечает известной элементарной формуле. (Полезно самостоятельно провести выкладки, приводящие к этому ре-
зультату.)
Возвращаясь к вопросу в задаче, находим
T T T0 |
|
|
1 |
2 |
|
1 |
|
2 |
0,017 1,7 %. |
||
|
|
|
|
|
|
|
|||||
T0 |
|
16 |
0 |
|
16 |
6 |
|
||||
|
|
|
|
|
|
||||||
39. Данная задача – о движении системы, состоящей из двух взаимодей-
ствующих частиц (задачадвухтел). Как известно, эта задача сводится к решению
задачи о движении одной точки с массой m |
m1m2 |
|
(величина m называется |
|
m m |
||||
|
|
|||
|
1 |
2 |
|
|
37

приведенной массой) в заданном внешнем поле U(r) (энергии упруго деформированной пружины). Следовательно,
T 2 |
m1m2 |
|
2 |
3m |
|
3m |
|
||
m m |
k |
4k |
k |
||||||
|
|
|
|
||||||
|
1 |
2 |
|
|
|
|
|
|
|
40. 1. Пусть x – расстояние, на которое брусок смещается из положения равновесия. Из уравнения движения
Mx k1 k2 x 0
определяем частоту колебаний |
|
|
|
k1 k2 |
|
|
M |
|
2. Новая система, масса которой m + М, имеет частоту колебаний
k1 k2
M m
3.Пусть v1 – скорость бруска, с которой он проходит положение равно-
весия. В соответствии с законом сохранения энергии имеем
1 Mv2 |
|
1 |
k |
k |
2 |
A2 |
, |
(1) |
|
2 |
1 |
|
2 |
1 |
|
|
|
|
|
где А – амплитуда колебаний. Запишем закон сохранения импульса
Mv1 M m v2, (2)
где v2 – скорость бруска с прилипшим к нему грузом m. Выразим переход кинетической энергии в потенциальную в виде
1 |
M m v2 |
|
1 |
k |
k |
2 |
B2. |
(3) |
2 |
2 |
|
2 |
1 |
|
|
|
Исключив из (1)–(3) v1 и v2, найдем соотношение между новой амплитудой колебаний В и амплитудой А:
|
M |
|
B |
|
A. |
M m |
||
41. Выпишем уравнение движения стержня, который совершает колеба-
тельное движение, оставаясь в вертикальной плоскости, относительно оси, про-
ходящей через центр чашки. Имеем: J d 22 mgr sin . В этом выражении J – dt
момент инерции стержня относительно точки центра сферы, вычисляемый по
38

|
1 |
2 |
2 |
1 2 |
æ |
2 |
|
l |
2 |
ö |
æ |
2 |
|
l |
2 |
ö |
|||
|
ç |
|
|
÷ |
ç |
|
|
÷ |
|||||||||||
теореме Штейнера: J = |
|
|
ml |
+mr = |
|
|
ml |
ç |
|
- |
|
|
÷ |
ç |
|
- |
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
||||||||||
12 |
12 |
+mçR |
|
|
|
÷ |
=mçR |
|
6 |
÷. |
|||||||||
|
|
|
|
ç |
|
|
4 ÷ |
ç |
|
|
÷ |
||||||||
|
|
|
|
|
|
|
|
è |
|
|
|
|
ø |
è |
|
|
|
|
ø |
При малых колебаниях sin α@α. В результате приходим к уравнению гармо-
|
|
æ |
2 |
|
|
l |
2 |
ö |
|
2 |
α |
|
|
2 |
|
l |
2 |
|
|
|
|
|
|
|
|
ç |
|
|
|
÷d |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
ç |
|
- |
|
|
÷ |
|
|
|
|
+ g |
R |
|
- |
|
|
α=0 |
, |
из которого |
|||
нических колебаний стержня çR |
|
6 |
÷ |
|
|
2 |
|
4 |
|||||||||||||||
|
|
ç |
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
è |
|
|
|
|
|
ø dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
R2 -l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
следует: T =2π |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g R2 -l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
42. Поскольку шарик катится без скольжения, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
справедливо соотношение vc r R r d , |
|
|
|
|
|
|
φ |
R – r |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
R |
|
ω r |
|||
из которого находим связь между угловой ско- |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
vс |
||||||||||||||||
ростью ω вращения шарика вокруг оси и угло- |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
вой скоростью d dt его движения по поверхности полусферы: |
|
|
|
||||||||||||||||||||
|
|
ω= |
R -r |
dφ |
|
|
|
|
|
|
|
|
(1) |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
r |
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
||
По закону сохранения энергии имеем:
mg R r 1 cos Jc 2  2 mvc2
2 mvc2  2 const.
2 const.
Здесь J |
c |
2mr2 5, v r. |
При |
|
малых |
колебаниях 1 cos 2 2. |
|||||||
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
С учетом (1) в итоге получаем: g 2 |
7 |
R |
d 2 |
const. Дифференцируя |
|||||||||
5 |
r |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
это уравнение по времени и сокращая на dφ dt , |
приходим к уравнению |
||||||||||||
гармонических колебаний: |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
d 2 |
|
5 |
|
g |
0. |
|
||
|
|
|
|
|
dt2 |
7 |
R r |
|
|||||
|
|
|
|
|
|
|
|
|
|||||
Следовательно, |
5 |
|
g |
|
|
|
|
|
|
|
|
||
7 R r |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||
43. Для составления уравнения движения достаточно использовать закон сохранения энергии. Пусть m – масса половинки арбуза, R – ее радиус.
39

|
O |
|
|
|
|
О |
|
|
|
|
|
φ |
Еп = |
0 |
δ |
|
|
|
|
СC |
φ |
|
|
|
|
Р |
|
|
|
|
P |
|
|
|
Потенциальная энергия фигуры равна
Eп mg cos ,
где δ = ОС – расстояние от центра масс С до линии сечения, по условию задачи равное R 5R 8 3R
8 3R 8.
8.
Для нахождения кинетической энергии удобно воспользоваться наличи-
ем мгновенной оси вращения Р. Тогда
Eк 12 JP 2 12 JP 2.
Определим JP, используя теорему Гюйгенса–Штейнера:
JP JC m PC 2 .
Момент инерции относительно центра масс JС удобно связать с момен-
том инерции относительно середины сечения JО, который нетрудно вычис-
лить:
JO 52 mR2, JO JC m 2 JC JO m 2.
Подстановка этого выражения и формулы
PC 2 2 sin2 R cos 2
ввыражение для JP приводит к следующему результату:
|
|
JP |
7 mR2 |
2mR cos . |
|
||||||||||
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, закон сохранения энергии примет вид |
|
||||||||||||||
|
7 |
mR2 2mR cos |
2 |
|
|
(1) |
|||||||||
|
5 |
|
2 |
mg cos mg . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
При малых |
колебаниях |
(угол |
φ мал) можно положить |
cos 1, |
|||||||||||
1 cos 2 2. Тогда (1) сведется к выражению |
|
||||||||||||||
|
|
13 |
R |
2 |
|
2 |
g |
2 |
0. |
(2) |
|||||
|
|
20 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Продифференцировав (2) по времени, получим уравнение гармониче- |
|||||||||||||||
ских колебаний: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 g |
0 . |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
26 R |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
40
