Sb95667

generation in GaSe crystal. Here are interacting the light wave with the wavelength λ3 = 1.06 μm and the wave with the tuned wavelength λ2 = 1.1 – 1.4 μm. The upper curve corresponds to the crystal length of 4 mm, and the lower one – 1.7 mm.

The reduce of energy of the generated pulses with the growth of the wavelength is caused first of all by the reduce of single quantum energy (ħω ~1/λ).

Wave presentation of such an effect makes it possible to take into account the influence of group velocity of waves, of dispersive washing out of the pulse etc. onto the efficiency of energy transfer from one wave to another. These effects are very important in the case of parametric generation of pulses with picoseconds and femtosecond duration.

of the pulse waveform. In most cases for different frequencies the group velocities differ even in the case of phase speeds equality. This effect reduces the efficiency of energy transfer from one wave to another (see Fig.2.4). Here are shown the

waveforms for three wavelengths. The narrow contours correspond to λ1 = 1.08 μm and λ2 = 1.46 μm, which are moving with practically one and the same velocities, while the wide contour corresponds to

λ3 = 0.62 μm, i.e. to the pumping pulse. Maximal intensity of each pulse is normalized to 1, because at different stages the intensity of pulses are strongly varying. In the first curve, shown in the Fig.2.4a, the first and second pulses have just arisen and coincide with the third pulse center. In the next curve, Fig.2.4b, they have shifted forward, and in the Fig.2.4c they have reached the forward front of the third pulse. To this moment the large part of the third pulse energy was already transferred to the first and second pulses.

На графике, показанном на рис. 2.4, а, первый и второй импульсы

21

Increase of pulse duration due to difference in phase speed of waves with different frequency, which comprise the pulse, is known as the dispersive washing out of the pulse. This effect is usually important for the pulses with duration of less than 1 ps. It leads to reduce of the light pulse intensity and thus of interaction efficiency. Both effects depend upon the dispersive properties of the crystal, where takes place the interaction. One has to shorten the crystal length so as to reduce their influence. However, the reduce of length results also in reduce of time of energy transfer from one wave to another. Hence the choice of the optimal crystal length is one more important task during design of nonlinear generator.

It is impossible to discuss all features of the three-wave interactions within one short tutorial book. In particular, we do not discuss here the role of the spatial effects – of the light beam profile, of the beam di sposition in the anisotropic crystal, beam self-focusing etc. We also do not discuss the influence of the linear and nonlinear absorption onto these effects. However, even this brief enumeration gives an understanding of complexity of the problem of nonlinear interaction of light waves in the crystal. Nevertheless, today second and higher harmonics generators, generators of summary and difference frequency and optical parametric oscillators are rather usual devices in laboratory and industrial laser devices.

Just in several years after first laser starting up in 1960 the first prototypes of all these devices were created, providing the basis for the further engineering progress. The very large role was played by Soviet and Russian scientists – in particular, by such prominent scientists as Prof. S.A.Akhmanov and Academician R.V.Khokhlov, who were one of founders of nonlinear optics.

One of important fields of science is the so called laser spectroscopy. Many of its experiments require the use of laser radiation with the frequency, which is smoothly tuned within the wide range. Many gases with the multi-atom molecules have the wide absorption spectra in the IR range. These spectra are investigated with the use of OPO radiation. Similar methods are used for investigation of complicated semiconductor structures. The most important advantage of this method is possibility of precise tuning of probe wavelength to the absorption band. Today are also coming to existence the new nonlinear generators on the base of three-wave interaction, which are especially important in the case of very short (femtosecond) pulses investigation and use. This field of science promises yet a lot of new discoveries and inventions.

22

3. STIMULATED SCATTERING OF LIGHT

3.1. Spontaneous and stimulated scattering of light

There exist several types of light scattering (see Fig.3.1):

1. Light scattering by separate atoms, molecules and, in general, by the particles whose size is much less than the radiation wavelength. It is known as the Rayleigh scattering. In this case the light intensity, scattered towards the direction, whose angle with the primary beam propagation direction is θ, obeys the law:

I p = λC4 (1 + cos2 θ),

Here λ is the light wavelength and С is a constant. This formula, in particular, explains why our sky is blue. It is so because the blue light is scattered in approximately 6 times stronger than the red one, whose wavelength is much larger. In the evening, when the light path through the atmosphere is especially long, the blue component is completely scattered and we can see the red Sun. In the case of Rayleigh scattering the electric field of the wave excites the oscillations of the electrons of atoms, and the oscillating electrons become the source of secondary scattered waves. In the case when the light frequency coincides with the resonant frequency of some atomic or molecular transition, the scattered intensity is growing due to the so called resonant fluorescence.

Fig. 3.1. Types of light scattering

23

2.The scattering of light by the particles whose size is comparable with the radiation wavelength is known as the Mie scattering. It is realized in suspensions and colloids, and strongly depends upon specific medium properties. Mie scattering is an important source of information about the properties of such media.

3.Molecular or spontaneous light scattering, which consists of several components, known as the Raman scattering, Brillouin scattering and Rayleigh wing scattering. The first of them, which is in Russian called also “combinatory” scattering, was discovered in 1928 simultaneously by Landsberg and Mandelstam in crystal, and by Raman and Krishnan in liquids. Raman scattering reveals itself by the

presence in the scattered radiation of the components with the frequencies ν + ΩR

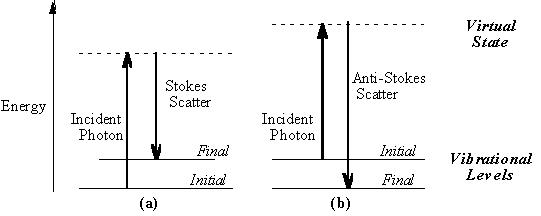
и ν − ΩR, where ν is the primary frequency of scattered radiation. The Raman scattering is the so-called non-elastic scattering, when light scattering is accompanied by its energy transfer to (or from) the matter. It means that scattering of light is accompanied by the atom or molecule transition from one quantum level to another. If the light wave is losing some part of its energy (hΩк) during such a transition, the scattered component at (ν − ΩR) = νS is known as the Stokes component. The atom or molecule in this case gets the energy and thus arises to higher energy level. In other case, known as the ant0Stokes scattering, the atom or molecule is transferred to the lower energy level, and the component at (ν + ΩR) = νAS is known as the anti-Stokes component.

Fig.3.2. Raman scattering of light

The essence of this effect is illustrated by the Fig.3.2. In the case of Stokes scattering (Fig.3.2a) the molecule in the initial fundamental state absorbs the quantum of the incident light hν and is transferred to some imaginary (virtual) state, and then is immediately transferred to the final state with emission of the quantum with the energy hνS = h(ν − ΩR). In the anti-Stokes case (Fig.3.2b) the molecule starts

24

from some excited initial level and finishes at the lower final one with emission of quantum with the energy hνAS = h(ν + ΩR). In both cases the difference of energy between initial and final states is equal to hΩR. Under the normal conditions the number of molecules in the fundamental lower state is larger that in the excited upper one (in ehΩR kT times), and hence the number of quanta with energy hνS will be in ehΩR kT times more than that with hνAS. Since the process includes absorption and emission of two photons, and each photon can have the spin value of ±1, the spin of the molecule after Raman scattering can either be preserved or to change in ±2; this is an obvious difference with the case of usual absorption or emission of single photon, when the molecule spin changes in ±1. Most usually the molecules or atoms have several pairs of levels, meeting this spin preservation requirement, and thus the Raman scattering spectrum reveals several pairs of Stokes and anti-Stokes lines, characterized by different value of hΩR.

Most usually the Raman scattering is observed with the use of molecular (vibrational and rotational) transitions, whose frequency shifts usually correspond to some 400…4000 cm -1 and are determined first of all by the oscillating molecular or atomic group. It is important that these frequencies are practically independent upon the specific compound and thus the Raman scattering provides a very important information about the structure of complicated molecules.

Molecular (atomic) oscillations are not the only forms of oscillations in the scattering matter – there also exist the so called collective movement forms, and such collective oscillations can also reveal themselves in the light scattering. These are, in particular, the well known sonic, i.e. acoustical waves, which represent the waves of matter pressure. Fluctuations of matter density or temperature result in variation of pressure, which, in turn, reveals itself in variation of the refraction index, which can lead to optical scattering. This effect was discovered in 1918 and is now known as Brillouin or Mandelstam-Brillouin scattering. It can be observed on the ultrasonic and hypersonic waves in media (, and also on some other types of molecular waves like magnons (spin waves in ferromagnetic) or plasmons (waves of conductivity electrons). Like Raman scattering, the Brillouin scattering also reveals itself as the pair of symmetrical with respect to the primary wavelength spectral lines, which are also called Stokes and anti-Stokes ones.

Spectrum of the Rayleigh-wing scattering is similar to that of Rayleigh scattering, but it is much wider. It is caused by fluctuations of the molecular orienta-

25

tion, resulting in local variations of medium birefringence.

4. Stimulated scattering of light has the same nature as spontaneous, but occurs only when the intensity of incident radiation is sufficiently high. The3 stimulated scattering is a nonlinear-optical effect, during which the intensity of the scattered light can become comparable with that of incident, while in the case of spon-

taneous scattering the intensity of scattered light is usually equal to some 10–4 … 10–6 of the incident intensity. The origin of the stimulated scattering is, in fact, rather similar to that of the parametric oscillation, considered in the previous section. In this case, however, ω3 = 2πν, i.e. it is the incident light frequency, and one of the frequencies ω1 or ω2 corresponds to the energy transfer to or from the medium to scattered light; for instance, in the case of stimulated Raman scattering (SRS) it determines the energy difference between the initial and final levels (hΩR = hω1/2π or hΩR = hω2/2π). The second of these frequencies thus corresponds to the frequency of Stokes 2πνS or anti-Stokes 2πνAS component. The process of stimulated scattering can be treated as amplification of the scattered wave (and of the corresponding molecular or collective oscillation of the medium) in the field of pumping, i.e. incident wave. The gain of such amplification depends upon

tion αP:

α = C I P − α P ,

Here IP is the “pumping” (i.e. incident) wave intensity, a nd C is some coefficient. Obviously, the stimulated scattering reveals itself only when IP > αP2/С2, i.e. when the incident light intensity is sufficiently high.

Important feature of stimulated scattering – to the contrary with its spontaneous analogue – is the strict coherence of the sca ttered radiation. Similarly to optical parametric oscillators, discussed in the previous section, SRS, SBS (stimulated Brillouin scattering) and other types of stimulated scattering can serve as la- ser-like converters of pumping radiation energy to that of the scattered one. Such generators, in particular, the so called SRS lasers (of course, these are not real lasers) are widely used for practical purposes.

Further we shall discuss in more details SRS and SBS as two most important for practical purposes types of stimulated scattering

26

3.2. Stimulated Raman scattering

The processes of stimulated scattering, and SRS in particular, are to a very large extent similar to the well known stimulated emission, which is the fundamental process in laser generation. In the case of stimulated emission the excited atom or molecule interacts with the resonant quantum, producing two identical quanta, while the atom is losing the correspondent amount of energy; hence, this process involves one quantum system and two quanta. In the case of stimulated scattering, the process involves one quantum system and three quanta. If this quantum system is reached simultaneously by two quanta, whose energy corresponds to the value of Stokes shift hΩR , there exists the probability that one of these quanta will disappear, producing the energy transfer of the quantum system and emission of the scattered quantum, which is identical to the second quantum, participating in this non-elastic scattering process. If the quantum system absorbs energy, which is more probable, we observe the Stokes SRS, in the opposite case – the anti-Stokes one.

SRS radiation usually contains series of Stokes ((wl – wυ), (wl – 2 wυ ) etc.) and anti-Stokes ((wl + wυ), (wl + 2wυ) etc.) components. The Stokes photon emission increases the vibrational level (u = 1) population, opening thus the possibility to emit the anti-Stokes quantum. Stokes (wS) and anti-Stokes (wAS) components can also be scattered, producing thus the components at wS – wυ = wl – 2 wυ and

wAS + wυ = wl + 2wυ.

Let us calculate the conditions of emission at the first Stokes frequency wS = wl – wυ, which is first to be amplified, because the emission of other SRS components requires either the presence of excited molecules or of the already existing first Stokes component. Let the medium consist of N independent oscillators, each of which is characterized by its position along the axis z (we shall consider the single dimension case when ¶/¶x = ¶/¶y = 0) and by its normal oscillatory coordinate

Here Г is the attenuation constant, meeting the requirement that the observed width of spontaneous Raman scattering line is equal to ν = Γ2π ; wυ is the resonant frequency of molecular vibrations in the absence of attenuation; m is the mass; and

F(z, t) is the excitation force.

One can evaluate the exciting force from consideration of the electromagnetic energy in the molecular medium. The energy, stored in the electromagnetic field E = 1/2eE2, taking into account the equality

The force, which is acting onto the unit volume of the polarized medium, is equal to ¶e/¶X. Division by N gives us the force, which is applied to one oscillator:

Here <E(z, t)> means the averaging per several oscillations, because the molecule cannot react onto these oscillations. One can see from (3.4) that if the dif-

28

ferential polarazability (∂α/∂X)0 is not equal to zero, the molecules can be excited by the electric field.

Now we are to reveal the action of molecular oscillations onto the electromagnetic field. According to (3.2) the molecular oscillations with the frequency ωυ lead to modulation of dielectric permittivity with the same frequency. So the phase modulation of the field takes place – one can now o bserve the components, shifted in ωυ. In other words, there takes place the energy exchange between the electromagnetic fields, whose frequencies are separated in the value of ωυ.

The total field is the sum of the laser (ω2) and Stokes (ω1) fields:

E ( z, t ) = 12 (E1 ( z) exp iϖ 1t + E2 ( z) exp iϖ 2t )+ c.c. ;

E(z, t) 2 = 14 E2 (z)E1* (z) exp i(ϖ 2 −ϖ1 )t + c.c.

Let us combine (3.6), (3.4) and further (3.1). We obtain:

So, with the use of equations (3.5), (3.9) and (3.10) we can get the following relationship for the nonlinear polarization, i.e. for the second term of polarization which is proportional to the field E:

Let us carry out the multiplication in (3.11), taking into account that

29

and thus we obtain the polarization components which oscillate with the frequencies ω14, ω24, 2ω1 − ω2 and 2ω2 − ω1. Let us first consider the first of them:

The coefficient of proportionality between the field and polarization is susceptibility. Similar to linear susceptibility, the nonlinear combinatory (Raman) susceptibility reveals the Lorentz line shape. The Stokes scattering line is described by the equation:

The anti-Stokes radiation at the frequency ω3 = ω2 + ωυ яresults from Raman scattering of light by the molecules, which are in the excited vibrational state υ = 1. The classical approach to this problem is based on search for polarization at the frequency ω3, induced by electric field:

Similarly to (3.11) let find in the relationship for polarization the term, which corresponds to excitation of molecular oscillations by the force, which is proportional to E3E2* . Modifying the indexes at frequencies and at E, we can get from (3.13)

Note that the imaginary terms of (3.13) and (3.15) have opposite signs. It

means that in the case if the anti-Stokes wave propagates through the Raman me-

30