
LS-Sb90324
.pdfгде V> и V= |
|
FПJ<>K = V> <>'FD ; FПH<=I = V= <='FD, |
|||
– |
|
величины, зависящие от геометрической формы |
|||
|
безразмерные |
2N |
2N |
||
сечения. |
|
|
|
|
|
Как |
правило, эти слагаемые значительно |
меньше остальных, и ими |
|||
можно пренебречь. Таким образом, потенциальная энергия деформации равна половине произведения сил или пары сил на перемещение по ее направлению в том сечении, где внутренняя сила приложена.
Сосредоточенную силу и сосредоточенный момент, вызывающие соответствующие перемещения, называют обобщенными силой и моментом,
а перемещение, вызванное этой силой, – |
обобщенным перемещением. |
|||||||||||||||||||
Потенциальную энергию всего стержня найдем, проинтегрировав |
||||||||||||||||||||
выражение для FП: |
2>'FD + W 2='FD |
+ W )'FD |
+ W V><>'FD + W V=<='FD. |
|||||||||||||||||
П = W |
2+'FD |
+ W |
||||||||||||||||||
X |
2N?O |
|
X |
2 ?> |
X |
|
2 ?= |
|
X |
2 |
|
X |
|
2N |
|
X |
2N |
|||
Теперь рассмотрим стержень длиной |
, жестко защемленный одним |
|||||||||||||||||||
концом. Известны геометрические характеристики стержня , |
?>, ?O, модуль |
|||||||||||||||||||
нормальной упругости материала |
, модуль упругости при сдвиге |
. |
||||||||||||||||||
К |
свободному |
торцу |
|
стержня |
|
последовательно |
|
Nприложим |
||||||||||||
растягивающую силу |
, скручивающий момент |
|
и изгибающий момент |
|||||||||||||||||
Накопленная в |
стержне |
потенциальная энергия2к |
упругой деформации |
|||||||||||||||||
численно2и. |
|
|
|
|
|
)' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равна работе каждой из этих внешних сил: |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
^ |
|
|
|
|
|
|
|
к |
и |
= 0; |
|
|
|
||
|
|
|
|
|
|
2 при ≠ 0, 2 = 2 |
|
|
|
|
||||||||||
|
|
|
П = ] |
2к'FD |
при 2к ≠ 0, = 2и = 0; |
|
|
|
||||||||||||
|
|
|
2N?O |
|
|
|
||||||||||||||
|
|
|
|
|
|
2и'FD |
при 2и ≠ 0, 2к = = 0. |
|
|
|
||||||||||
|
|
|
|
|
|
2 ?> |
|
|
|
|||||||||||
Рассмотрим |
производные |
|
от |
энергии |
упругой |
деформации по |
||||||||||||||
|
[ |
LП |
|
2к |
|
|
LП |
|
2и |
|||||||||||
|
LП |
|
|
|
|
|
|
|
|
|
||||||||||
соответствующей обобщающей силе: |
|
= ∆Θ; L2к |
= ?> = ∆φ. |
|
||||||||||||||||
|
L |
|
= |
= ∆ ; L2к |
= N?O |
|
||||||||||||||
Производная от энергии упругой деформации по обобщенной силе равна перемещению, соответствующему этой силе по линии действия силы.
21
Эта закономерность в общем виде была установлена Кастильяно и сформулирована им в качестве теоремы.
Рассмотрим общий случай нагружения упругого тела. Пусть оно закреплено так, что при нагружении невозможно его смещение как жесткого
целого. Тело испытывает деформацию под действием |
обобщенных сил |
|||||
, ', . . . , . Энергию упругой деформации выразим функцией этой группы |
||||||
сил: П = ПH , ', . . . , I. Если одной из внешних сил, например |
, придать |
|||||
|
|
П = П + LП F . |
|
|
|
|
небольшое приращение F , то энергия упругой деформации возрастет: |
||||||
|
|
сначала была приложена бесконечно |
||||
Возьмем другой случай. Допустим,L |
|
|
|
|
||
малая сила |
, вызывающая бесконечно малое перемещение. Работой силы |
|||||
можно пренебречьF |
как бесконечно малой величиной второго порядка по |
|||||
сравнениюF |
с работой приложенных затем сил |
. Потенциальная |
||||
энергия упругой деформации, вызванной этими силами, ', . .,. ,по-прежнему равна |
||||||
П. В точке приложения силы произойдет конечное перемещение |
δ , при |
|||||
котором малая сила F , приложенная вначале, совершит работу |
δ F . |
|||||
Тогда накопленная потенциальная энергия |
|
. |
|
|
||
Потенциальная энергия деформации неП зависит= П + δ отF порядка |
, в котором |
|||||
|
|
LП |
следовательно, |
|
|
|
прикладываются силы, поэтому П = П и, |
|
|
|
|||
откуда |
|
П + L F = П + δ F , |
|
|
|
|
|
|
LП |
|
|
|
|
|
|
δ = L . |
|
|
|
|
Сформулируем теорему Кастильяно:
Частная производная от потенциальной энергии упругой деформации по обобщенной силе равна обобщенному перемещению точки приложения силы по направлению силы.
Под перемещением в заданном направлении понимают проекцию полного перемещения на заданное направление. Перемещение точки приложения силы по направлению силы – это проекция на направление силы полного перемещения этой точки.
22

4.3.1. Расчет перемещений в точке узла конструкции при ускорении de,
действующем вдоль оси конструкции
Рассмотрим стержень (рис. 4.5), который подвергается деформации
растяжения-сжатия. Перемещение определяется по формуле |
||||
|
|
L) |
|
|
|
δр = 8 |
) L |
FD. |
|
|
|
|||
|
|
H Iпр |
|
|
Для |
определения перемещения |
крайней |
||
правой точки стержня необходимо записать |
||||
выражения для нормальной силы |
на |
каждом |
||
грузовом |
участке, продифференцировать) |
|
их по |
|
силе и найти значения перемещений на каждом
участке.
Рис. 4.5
Значение H Iпр рассчитывается для каждого грузового участка исходя
из данных о реальной конструкции. Например, рассмотрим третий грузовой участок. На этом участке схема состоит из двух элементов (см. рис. 4.1, а),
H I = + .
расположенных параллельно. Следовательно, приведенное значение
A A A A A пр ' '
Аналогично находятся значения и для остальных участков.
4.3.2. Расчет перемещений в точке узла конструкции при ускорении de,
действующем по нормали к оси конструкции
Рассмотрим стержень (рис. 4.6), который подвергается деформации плоскопоперечного изгиба. При этом виде деформации возникает линейное
перемещение по обобщенной силе |
|
|
L2> |
|
|
|
|
|
|
||
δр = 8 |
2> L |
FD |
|||
|
|
|
|||
|
J ?>Kпр |
|
|||
и угловое перемещение (угол поворота) |
L2> |
|
|||
|
|
|
|
|
|
θ = 8 |
2> |
|
L2 |
FD. |
|
|
|
|
|
||
|
|
J ?>Kпр |
|
||
|
|
|
|
23 |
|

Для определения перемещения крайней правой точки стержня |
|||||||||||||
необходимо записать выражения для изгибающего момента 2> |
на каждом |
||||||||||||
грузовом участке, |
продифференцировать |
их по силе |
|
для |
линейного |
||||||||
|
перемещения и по |
для угла поворота, а затем найти |
|||||||||||
|
значения перемещений2 |
на каждом участке. |
|
||||||||||
|
|
Значение J ?>Kпр |
рассчитывается для каждого |
||||||||||
|
грузового участка исходя из данных о реальной |
||||||||||||
|
конструкции. Для третьего грузового участка, |
||||||||||||
|
состоящего |
из двух |
элементов (см. рис. 4.2, а), |
||||||||||
Рис. 4.6 |
расположенных параллельно: |
|
πi |
|
|
||||||||
|
A |
A |
A |
|
A |
A |
|
πg |
|
|
|
||
J ?>Kпр |
= |
?> |
+ ' |
?>', ; ?> = |
|
− |
|
|
, |
|
|||
|
|
|
|
||||||||||
причем осевой момент инерции |
|
рассчитывается отдельно для каждого |
|||||||||||
?> |
|
|
|
4 |
|
|
4 |
|
|
||||
элемента внутри этого участка. |
|
|
|
|
|
|
|
|
|
||||
Аналогично находятся значения J ?>Kпр для остальных участков.
4.4. Определение низшей частоты собственных колебаний корпуса прибора
При эксплуатации приборы подвергаются динамическим воздействиям: ударам, за малый промежуток времени изменяющим скорости точек тела на конечное значение, и вибрациям, механическим колебаниям. Под колебаниями понимают движения или процессы, обладающие той или иной повторяемостью во времени.
Вибропрочность электронных приборов и устройств приобрела особое значение, как только эти приборы стали частью автоматизированных систем, применяемых в промышленности и на транспорте. Вредные, не являющиеся необходимым условием выполнения конструкцией своих функций, вибрации возникают из-за несовершенства конструкции, дефектов в ее элементах или особых условий действия и эксплуатации, например из-за несбалансированности деталей. Вибрации приводят к разрушению деталей и ослаблению зажимов и винтовых соединений. Если упругую систему вывести из равновесия, то силы упругости системы в новом положении уже не будут уравновешиваться и возникнут колебания.
24
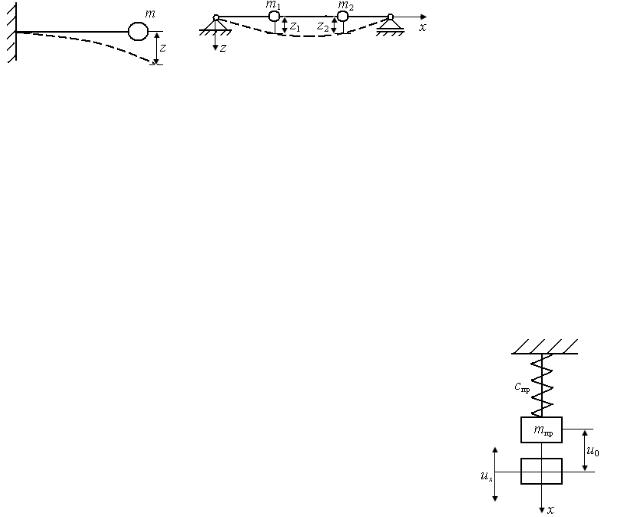
При построении расчетной схемы наиболее легкие элементы конструкции можно считать безмассовыми, безынерционными деформируемыми связями.
Конструкция может быть описана системой с одной (рис. 4.7, а), двумя (рис. 4.7, б) или большим числом степеней свободы. Под числом степеней свободы понимают число независимых параметров, однозначно определяющих положение системы в данный момент времени. Любая конструкция содержит бесконечное число материальных точек и, следовательно, имеет бесконечное число степеней свободы. Стержень с распределенной массой представляет собой систему с бесконечным числом степеней свободы (рис. 4.7, в).
|
б |
а |
в |
|
Рис. 4.7 |
Собственные частоты колебаний являются обобщенными приведенными параметрами динамической расчетной схемы. Определение собственных частот колебаний – важная задача. Изделия при эксплуатации испытывают воздействие различных вынуждающих сил, переменных во времени, не зависящих от состояния системы и поддерживающих ее колебания. При совпадении или относительной близости собственных частот колебаний и частот вынуждающих сил появляются резонансные эффекты.
Рассмотрим линейные динамические расчетные
законом динамики:
схемы с одной степенью свободы. |
|
|
|
Допустим, система, представленная на рис. 4.8, |
|
||
выведена из состояния статического равновесия. |
|
||
Инерционный элемент с приведенной массой |
пр |
|
|
перемещен на . |
|
|
|
Внешние R& возбуждающие |
силы отсутствуют. |
|
|
Составим уравнение движения, |
пользуясь вторым |
Рис. 4.8 |
|
|
Rj = . |
|
|
|
|
||
пр +
Равнодействующая внешних сил равна восстанавливающей силе: 25

Введя обозначение |
|
= −kпрR+. |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
ω |
' |
= |
kпр |
|
|
|
|
|
|
|
|
|
|
|
|||
получим |
|
|
|
|
|
пр, |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Rj + ω |
R |
|
= 0. |
|
|
|
|
|
|
|
|
|
||||||
Получим |
|
|
|
+ |
|
|
|
' |
+ |
|
|
|
|
|
|
|
|
|
|
|
R+ = m |
9n. |
Составим характеристическое уравнение по методу Эйлера |
|
|||||||||||||||||||||
|
|
V' + ω' = 0, |
V' = −ω' , |
V = ± ω. |
|
: pn удобно |
||||||||||||||||
Для дальнейшего анализа показательные функции |
m |
pn и |
m |
|||||||||||||||||||
Постоянные |
|
R |
= q sin ωu + v cos ωu. |
|
|
|
|
|
||||||||||||||
представить тригонометрическими: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интегрирования определяют из начальных условий. При |
||||||||||||||||||||
перемещение |
|
скорость |
+ |
|
|
, следовательно, |
|
|
& |
|
||||||||||||
Выражениеu = 0 |
свободногоR+ = R&, |
движенияRy =возбужденной0 |
системыv = R , qносит= 0. |
|||||||||||||||||||
гармонический характер: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Введенную ранее величинуR+ =(числоR& cos колебанийωu. |
за время |
|
) называют |
|||||||||||||||||||
угловой собственной частотой колебанийω |
, рад·с – 1 |
: |
|
|
|
2π |
|
|
||||||||||||||
|
|
|
|
ω = zk |
|
|
пр |
. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
пр⁄ |
|
|
|
|
|
|
|
|
|
|
|
|
||
Кроме угловой определяют линейную собственную частоту колебаний {, Гц: |
||||||||||||||||||||||
|
|
|
|
{ = |
ω |
= |
1 |
|
| |
kпр |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2π |
2π |
|
пр |
. |
|
|
|
|
|
|
|
|
||||||
При расчете низшей частоты собственных колебаний корпуса изолятора приведем схему корпуса с распределенной массой (рис. 4.9, а) к схеме с
одной степенью свободы (рис. 4.9, б). Она состоит из безынерционного |
|||
участка длиной l с приведенной изгибной жесткостью |
J ?>Kпр и |
||
сосредоточенной приведенной массы пр. |
|
, |
|
Массу последнего участка представим как сосредоточенную массу |
|||
приложенную в центре масс последнего участка. Массы всех остальныхс |
|||
участков – распределенные массы р |
= ρ ~ , р' = ρ'~', . . . , р = ρ ~ . |
|
|
Тогда приведенная масса |
+ 0,23 р, |
|
|
пр = с |
|
|
|
|
26 |
|
|

где р = р + р' + + р . |
|
Коэффициент жесткости для |
участка с жесткой заделкой с одной |
стороны |
3J ?>K |
k = |
A . |
а |
б |
|
|
|
Рис. 4.9 |
Для схемы на рис. 4.9, а все участки являются последовательными,
следовательно, приведенная жесткость |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
|
1 ; |
|
A |
= |
|
A |
|
+ |
|
|
|
'A |
|
+ + |
A |
|
. |
|||||
= 8 |
|
|
K |
|
|
|
K' |
K |
|||||||||||||||
kпр |
|
k |
3J ? Kпр |
|
3J ? |
|
|
3J ? |
|
|
|
|
3J ? |
|
|||||||||
|
|
> |
|
|
> |
|
|
|
|
|
|
> |
|
|
|
|
|
> |
|
|
|||
|
|
|
|
|
|
|
3J ?>Kпр |
|
б: |
|
|
|
|
|
|
|
|
||||||
Коэффициент жесткости для схемы на рис. 4.9, |
|
|
|
|
|
|
|
|
|||||||||||||||
Тогда |
|
|
|
|
kпр = |
|
|
A |
. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
kпр |
|
1 |
| |
|
|
|
|
3J ?>Kпр |
|
|
|
|
|
|
|||||
|
|
{ = 2π |
| пр |
= 2π |
|
J |
соср |
|
|
|
р |
K |
A |
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ 0,23 |
|
|
|
|
|
||||||
Список литературы
1.Бегун П. И., Кормилицын О. П. Прикладная механика. – СПб.: Политехника, 1995.
2.Феодосьев В. И. Сопротивление материалов. – М.: Изд-во МГТУ им. Н. Э. Баумана, 2007.
27

ПРИЛОЖЕНИЕ
Рис. П. 1
28

Рис. П. 2
29
Рис. П. 3
30
