sb000001

образом, при совместной диффузии функцией поверхностной или максимальной концентрации носителей в эмиттере оказывается не только коэффициент диффузии эмиттерной примеси

но и коэффициент диффузии базовой примеси

При численном моделировании совместной диффузии необходимо рассчитывать перераспределение сразу двух примесей, т.е. решать совместно два уравнения диффузии типа (4.13). В общем случае максимальная концентрация носителей n1max

является функцией времени и поэтому на каждом новом шаге по времени необходимо переопределять параметры L1 и L2. При задании числа шагов по времени в качестве величины М для сходимости решений по обеим примесям необходимо брать максимальное из двух минимальных значений М1 и М2, определяемых выражениями вида

(4.16).

Блок–схема программы совместной диффузии легирующих примесей приведена в прил.13.

4.12. Расчет положения p–n–перехода и слоевого сопротивления

После проведения технологического процесса легирования осуществляется контроль параметров полупроводниковых слоев – глубины залегания p–n–перехода Xj и слоевого (поверхностного) сопротивления Rs. Имея в качестве результата численного моделирования профили распределения легирующих примесей по глубине, можно рассчитать модельные значения этих параметров.

Положение p–n–перехода определяется из условия равенства концентраций донорной Cd и акцепторной Ca примесей

Cd X j Ca X j .

Для определения Xj по значениям сеточных функций Cd I и Ca I производится последовательный перебор значений разности Cd I Ca I до тех пор, пока она при

некотором значении I = I* не поменяет знак. Положение p–n–перехода находится с помощью линейной интерполяции между точками I* и I* – 1.

Поверхностное сопротивление легированного слоя (слоевое сопротивление) Rs опре– деляется следующим выражением:

21

где q – заряд электрона (q = 1,6·10–19 Кл), М – подвижность носителей заряда. В качестве Cd и Ca в (4.27) необходимо брать концентрации электрически активных донорной и акцепторной примесей (выражения (4.5) – (4.8)). Зависимость подвижности от координаты M(x) определяется зависимостью подвижности от концентрации основных носителей заряда – электронов n или дырок p, которые в общем случае зависят от глубины. Аппроксимационная формула зависимости подвижности от концентрации носителей заряда n или p имеет вид [20]

M x M min M max M mina .

1 nCr

Значения параметров Mmin, Mmax, Cr и a для донорных и акцепторных примесей в кремнии приведены в прил.8.

Список литературы

1.Положение об организации курсового проектирования в институте / Под ред. В.И.Тимохина; ЛЭТИ. Л., 1979.

2.Методические указания по выполнению учебных документов/Под ред. В.И.Тимохина; ЛЭТИ. Л., 1980.

3.Тилл У., Лаксон Дж. Интегральные схемы. М.: Мир, 1985. Гл.11,14. С.292–336, 414–

495.

4.Аваев Н.А., Наумов Ю.Е., Фролкин В.Т. Основы микроэлектроники. М.: Радио и связь, 1991. Гл.7,8. С.120–180.

5.Першенков В.С.,Севастьянов А.В. Интегральные БиМОП микросхемы // Зарубежная электронная техника. 1989. Вып.12. С.49–87.

6.Технология СБИС / Под ред. С.Зи. М.: Мир, 1986. Кн.2. Гл.10,11. С.112–270.

7.Ефимов И.Е., Козырь И.Я., Горбунов Ю.И. Микроэлектроника. М.: Высш. шк., 1986.

Гл.9. С.286–339.

8.Бубенников А.Н. Моделирование интегральных микротехнологий, приборов и схем.

М.: Высш. шк., 1989. Гл.2. С.27–74.

9.Таблицы параметров пространственного распределения ионно–имплантированных примесей / А.Н.Буренков, Ф.Ф.Комаров, М.А.Кумахов, М.М.Темкин; БГУ. Минск, 1980.

10.Александров О.В., Ашкинадзе Н.В., Тумаров Р.З. Комплексообразование при диффузии фосфора в кремний // ФТТ. 1984. Т.26. Вып.2. С.632–634.

22

11.Tsukamoto K., Akasaka Y., Kijima K. Thermal diffusion of ion–implanted As in Si // Japan. J. Appl. Phys. 1980. Vol.19. N 1. P.87–95.

12.Бубенников А.Н., Садовников А.Д. Физико–технологическое проектирование биполярных элементов кремниевых БИС. М.: Радио и связь, 1991. Гл.2. С.47–108.

13.Дьяконов В.П. Справочник по алгоритмам и программам на языке Бейсик для ПЭВМ. М.: Наука, 1987.

14.МОП СБИС. Моделирование элементов и технологических процессов/Под ред. П.Антонетти. М.: Радио и связь, 1988. Гл.7. С.195–222.

15.Колоссовский А.В. Перераспределение примесей в процессе термического окисления // Обзоры по электронной технике. Сер.2. 1971. Вып.6(288). С.3–51.

16.Паометс В.Т. Расчет профиля распределения бора при многоэтапной диффузии в окислительных средах // Электронная техника. Сер.2. 1978. Вып.3(121). С.63–66.

17.Miller R.C., Smits F.M. 0Diffusion of Sb out of Ge and some properties of Sb–Ge system

//Phys.Rev. 1957. Vol.107, N 1. P.65–70.

18.Matsumoto S., Niimi T. Phosphorus diffusion into Si under the condition of controlled surface concentration//Japan. J. Appl. Phys. 1976. Vol.15, N 11. P.2077–2082.

19.Справочник по специальным функциям / Под ред. М.Абрамовица, И.Стигана. М.:

Наука. 1979.

20.Caughey D.V., Thomas R.E. Carrier mobilities in silicon empirically related to doping and field //Proc.IEEE. 1967. Vol.55, N 2. P.2192–2195.

21.Fair R.B., Tsai J.C.C. Theory and direct measurement of B segregation in SiO2 during dry, near dry and wet O2 oxidation // J.Electrochem. Soc. 1978. Vol.125, N 12. P.2051–2058.

22.Диффузионно–сегрегационное перераспределение донорных примесей в системе двуокись кремния – кремний / О.В.Александров, Н.Н. Афонин, А.П.Гурьянов, А.П.Коварcкий // Вопросы радиоэлектроники. Сер.ТПО. 1989. N 2. С.50–55.

23.Fair R.B., Tsai J.C.C. The diffusion of ion implanted As in Si // J. Electrochem. Soc. 1975. Vol.122, N 12. P.1689–1696.

24.Ho C.P., Plummer S.E., Dutton R.W. VLSI process modelling–SUPREM 3 //IEEE Trans. El. Dev. 1983. Vol.ED–30, N 11. P.1438–1453.

25.Ghoshtogore R.N. 0Low concentration diffusion in Si under sealed tube conditions // Sol. St. Electron. 1972. Vol.15, N 10. P.1113–1120.

26.Испарение и сегрегация галлия при нагреве легированного кремния в вакууме /А.В.Кожухов, Б.З.Кантер, С.И.Стенин и др. // Поверхность. 1989. N 30. С.160–161.

27.Испарение сурьмы из кремния в вакуум / А.В.Кожухов, Б.З.Кантер, Ю.Г.Сидоров, С.И.Стенин // Поверхность. 1990. N 9. С.30–36.

ПРИЛОЖЕНИЯ

23

1. Параметры распределения Пирсона для ионов B, P, As, Sb в мишени Si [9]

5. Коэффициенты сегрегации легирующих примесей в системе SiO2–Si(111)

24

6. Параметры температурной зависимости коэффициентов испарения и диффузии легирующих примесей в кремнии

7. Параметры парциальных коэффициентов диффузии основных легирующих примесей в кремнии [6,24]

8. Параметры концентрационной зависимости подвижности носителей заряда в кремнии [20]

25

9. Бейсик–программа решения уравнения диффузии при D=const

10 REM PROGRAM ALEX1

20 PRINT "Решение уравнения диффузии по явной схеме с D=const" 30 PRINT "н.у. C(x,0)=FNF(x), г.у. dC(0,t)/dx=0, C(H,t)=0"

40 PRINT "Введите коэффициент диффузии D, см520/с" 50 INPUT D

60 PRINT "Введите толщину слоя H, см и время диффузии T, с" 70 INPUT H,T

80 PRINT "Введите число шагов по глубине N"

90 INPUT N

100 PRINT"Введите число шагов по времени M (M>=";2·D·T·N·N/H/H;")"

110 INPUT M

120 DIM C(N,M)

130 DEF FNF(x)=C(x,0)

140 H1=H/N

150 T1=T/M

160 L=D*T1/H1/H1

170 REM Ввод начального распределения

180 FOR I=0 TO N

190 C(I,0)=FNF(I*H1)

200 NEXT I

210 REM Решение разностного уравнения

220 FOR J=0 TO M–1

230 FOR I=1 TO N–1

240 C(I,J+1)=L*C(I–1,J)+(1–2*L)*C(I,J)+L*C(I+1,J)

250 NEXT I

260 REM Учет граничных условий

270 C(0,J+1)=C(1,J+1)

280 C(N,J+1)=0

290 NEXT J

300 REM Печать таблицы

310 PRINT "X,см", "C,см–3"

320 FOR I=0 TO N

330 PRINT I*H1, C(I,M)

340 NEXT I

400 END

26

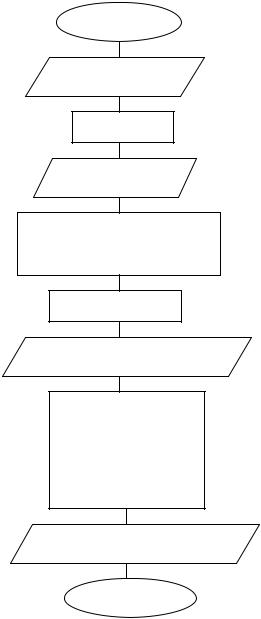
10. Блок–схема программы решения уравнения диффузии при D=const

Начало

Ввод D, H, T, N

Расчет Mmin

Ввод M>=Mmin

Описание массивa C(N,M) Определение функции нач.распред.FNF(x)

Расчет H1, T1, L

Ввод нач.распред.C(I,0)

FOR J=0 TO M–1 FOR I=1 TO N расчет C(I,J+1) NEXT I

учет гран.условий

NEXT J

Печать табл.I*H1,C(I,M)

Конец

27

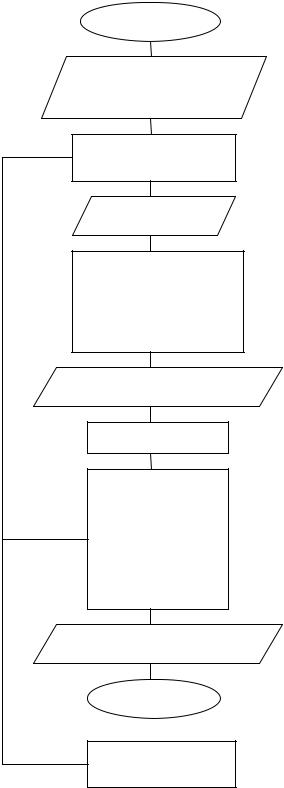
11. Блок–схема программы решения уравнения диффузии при D=D(C)

Начало

Ввод H, T, N

Ввод температуры Z

Расчет D ,D ,D ,Ni

Расчет Dmax,Mmin

Ввод M>=Mmin

Описание массивов

C(N,M), CN(N), D(N)

Определение функции нач.распред.FNF(x)

Расчет H1, T1, L

Ввод нач.распред.C(I,0)

Расчет нач. D(I)

FOR J=0 TO M–1 FOR I=1 TO N расчет C(I,J+1)

расчет D(I)

NEXT I

учет гран.условий

Печать табл.I*H1,C(I,M)

Конец

Подпрограмма расчета CN по C

28

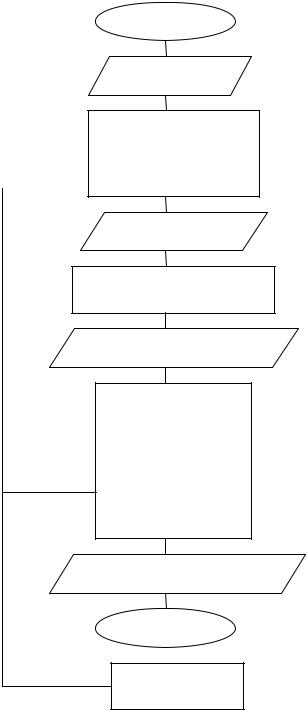
12. Блок–схема программы диффузионной разгонки с D=D(t)

Hачало

Ввод H,T,N,Z

Расчет D ,D ,D , Ni

Определение функции нач.распред. FNF(x) Расчет Dmax, Mmin

Ввод M>=Mmin

Описание массива C(N,M) Расчет H1,T1, нач.L

Ввод нач.распред.C(I,0)

FOR J=0 TO M–1 FOR I=1 TO N расчет C(I,J+1)

поиск Cmax

NEXT I

расчет D,L

учет гран.условий

NEXT J

Печать табл.I*H1, C(I,M)

Конец

Подпрограмма расчета CN по C

29

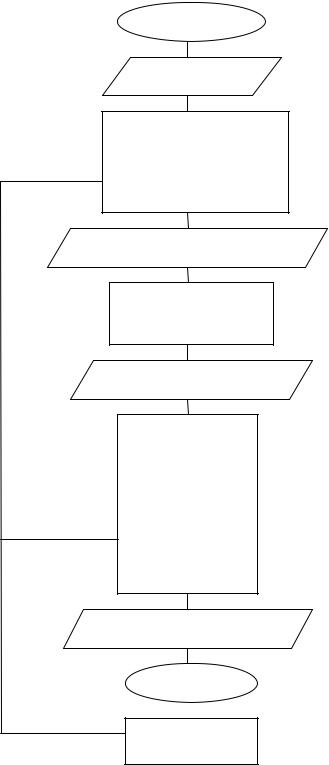
13. Блок–схема программы совместной диффузии с D2 = D(n1max)

Начало

Ввод H, T, N, Z

Расчет D1i, D2i, Ni Опред.нач. FNF1(x) Опред.нач. FNF2(x)

Расчет нач.C1max, D1, D2 Расчет M1min,M2max

Ввод M>=max(M1min,M2max)

Описание массивов

C1(N,M), C2(N,M) Расчет H1, T1, L1, L2

Ввод нач.C1(I,0),C2(I,0)

FOR J=O TO M–1 FOR I=1 TO N расчет C1(I,J+1) расчет C2(I,J+1)

поиск C1max

NEXT I

расчет Dmax, L1, L учет

гран.условий

Печать табл.I*H1, C1, C2

Конец

Подпрограмма расчета CN по C

30