5535

6.Подставим начальные условия из п. 1 в уравнение п. 5, найдем

II. Определим э.д.с. самоиндукции индуктивности.

Поскольку э.д.с. самоиндукции связана с током через индуктивность

коммутации эта э.д.с. равна напряжению на сопротивлении R2, а в дальнейшем уменьшается по экспоненциальному закону (рис. 3.11 б)

i(t) I0

−I0 e

Рис. 3.11 Переходные процессы в RL-цепи с коротким замыканием: а) ток через катушку; б) э.д.с. самоиндукции и напряжение на катушке.

Выводы.

∙При коротком замыкании в рассматриваемой цепи ток в ней изменяется по экспоненциальному закону, уменьшаясь от начального значения до нуля.

∙Скорость изменения тока определяется постоянной времени цепи, которая равна индуктивности катушки, деленной на активное сопротивление цепи.

∙Практически можно считать, что переходный процесс заканчивается при t ≈ (3…5) τ , когда первоначальное значение тока уменьшается по модулю на порядок.

∙Напряжение на индуктивности в начальный момент времени равно напряжению на активном сопротивлении: u L (0 + ) = I 0 R2 .

∙С энергетической точки зрения рассматриваемый переходный процесс характеризуется расходом энергии магнитного поля индуктивности на тепловые потери в резисторе. Следует отметить, что сопротивление резистора влияет не на количество выделенной теплоты W, а на начальное значение

3.2.8 Включение цепи с резистором и индуктивностью на постоянное напряжение

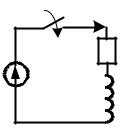
Дана электрическая схема RL-цепи, к которой подключено постоянное напряжение E=const. Рассчитать переходный ток через индуктивность и напряжение на индуктивности.

Рис. 3.12. Электрическая схема RL – цепи с постоянным напряжением E.

I. Определим переходной ток через индуктивность.

Воспользуемся порядком анализа переходных процессов (п.3.1).

1.Рассчитаем граничные условия и заполним таблицу граничных условий:

Рис. 3.13. Электрические схемы, поясняющие расчеты граничных условий

1)рассчитаем установившийся режим в цепи до коммутации (до замыкания ключа) в момент t = 0 (рис. 3.13 а) и определим из него независимое начальное условие — ток через индуктивность, непосредственно предшествующий коммутации i(0− ) = 0 ;

2)рассчитаем зависимые начальные условия в момент времени t = 0+

(рис.3.13 б) — напряжение на индуктивности uL (0+ ) при условии

выполнения законов коммутации, а именно, i(0+ ) = i(0− ) = 0 . Составим уравнение по 2-му закону Кирхгофа:

uL (0+ ) + i(0+ ) × R2 = E uL (0+ ) = E ;

3) рассчитаем установившийся режим в цепи после коммутации в

2. Составим дифференциальное уравнение для нахождения свободной составляющей (при Е = 0) в схеме после коммутации (рис. 3.13 б) по 2-муI

находить нет необходимости, поскольку для нахождения постоянной

6. Подставим начальные условия из п. 1 в уравнение п. 5, найдем

RR R

8.Расчеты значений переходного тока внесем в таблицу 3.5. и построим

график рис. 3.14 а:

i(t)

IУСТ

i(t)

-E

__

R

Рис. 3.13. Переходные процессы в RL-цепи с постоянным напряжением: а) ток через индуктивность; б) напряжение на индуктивности.

График переходного напряжения представлен на графике рис. 3.14 б.

Выводы.

∙При включении рассматриваемого контура под постоянное напряжение ток в нем нарастает от нуля до установившегося значения. Скорость нарастания

экспоненциально стремиться к установившемуся значению, а напряжение экспоненциально снижается до нуля.

3.2.9 Включение цепи с резистором и индуктивностью на синусоидальное напряжение

Дана электрическая схема RL-цепи, к которой подключено постоянное напряжение e(t) = E × cos( ωt + Y ) . Рассчитать переходный ток через

индуктивность.

Рис. 3.15 Электрическая схема RL – цепи с переменным напряжением e(t).

п.п. 5.-6. Используя независимые начальные условия при t = 0 i(0+ ) = i(0− ) = 0 ,

находим постоянную интегрирования: A = - Em × sin(Y - ϕ ).

Z

7. Переходный ток равен:

8. Рассчитаем значения переходного тока и построим график. Зависимости переходного тока от времени при различных значениях разностей ψ - φ показаны на рис. 3.16 а.

Рис. 3.16 Переходные процессы в RL-цепи с гармоническим напряжением

переменных, т.е. происходит алгебраизация интегро-дифференциальных уравнений послекоммутационной системы. При решении этих уравнений находятся изображения и далее путем обратного перехода возвращаются к оригиналам цепи.

Основным моментом при расчете операторным методом является только определение независимых начальных условий. Далее на основе ННУ происходит переход от оригинала к изображению, что существенно облегчает расчет переходных процессов в цепях высокого порядка по сравнению с классическим методом.

3.3.1 Прямое преобразование Лапласа

Переход от функции времени f(t) (оригинал) к некоторой комплексной функции F(p) осуществляется с помощью преобразования Лапласа.

Изображение F(p) заданной функции f(t) определяется в соответствии с

прямым преобразованием Лапласа:

( ) = W ‚ ∙ (€) [€. (3.26)

В сокращенной записи соответствие между изображением и оригиналом обозначается, как:

6. Изображение интеграла функции имеет следующий вид [7]:

(€) ( ).

В качестве примера в табл. 3.5 приведены изображения некоторых характерных функций, часто встречающихся при анализе нестационарных режимов.

Исходя из свойств производной функции и интеграла функции, можно установить соответствие между оригиналом и изображением для напряжения на индуктивности: