1284

40

модели делению моделируемой системы на функциональные блоки. Функциональные модели отображают как структуру, так и процессы функционирования объекта и чаще всего имеют форму систем уравнений.

По способам получения функциональные математические модели делят на теоретические и формальные. Теоретические модели получают на основе изучения физических закономерностей; структура уравнений и параметры моделей имеют определенное физическое толкование. Формальные модели получают на основе проявления свойств моделируемого объекта во внешней среде. Теоретический подход в большинстве случаев позволяет получать математические модели более универсальные, справедливые для широких диапазонов изменения внешних параметров. Формальные модели по сравнению с теоретическими более точны в окрестностях той точки пространства параметров, вблизи которой они определялись, но менее точны вдали от этой точки.

Пример формальной и теоретической функциональных моделей. Требу-

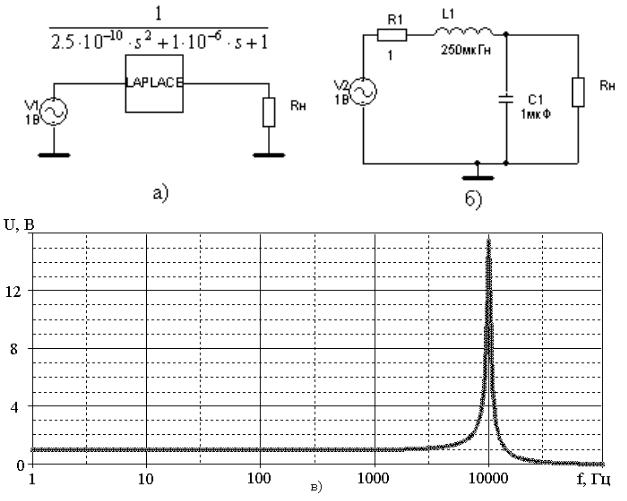
ется разработать функциональную модель звена второго порядка. Рассмотрим способы представления функциональных моделей с помощью программы схемотехнического моделирования PSpice A/D [8]. Если заранее известна передаточная функция звена, то можно применить стандартный для программы PSpice A/D функциональный блок LAPLACE (рисунок 2.24, а). Функциональный блок LAPLACE позволяет задавать в аналитическом виде и рассчитывать с помощью преобразования Лапласа передаточную функцию какоголибо звена. При этом определяются значения комплексного коэффициента передачи звена на каждой частоте (рисунок 2.24, в).

Если требуется более детальная проработка звена второго порядка, следует составить теоретическую функциональную модель (рисунок 2.24, б). В этом случае функциональная модель состоит из образов реальных электрорадиоэлементов, которые описываются соответствующими математическими выражениями. Реализуемая функция теоретической функциональной модели совпадает с реализуемой функцией формальной функциональной модели (рисунок 2.24, в).

Следует акцентировать внимание на следующих важных особенностях приведенных выше функциональных моделей:

1.Применение функциональных моделей избавляет исследователя от составления громоздких аналитических моделей.

2.Формальная функциональная модель (рисунок 2.24, а) используется только для проявления свойств исследуемого звена. Теоретическая функциональная модель (рисунок 2.24, б) дает физическое толкование наблюдаемого процесса, поскольку можно видеть как структуру звена, так и процесс его функционирования.

3.Представленные функциональные модели нельзя рассматривать в отрыве от их внутреннего содержания – комплекса математических выражений, заложенного в программе схемотехнического моделирования. В противном случае, внешнее проявление таких моделей можно было бы трактовать

41

как символические модели, а внутреннее проявление – как аналитические, что в принципе неверно.

а) – внешнее проявление формальной модели; б) – внешнее проявление теоретической модели; в) – реализуемая функция

Рисунок 2.24 – Функциональные модели в программе PSpice A/D

Математические модели классифицируются в соответствии с теми характеристиками моделируемого объекта, которые обусловливают применение того или иного математического аппарата при его моделировании. Рассмотрим следующие виды моделей: стационарные и нестационарные; динамические; линейные и нелинейные; распределенные и сосредоточенные в пространстве; непрерывные и дискретные во времени; непрерывные и дискретные по величине; детерминированные и случайные; информационные.

Стационарные и нестационарные модели. Если свойства преобразо-

вания входных сигналов (функций), т.е. структура и свойства оператора А , не изменяются со временем, то систему и ее модель называют стационарной; в противном случае – нестационарной. Реакция стационарной системы на любой заданный тип возмущения зависит только от интервала времени между моментом начала действия входного возмущения и данным моментом време-

42

ни, т.е. свойство стационарности означает, что процесс преобразования входных сигналов (функций) инвариантен относительно сдвига как от текущего времени, так и от момента приложения входного сигнала. Реакция нестационарной системы зависит как от текущего времени, так и от момента приложения входного сигнала. В этом случае при сдвиге входного сигнала во времени (без изменения его формы) выходные сигналы не только сдвигаются во времени, но и изменяют свою форму.

Пример стационарной и нестационарной модели. Ко входу линии пере-

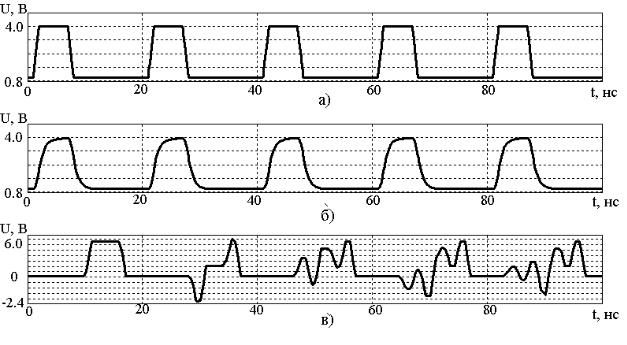
дачи длиной 50 м приложено импульсное напряжение с амплитудой 4В, частотой 50 МГц и длительностью импульса 5 нс (рисунок 2.25, а). Для исследования линии передачи с потерями используем соответствующую модель, встроенную, например, в программу схемотехнического моделирования MicroCAP 7 [9]. Рассмотрим два случая. В первом случае линия передачи обладает погонным сопротивлением 0.2 Ом/м, погонной емкостью 3.65 пФ/м и пренебрежимо малой погонной индуктивностью. Во втором случае линия передачи обладает такими же значениями R, C и погонной индуктивностью 9.13 нГн/м. По этим данным аналитически рассчитывается комплексный коэффициент передачи линии. Анализ переходных процессов производится с помощью интеграла свертки с импульсной характеристикой линии, которая вычисляется как преобразование Фурье коэффициента передачи.

В итоге модель линии передачи с пренебрежимо малой погонной индуктивностью представляет собой стационарную модель (рисунок 2.25, б) – свойства преобразования входных сигналов не изменяются со временем. Модель линии передачи с конечным значением погонной индуктивности демонстрирует свойства нестационарной модели (рисунок 2.25, в) – выходной сигнал не только изменяет свою форму с каждым периодом (появление новых гармоник), но и сдвигается по фазе.

К стационарным моделям можно обычно отнести и модели одномоментные, используемые в тех случаях, когда моделируется система, для которой необходимо получить какое-то решение в определенный момент времени. Примером могут служить системы управления запасами комплектующих, в которых одномоментные модели применяются повсеместно (определение однократного объема заказа на пополнение электрорадиоэлементов или времени подачи заказа).

Частным случаем стационарных моделей являются модели статические, которые включают описание связей между основными переменными процесса в установившихся режимах (в равновесном состоянии без изменения во времени). Например, математическое описание статики электротеплодинамического процесса состоит обычно из трех видов уравнений: электрического, материального и теплового балансов, термодинамического равновесия системы (характеристика движущей силы) и скоростей протекания процессов. Линейная подсистема РЭС, представленная на рисунке 2.22, также является типичным представителем статических моделей. Для расчетов медленных процессов или процессов, протекающих с небольшими отклонениями

43

от стабильных условий, принимается допущение, позволяющее считать процесс стационарным. Подобное допущение принимается, например, для расчета теплового баланса РЭС с достаточно большим значением постоянной времени.

а) – импульсы входного напряжения;

б) – импульсы выходного напряжения в линии с R = 0.2 Ом/м, С = 3.65 пФ/м,

L 0;

в) – импульсы выходного напряжения в линии с R = 0.2 Ом/м, С = 3.65 пФ/м,

L = 9.13 нГн/м

Рисунок 2.25 – Распространение сигнала в линиях передач с потерями

Стационарные математические модели (кроме статических) обычно состоят из дифференциальных уравнений, статические – из уравнений алгебраических.

Динамические модели позволяют рассчитать стационарные или нестационарные режимы объектов. Стандартные динамические модели включают переменные и соотношения между ними:

1)вектор независимых переменных Х;

2)добавочную независимую переменную t, называемую временем, хотя она может не представлять физическую временную размерность;

3)вектор неизвестных параметров ;

4)вектор переменных Y состояния системы, который является функцией от t, X и .

Эти функции, например, определяются неявно с помощью системы обыкновенных дифференциальных уравнений первого порядка

Y = dY/dt = h(t, X, Y, ),

44

где Х – вектор заданных функций, и системы начальных условий Y(0) = Y0(X,). Здесь Y0 – вектор заданных функций;

5) вектор наблюдаемых переменных Z, точными значениями которых Zт являются заданные функции от переменных состояния и от других перемен-

ных: Zт = Zт(t, X, Y, ).

Общеизвестный специальный случай – когда переменные состояния наблюдаются непосредственно, т.е. Z = Y.

Стандартные динамические модели характеризуются множеством переменных состояния системы, которые изменяются со временем (или в зависимости от некоторой другой независимой переменной) в соответствии с определенными дифференциальными уравнениями первого порядка. Начальные условия могут быть известны полностью или частично. Состояние системы наблюдается в различные моменты времени, но иногда переменные состояния не являются непосредственно измеряемыми, и вместо них приходится измерять связанные с ними наблюдаемые переменные. Неизвестные параметры могут появляться в начальных условиях, в дифференциальных уравнениях и в уравнениях наблюдений. В последнем случае они представляют неизвестные характеристики измерительных приборов, например константы калибровки.

Если в модели объекта содержатся дифференциальные уравнения порядка выше первого, сложность их анализа возрастает с ростом порядка уравнения (или с ростом числа дифференциальных уравнений в системе, поскольку уравнение m-го порядка можно преобразовать в систему из m уравнений 1- го порядка). Другая трудность, возникающая иногда при анализе систем дифференциальных уравнений, связана с особенностями задания начальных условий. Чаще всего начальные условия задаются при одном и том же значении независимой переменной. Для протекания переходного процесса в колебательном контуре, например, начальными условиями обычно служат значения напряжения на обкладках конденсатора и тока в индуктивности в один и тот же момент t = 0; в описаниях сглаживающего фильтра – это амплитуда и частота в одной и той же точке – на входе в устройство. Задачи с начальными условиями, заданными таким образом, называются задачами Коши. Моделировать их сравнительно просто.

Но встречаются задачи, в которых различные начальные условия заданы в разных точках. Например, при расчете тепловых режимов РЭС часть условий может быть задана со стороны входа одного теплового потока, часть

– со стороны входа другого. Это краевые задачи. Если краевую задачу не удается свести к задаче Коши с помощью дополнительных уравнений, то решение усложняется. При этом требуется, как правило, применение специальных расчетных приемов – итерации и др.

Состояние системы можно представить как точку с координатами y1, y2, в некотором пространстве m измерений, называемом фазовым про-

45

странством или пространством состояний. Эта точка называется изображающей. Изменению состояния системы отвечает некоторое движение изображающей точки в этом пространстве. Путь изображающей точки при этом есть интегральная кривая системы. Эта кривая носит название фазовой траектории.

При построении фазового пространства добиваются взаимно однозначного и непрерывного соответствия между состояниями системы и точками фазового пространства, т.е. каждому состоянию системы должна соответствовать одна и только одна точка фазового пространства, а каждой точке фазового пространства – одно и только одно состояние системы. При этом близким состояниям системы должны соответствовать близкие точки фазового пространства. В силу этих требований фазовое пространство не всегда может быть обычным евклидовым m-мерным пространством.

Пример двойственности динамических моделей. Рассмотрим физиче-

ский маятник, состояние которого характеризуется угловой скоростью S и углом отклонения от состояния устойчивого равновесия. Уравнение движения маятника при отсутствии сопротивлений dS/dt = –a sin ; d/dt = S, где a = const определяется конструкцией маятника. Фазовое пространство в данном случае двумерно. Если принять, что оно является плоскостью, на которой осии S – соответственно оси абсцисс и ординат, то состояние системы с одинаковыми угловыми скоростями S и со значениями = + 2 – при произвольном и сколь угодно малом будут сколь угодно близки. Однако соответствующие им точки плоскости будут отстоять одна от другой на расстоянии 2 – , которое при 0 не стремится к нулю. При таком выборе фазового пространства нарушены как требование взаимной однозначности, так и требование непрерывности соответствия состояния системы точкам фазового пространства. Чтобы удовлетворить этим требованиям, необходимо взять за фазовое пространство цилиндрическую поверхность с осью S, направленной по образующей, и с угловой координатой .

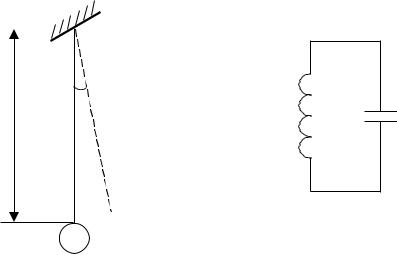
Приведенные выше уравнения для малых колебаний маятника (рисунок 2.26, а) преобразуются в дифференциальное уравнение второго порядка

a d 2 0 , dt 2

где а – постоянный множитель.

Аналогично анализ процессов в электрическом колебательном контуре (рисунок 2.26, б) сводится к исследованию дифференциального уравнения

где q – мгновенное значение заряда на обкладках конденсатора. Из последнего уравнения можно получить все сведения об исследуемом процессе, например, период электрических колебаний

T 2 LC .

46

Из сравнения дифференциальных уравнений маятника и контура следует, что они по существу одинаковы. Таким образом, совершенно разные явления могут описываться моделями в виде дифференциальных уравнений одного и того же вида, а именно – дифференциальными уравнениями второго порядка

Здесь y – обобщенная координата, определяющая состояние движения системы; a0, a1, a2 – коэффициенты, зависящие от параметров системы. В случае маятника обобщенной координатой является угол отклонения от вертикали, в случае колебательного контура – заряд конденсатора.

m

а – маятник; б – электрический контур

Рису нок 2.26 – Простейшие динамические объекты

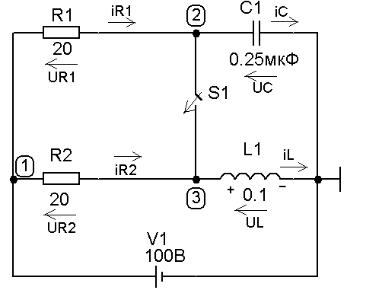
Пример динамической модели. На рисунке 2.27 представлена динамическая модель подсистемы РЭС. Требуется с помощью этой модели оценить характер изменения напряжения на емкости С1 и тока индуктивности L1 в результате замыкания ключа S1.

Определение начальных условий. В нулевой момент времени (t = 0) ключ в схеме разомкнут. Ток в ветви R1C1 не протекает, емкость С1 заряжена

до напряжения источника питания V1, т.е. UC(0) = 100 В. Ток индуктивности

в начальный момент времени равен IL(0) = V1/R2 = 5А.

Составление систем уравнений, описывающих поведение схемы. Уравнение равновесия: IR1 + IR2 – IC – IL = 0.

V1 U R2 U L 0;

Уравнения непрерывности: U R1 U R2 0;U C U L 0.

47

Рисунок 2.27 – Динамическая модель подсистемы РЭС

После преобразования получаем математическое описание динамической модели подсистемы РЭС:

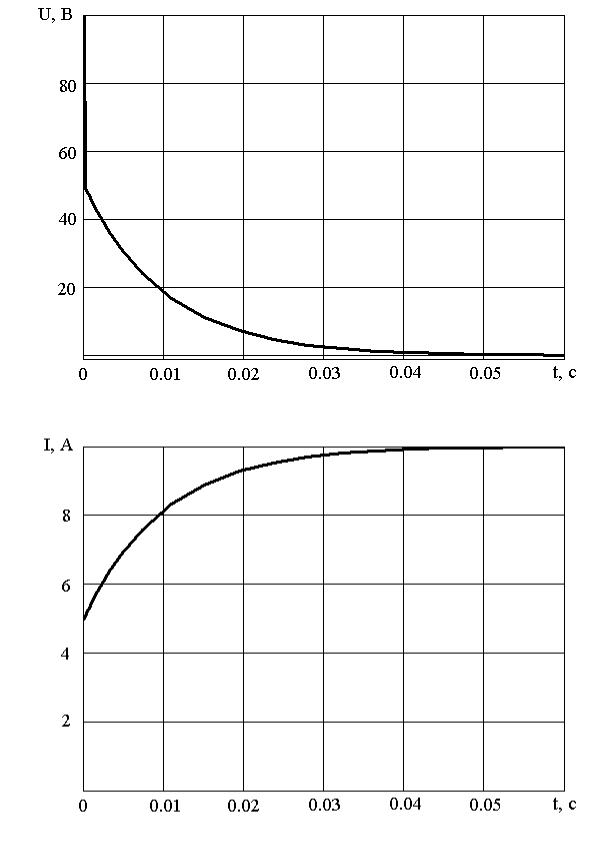
Результаты моделирования в программе MathCAD 2001 [10] представлены на рисунке 2.28. После замыкания ключа напряжение на емкости мгновенно падает до 50 В, затем по экспоненциальному закону снижается до нуля (разряд емкости). Ток индуктивности по экспоненциальному закону возрастает с 5 до 10 В. Время переходного процесса составляет около 0.05 с.

49

Линейные и нелинейные модели. Линейность или нелинейность анализируемого процесса оказывает решающее влияние на вид модели, метод программирования и быстродействие программы при ее выполнении на ЭВМ. Благодаря быстродействию и простоте линейные модели широко применяются разработчиками, хотя большинство природных и промышленных процессов – нелинейно. Примером линейной модели является зависимость между напряжением и силой тока в электрической цепи, хотя это справедливо в ограниченном диапазоне токов и напряжений.

Линейность или нелинейность по отношению к входным сигналам – это не то же самое, что линейность или нелинейность выходных переменных (функций) по параметрам. Оператор А и задаваемая им модель называются линейными, если для системы справедлив принцип суперпозиции. Он состоит в том, что линейной комбинации произвольных входных сигналов ставится в соответствие та же линейная комбинация сигналов на выходе из системы:

Математическую модель с использованием линейного оператора можно представить в виде = АХ.

Нелинейные уравнения, в свою очередь, можно разделить на два подкласса: алгебраические (в которых над переменными производятся только действия сложения, вычитания, умножения, деления и возведения в степень с рациональным показателем) и трансцендентные, в которые входят другие функции от переменных (показательные, тригонометрические и др.). В любом случае сложность модели существенно зависит от числа уравнений и от вида входящих в них функций. Обычно наиболее просто решаются алгебраические уравнения 1-й степени (линейные), наиболее сложно – трансцендентные.

В математических моделях часто используется ряд нелинейных математических структур, в первую очередь, это степенные полиномы. Методы интерполяции дают возможность существенно упростить способы расчета коэффициентов степенного полинома при наличии точных данных о входных и выходных параметрах. Например, при выборе в качестве математической структуры полинома вида

P(x) = a0 + a1(x – x0) + a2(x – x0)(x – x1) + … + an + 1(x – x0)…(x – xn)

для данных с равноотстоящими значениями независимой переменной коэффициенты рассчитываются по упрощенному способу:

a0 = y0; ai i yi0 , i = 1, 2, …, n, i!h

где h – шаг интерполяции; iy0 – разность i-го порядка. В результате полином P(x) записывается в виде