Кислицын А.А. 
Физика атома, атомного ядра 
и элементарных частиц
10 (1). Простейшая задача квантовой
механики:
частица в "потенциальной яме" ("ящике"). 
Квантовые точки. 
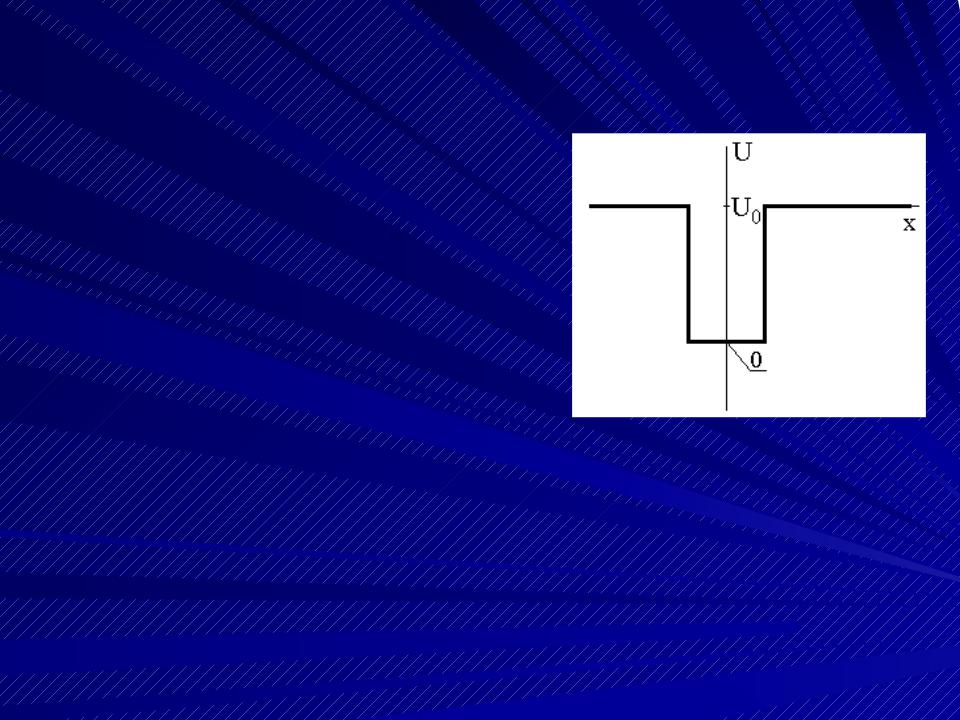
Одномерная прямоугольная потенциальная яма ("ящик")
Так называется одномер- ная область, в которой потенциальная энергия
имеет вид, изображен-
ный на рисунке. Для этой области легко получить
точное решение уравне-
ния Шредингера и рас- смотреть задачу о кван-
товании энергии.
Потенциальная энер- 
гия равна нулю на
дне ямы ("ящика"),
и равна U0 вне сте- нок "ящика".
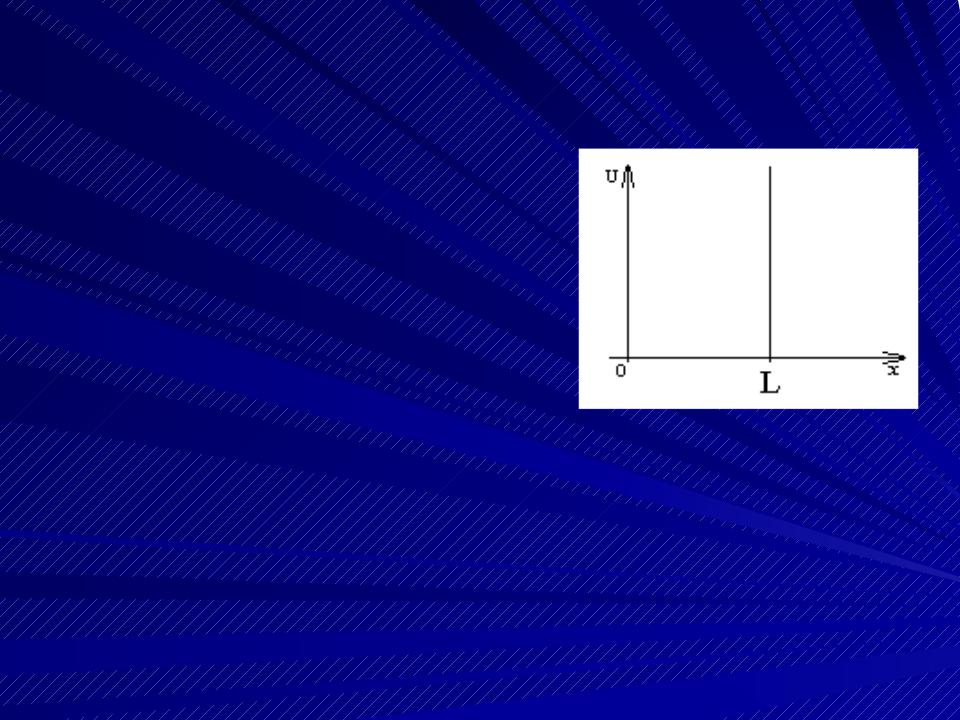
Одномерная прямоугольная потен-
циальная яма (ящик) с бесконечно высокими стенками
Наиболее простым в мате-
матическом отношении является решение для по-
тенциальной ямы с беско-
нечно высокими стенка- ми. Иногда ее называют ямой с идеально отража- ющими стенками.
0, 0 x L U , x 0, x L
Ширина ямы (ящика)
равна L, высота сте-
нок бесконечно ве- лика. На дне ямы по-
тенциальная энергия
равна нулю.
В этом случае внутри ямы частица дви-
жется свободно, но выйти за ее преде-
лы не может, т.е. за пределами ямы
волновая функция должна обратиться в
нуль. Но волновая функция должна быть непрерывна, поэтому она должна
быть равна нулю в точках x = 0 и x = L:
(0) (L) 0 |
(10.1) |
- это граничные условия для волновой функции . 
Стационарное уравнение Шредингера
(9.6) |
2m |
(E U ) 0 |
|
|
|
|
|||
|
2 |
|
|
|
внутри ямы принимает вид (т.к. U = 0): |
||||
d 2 |
2m |
|
||
dx2 |
|
|
2 E 0 |
(10.2) |
Общее решение этого уравнения хорошо известно:
(x) Asin |
2Em |
x B cos |
2Em |
x (10.3) |
|
|
|||
|
|
|
||
Из условия (10.1) (0) =0 следует, что B = 0.
Из второго граничного условия (L) = 0 сле- 
дует, что |
Asin |
|
2Em |
L 0 |
|
|||||
|
|
|
||||||||
|
|
|
|
|
||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
2Em |
|
L n |
|
|||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
или |
|
|
2Em |
|
n |
|
(10.4) |
|||
|
|
|
|
|
|
L |
||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|||||
где n = 1, 2, 3, ... - целое число
Таким образом, собственными функция-
ми уравнения Шредингера в рассматри-
ваемой задаче являются волновые |
|
||
функции вида |
|
||
n An sin n x |
(10.5) |
||
|
|
L |
|
Собственные значения энергии найдем из |
|||
формулы (10.4): |
|
||
En |
2 2 |
n2 |
(10.6) |
|
|||
|
2mL2 |
|
|
- дискретный спектр собственных значений энергии. 
Коэффициент An определим и из условия нормировки (7.2):
|
|
2 |
2 |
|
|
|
2 nx |
|
1 |
2 |
l |
|
|
|
|
2 nx |
|
|
|
An |
|
|
|
dx |
|
An |
|
1 cos |
|
dx |
|||||
|
ndx 1 |
|
|
sin |
L |
2 |
|
|
L |
||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
A L 1 |
|
A |
|
|
|
|
|
|
||||
|
|
|
|
|
L |
|
|
||||||||||
|
|
|
|
|
n |
|
|
|
n |
|
|
|
|
|
|||
т.е. нормирующий множитель у всех собст- венных функций одинаков. Поэтому
n |
2 |
sin |
nx |
(10.8) |
|
L |
|||
|
L |
|
||
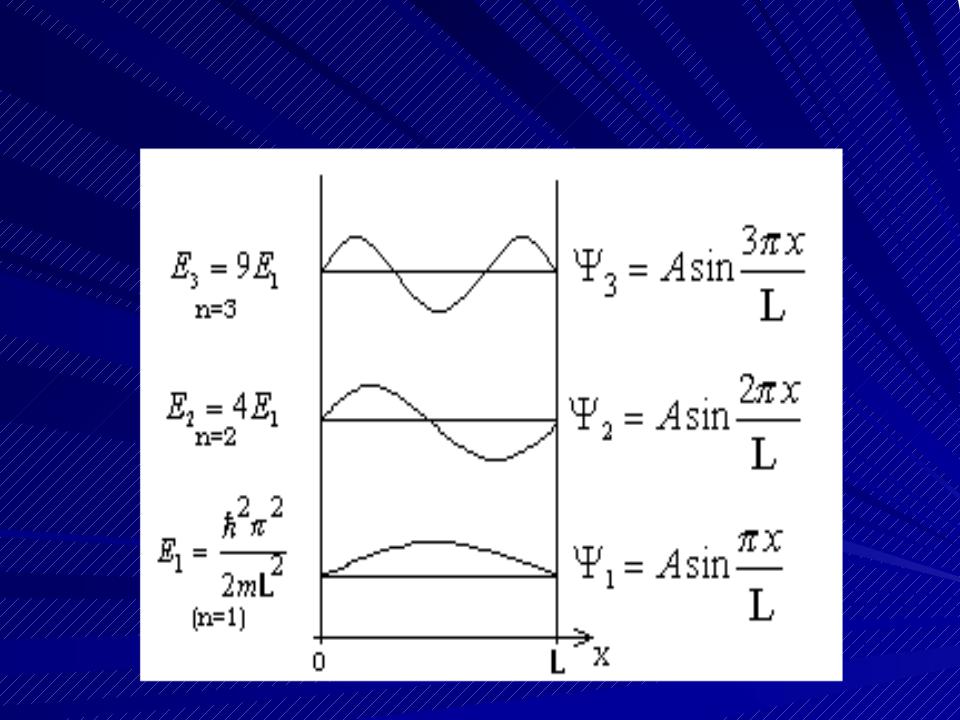
Графики первых трех собственных функций
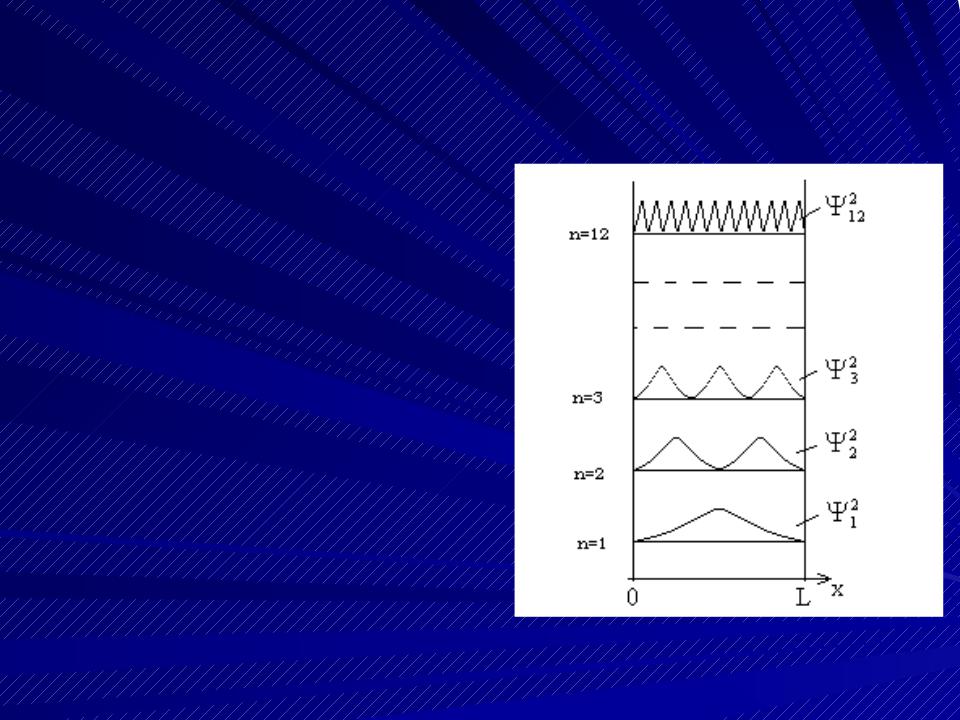
Плотность вероятности распределения частиц
По физическому смыслу квадрат модуля собст- венной функции – это плотность вероятности распределения частиц по пространству. В низшем состоянии с наибольшей
вероятностью можно най- ти частицу около середи- ны ящика; вероятность найти ее у стенок равна
нулю.