Кислицын А.А. Физика атома, атомного ядра и элементарных частиц
6. (1). Фазовая и групповая скорость
волн де-Бройля. Волновой пакет.
ФАЗОВАЯ СКОРОСТЬ
Плоская монохроматическая волна с амплитудой А, частотой и волновым вектором k может быть
представлена в комплексной форме в виде: |
|
|||
r,t Ae i t k r |
Ae |
i |
Et p r |
|
|
(6.1) |
|||
Фазовой скоростью волны называется скорость, с которой движутся точки волны с постоянной фа-
зой. Если ось x направлена по вектору p, то усло-
вие постоянства фазы
Et - px = const. |
(6.2) |
Чтобы вычислить фазовую скорость, надо продиф- ференцировать это уравнение по времени.
|
|
|
|
|
|
|
|
|
|
|
|
dx |
Продифференцируем (6.2) по времени: |
E p dt 0 |
|||||||||||
|
|
|||||||||||
откуда dx |
E , где |
dx |
vф - фазовая скорость. |
|||||||||
dt |
p |
|
dt |
|
|
|
|
E |
|
|
|
|
По формулам (5.2) и (5.3) находим: |
|
|||||||||||
|
|
|
|
|
|
|
|
|
p |
|
k |
k |
С другой стороны: |
E |
|
mc2 |
|
c2 |
|
|
|
|
|||
p |
mv |
v |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
где v - скорость частицы. |
|
|
|
|
|
|
|
|
|
|||
Итак, фазовая скорость: |
|
vф |
|
|
c2 |
(6.3) |
||||||
|
k |
|
v |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Суперпозиция волн
Рассмотренная выше плоская монохроматическая волна представляет собой строго периодический 
процесс, бесконечно протяженный в пространстве и во времени. Это абстракция: ни в природе, ни в технике такие волны не существуют. Любой реаль- ный процесс имеет начало и конец, он ограничен как во времени, так и в пространстве и не являет- ся строго гармоническим. Его можно рассматри- 
вать как результат суперпозиции (наложения) 
некоторого количества монохроматических волн, которые вследствие интерференции в одних час- тях пространства усиливают друг друга, а в других - гасят друг друга. 
Образование волновой группы
Рассмотрим простейший случай: суперпозицию двух
волн u1 a cos 1t k1x , u2 a cos 2t k2 x
распространяющихся вдоль оси x. Будем считать,
что частоты 1 и 2, а также абсолютные значения волнового вектора k1 и k2 очень мало отличаются
друг от друга. Складывая u1 и u2, находим:
u u1 u2 a cos 1t k1x a cos 2t k2 x
|
|
|
1 |
2 |
|
k1 k2 |
|
|
1 2 |
|
|
k1 k2 |
|
||||||
|
2a cos |
|
|
|
|
t |
|
|
x |
cos |
|
|
|
t |
|
|
x |
||
|
2 |
|
2 |
|
|
2 |
|
2 |
|||||||||||
Обозначим: |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
k1 k2 |
|
|
|
|
|
|
|
|
k1 k2 k |
||||||||
|
1 2 |
, |
k, |
1 2 |
|
|
, |
||||||||||||
2 |
|
2 |
|||||||||||||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
2 |
2 |
|||||
Тогда |
|
|
|
u 2a cos |
2 |
|
|
|
Результат изобра-
жен на рисунке.
Получились вол- новые группы, движущиеся с оп-
ределенной скорос-
t |
k |
|
cos t |
2 |
x |
||
|
|
|
тью вдоль оси x. Т.к. частоты и волновые очень мало различаются, можно считать,
вый множитель в (6.4): |
|
|
t |
k |
|
||||
|
2a cos |
2 |
2 |
|
|
|
|
kx |
(6.4) |
|
числа что пер-
|
(6.5) |
x |
|
|
|
представляет собой медленно меняющуюся ампли- туду модулированной волны. 
ГРУППОВАЯ СКОРОСТЬ
Скорость перемещения волновой группы - это ско-
рость перемещения определенной амплитуды. Для ее определения запишем условие постоянст-
ва амплитуды: |
|
t |
k |
x const |
(6.6) |
|
2 |
2 |
Дифференцируя (6.6) по t, получаем скорость пере-
мещения волновой группы: |
vгр dx |
|
|
|
|
|
dt |
k |
В пределе k 0 получаем формулу для груп-
повой скорости:
vгр d
dk
ГРУППОВАЯ СКОРОСТЬ ВОЛН ДЕ-БРОЙЛЯ Для волн де-Бройля:
vгр |
d |
|
d |
|
|
dE |
|
d c p2 m02c2 |
|
|||||
dk |
d k |
dp |
|
|
dp |
|||||||||
|
|
|
|
|
|
|
(6.8) |
|||||||
|
|
|
|
cp |
|
|
|
c2 p |
|
c2mv |
|
|||
|
|
|
|
|
|
|
|
v |
|
|||||
|
p2 m02c2 |
|
E |
|
mc2 |
|
||||||||
|
|
|
|
|
|
|
|
|||||||
Таким образом, "обычная", т.е. измеряемая в
эксперименте скорость частицы v равна групповой скорости волн де-Бройля vгр
СООТНОШЕНИЕ МЕЖДУ ФАЗОВОЙ И ГРУППОВОЙ СКОРОСТЬЮ ВОЛН ДЕ-БРОЙЛЯ
Вернемся к формуле (6.3) и запишем ее в виде
vф c2 |
c c |
vф v c2 |
или |
v |
v |
|
|
Из этой формулы следует, что фазовая скорость волн де-Бройля всегда больше скорости света (т.к.
скорость частицы v всегда меньше скорости све- та). Это, однако, не противоречит теории относи- тельности, т.к. фазовая скорость не характеризует ни скорость перемещения массы, ни скорость пе- ремещения энергии. 
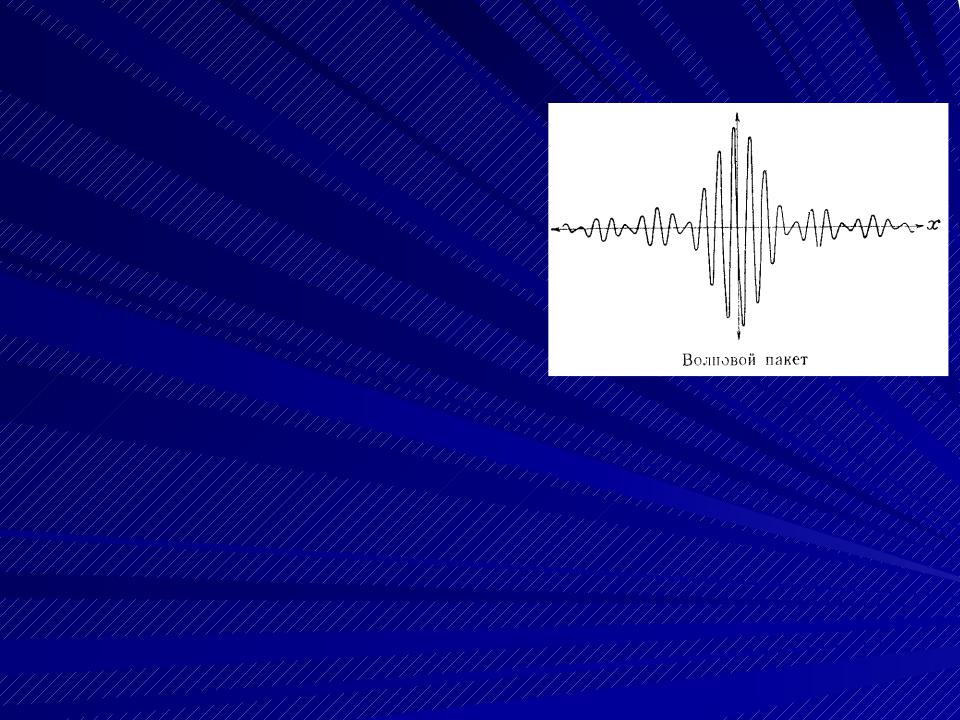
ВОЛНОВОЙ ПАКЕТ
Путем наложения (супер-
позиции) плоских волн с
непрерывно меняющими-
ся волновыми числами можно осуществить такой
волновой процесс, при ко- тором амплитуда волны будет заметно отли- 
чаться от нуля только в небольшой части 
пространства, а в остальном пространстве бу-
дет почти равна нулю. Такой волновой про- цесс называется волновым пакетом.