Лекция 2 ИНФОРМАЦИОННЫЕ ХАРАКТЕРИСТИКИ ИСТОЧНИКОВ СООБЩЕНИЙ

2.1 Определение количества информации

2.2. Информационные характеристики источников дискретных сообщений

2.3 Информационные характеристики источников непрерывных сообщений

2.1 Определение количества информации

Модели, используемые в теории информации

Понятие информация тождественно понятию сведения или сообщения и ассоциирует с наличием по крайней мере двух взаимодейст­вующих систем А и В (рис.1.1), одна из которых А является источником информации (передатчиком), а вторая В является наблю­даемой системой (приемником). Вне указанной схемы понятие «информация» те­ряет смысл.

Сообщение — это то, что можно сообщить, а сообщить можно только состояние системы. Следовательно, сообщение — это состояние системы.

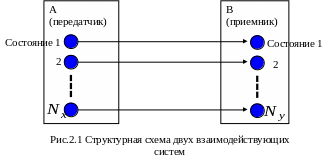
Любая система описывается совокупностью физических величин, которые могут зависеть от параметров. Состояния системы — это значения физической величины или парамет­ра (изображение, звук, текст и т.д.), которые ее описывают. Например, имеется передатчик, вырабатывающий аналоговый сигнал, фрагмент реализации которого представлен на рис.1.2. Данный сигнал подвергается дискретизации по времени и квантованию по уровню. Разрешенные уровни как раз и являются состояниями источника.

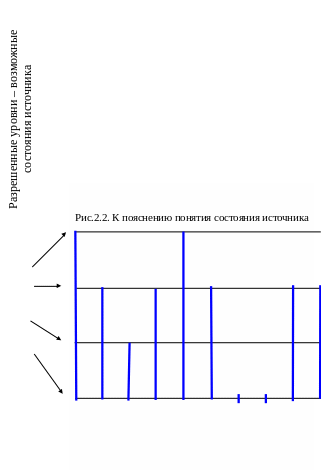
Для данного примера количество возможных состояний источника равно четырем.

В качестве другого примера можно привести источник, вырабатывающий текст, состоящий из букв какого-либо языка. Буквы данного языка вместе с разделительными знаками и пробелом будут являться возможными состояниями для данного источника.

Система случайным образом с некоторой вероятностью может оказаться в том или другом состоянии (передатчик приходит в состояние, которое соответствует передаваемому символу). Следовательно, множество состояний системы можно рассматривать как множество случайных событий. Две системы будем называть статистически зависимыми, если состояние одной из них влияет на вероятность состояния другой.

Множества состояний Х и Y, соответственно систем А и В, в зависимости от того, в каком отношении они рассматри­ваются, можно интерпретировать как множества состояний, сообщений и событий.

Два множества Х и Y с заданным на них двумерным рас­пределением пред­ставляют собой модель двух взаимодействующих систем. Эта модель лежит в основе построения статистической теории информации.

Сигнал — это материальный переносчик информации в пространстве и во времени.

Сигналы могут быть динамическими и статическими. Динамические сигналы предназначены для передачи информации в пространстве (электромагнитная волна). Статические сигналы (запоминающие устройства) предназначены для передачи информации во времени (компакт-диск, кинофильм и т.д.). Точнее, сигналом является не сам материальный переносчик информации, а его состояние. Поэтому целесообразно конкретизировать опреде­ление сигнала.

Сигнал — это значение физической величи­ны, которое отображает состояние источника сообщений. Поскольку множество сообщений можно рассматривать как множество случайных событий, то отображающее значение физической величины также будет случайным.

Следовательно, случайную величину можно принять в качестве модели сигнала. В общем случае состояние системы (передаваемое сообщение) изменяется во времени, поэтому указанная случайная величина также будет изменяться во времени, зависеть от времени. Случайная величина, завися­щая от времени (некоторого параметра), называется слу­чайным процессом. Следовательно, случайный процесс является моделью сигнала.

В соответствии с решением вопроса установления меры количества и качества информации в теории информации выделяют три основные направления: структурное, статистическое и семантическое.

Структурная теория рассматривает дискретное строение массивов информации и их измерение простым подсчетом информационных символов; применяется для оценки предельных возможностей информационных систем вне зависимости от условий их применения.

Статистическая теория оперирует понятием «энтропия» как мерой неопределенности или неожиданности, учитывающей вероятность, а, следовательно, информативность сообщений; применяется для оценки информационных систем в конкретных условиях их применения.

Семантическая теория учитывает целесообразность, ценность, полезность или существенность информации; применяется для оценки эффективности логического опыта.

Остановимся на рассмотрении мер информации в первых двух теориях.

Комбинаторное определение количества информации

Среди структурных мер наиболее распространенной является мера Хартли, впервые выдвинутая им в 1928 г., в виде комбинаторного определения количества информации. Это определение предполагает модель с детерминированной связью (помехи отсутствуют) между дискретными состояниями двух систем без их вероятностного описания.

До получения сведений о состоянии системы имеется ап­риорная неопределенность ее состояния. Сведения позволяют снять эту неопределенность, то есть определить состояние системы. Поэтому количество информации можно определить как меру снятой неопределенности, которая растет с ростом числа состояний системы.

Количественная мера информации устанавливается сле­дующими аксиомами.

Аксиома 1. Количество информации, необходимое для снятия неопределенности состояния системы, представляет собой монотонно возрастающую функцию числа состояний системы.

В качестве количественной меры информации можно вы­брать непосредственно число состояний системы N_x, которое является единственной характеристикой множества X.

Однако такое определение не удобно с точки зрения его практического применения. Поэтому в теории информации вводится несколько иная количественная мера информации, которая является функцией N_х. Вид указанной функции по­зволяет установить аксиома 2.

Аксиома 2. Неопределенность состояния сложной системы, состоящей из двух подсистем, равна сумме неопределен­ностей подсистем.

К количественной мере информации естественно выдвинуть следующие требования:

1. Количество информации в сообщении о достоверном событии равно нулю.

2. Количество информации, содержащееся в двух независимых сообщениях, должно равняться сумме количества информации в каждом из них, то есть мера информации должна быть аддитивной величиной.

3. Количество информации не должно зависеть от качественного содержания сообщения. То есть от степени важности или полезности для получателя.

В соответствии с требованием 2, если для снятия неопределенности первой подсистемы необходимо количество информации, равное I(N₁), а для второй подсистемы количество информации, равное I(N₂), то для снятия неопределенности сложной системы необходи­мо количество информации, равное

I(N₁N₂) = I(N₁) + I(N₂) , (1.1)

где N₁ — число состояний первой подсистемы; N₂ — число состояний второй подсистемы; N₁ N₂—число состояний слож­ной системы.

Единственным решением полученного функционального уравнения является логарифмическая функция

I= log_а N,

которая определяет количество информации как логарифм числа состояний системы. Основание логарифма а опреде­ляет единицу измерения количества информации. В зависи­мости от значения а единицы измерения называются двоич­ными (а=2), троичными (а=3) и в общем случае а-ичными. В дальнейшем под символом log будем понимать двоичный логарифм.

Каждое передаваемое слово из п букв, записанное в ал­фавите, содержащем N букв, можно рассматривать как отдельное «укрупненное» состояние источника сообщений. Всего таких состояний (слов) будет

. (1.2)

Это информационная емкость, или количество информации в сообщении, характеризующая его потенциальное структурное разнообразие.

Структурная мера (мера Хартли) количества информации определяется

. (1.3)

Выбор основания логарифма а несущественен, так как переход от одной системы логарифмов к другой сводится лишь к умножению логарифма с данным основанием на соответствующий множитель. Он равен 1,443 при переходе от натуральных логарифмов к двоичным и 3,32 при переходе от десятичных логарифмов к двоичным. При использовании десятичных логарифмов количество информации определяется в десятичных единицах - дитах. Дитами удобно пользоваться при анализе процессов в приборах, работающих в десятичной системе счисления. При использовании натуральных логарифмов единицей измерения является натуральная единица – нит. В случае использования двоичных логарифмов количество информации измеряется в двоичных единицах - битах.

При а=2 за единицу информации принято количество информации, которое содержится в сообщении из одного элемента ( =1), принимающего одно из двух равновероятных значений (N=2), т.е. . Эта единица измерения называется «БИТ» (сокращенно от английского термина «binary unit» - двоичная единица).

Итак, количество информации в рассматриваемом случае равно логарифму длиной :

, [бит].

Известно, что всякая информация получается потребителем после принятия сообщения, т.е. в результате опыта. Сообщение, получаемое на приемной стороне, несет полезную информацию лишь в том случае, если имеется неопределенность относительно состояния источника сообщений. Количественной мерой неопределенности ситуации является энтропия. Термин и понятие энтропии по-разному вводится и используется в физике (термодинамике ) и кибернетике (теории информации) .

В теории информации энтропия рассматривается как мера неопределённости случайной величины. За количественную меру оценки неопределённости (Н) принимают среднее значение неопределённости появления каждого из возможных сообщений (состояний, событий). Математически отображается в следующем виде:

, бит.эл. (1.4)

При N=1 Н=0, т.е. количество информации в сообщении, элементы которого могут принимать лишь одно значение, равно нулю.

Необходимо отметить, что структурная мера (мера Хартли) количества информации не связана со смыслом передаваемого сообщения (семантикой) и тем влиянием, которое оно может оказать на получателя сообщения.

Пусть, например, информационная емкость некоторой системы равна тысяче: Q=10³, I=log₂10³=3log₂1010 [бит], это значит, что в двоичной системе данное число можно закодировать 10 разрядным числом, т.е. для его описания достаточно 10 бит.