
3. Математическая модель процесса функционирования локомотива
У любой единицы тягового подвижного состава (для краткости будем употреблять термин локомотив, подразумевая под этим не только электровозы и тепловозы, но и электро- и дизель-поезда) в процессе эксплуатации могут возникать отказы двух типов.
Отказ первого типа, при возникновении которого работоспособное состояние локомотива восстанавливается локомотивной бригадой в пути следования.
Отказ второго типа, который требует для восстановления работоспособного состояния локомотива постановки его в депо (ПТОЛ) на плановый ремонт.
В процессе функционирования локомотив может находиться в следующих состояниях.
Локомотив находится в работоспособном состоянии и выполняет свои функции — работает.
Локомотив восстанавливается в пути следования после отказа первого типа.
Локомотив находится в ожидании внепланового ремонта после отказа второго типа.
Производится восстановление работоспособного состояния локомотива на внеплановом ремонте.
Ожидание начала эксплуатации после окончания внепланового ремонта.
Отстой по неравномерности движения.
Ожидание начала планового ремонта.
Плановый ремонт.
Ожидание начала эксплуатации после окончания планового ремонта.
Граф переходов локомотива из одного состояния в другое за бесконечно малый промежуток времени Δt при условии, что все временные параметры процесса функционирования локомотива являются случайными величинами, распределенными по экспоненциальному закону каждый со своей интенсивностью, показан на рис. 8.
Вероятности переходов локомотива из одного состояния в другое за бесконечно малый промежуток времени Δt записываются следующим образом:
![]() —вероятность
возникновения отказа первого типа;
—вероятность
возникновения отказа первого типа;
![]()
![]() , Tо—
среднее значение наработки на отказ
первого типа;
, Tо—
среднее значение наработки на отказ
первого типа;
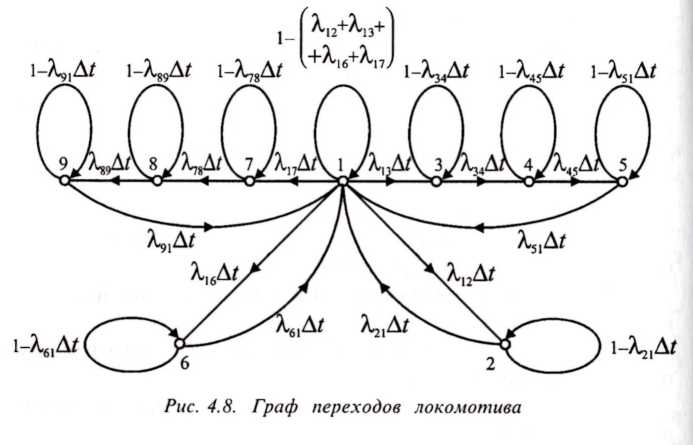
Рисунок 8– Граф перехода локомотива
![]() — вероятность возникновения отказа
второго типа;
— вероятность возникновения отказа
второго типа;
![]() —
вероятность восстановления
работоспособности после
—
вероятность восстановления
работоспособности после
![]() отказа
первого типа;
отказа
первого типа;
— среднее время восстановления работоспособности после отказа первого типа;
![]()
![]() —
вероятность постановки локомотива в
депо для проведения внепланового
ремонта;
—
вероятность постановки локомотива в
депо для проведения внепланового
ремонта;
— среднее время ожидания начала внепланового ремонта;
![]() — вероятность окончания внепланового
ремонта;
— вероятность окончания внепланового
ремонта;
— среднее время внепланового ремонта;
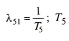
![]() — вероятность выдачи локомотива в
эксплуатацию после внепланового
ремонта;
— вероятность выдачи локомотива в
эксплуатацию после внепланового
ремонта;
— cреднее время ожидания начала эксплуатации после внепланового ремонта;
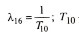
![]() —вероятность
постановки локомотива в отстой по
неравномерности движения;
—вероятность
постановки локомотива в отстой по
неравномерности движения;
-средняя продолжительность работы локомотива до постановки в отстой;
![]()
![]() — вероятность окончания отстоя (выдачи
локомотива в эксплуатацию);
— вероятность окончания отстоя (выдачи
локомотива в эксплуатацию);
— среднее значение времени отстоя;
![]()
![]() — вероятность изъятия локомотива из
эксплуатации для проведения планового
ремонта;
— вероятность изъятия локомотива из
эксплуатации для проведения планового
ремонта;
–средняя продолжительность работы локомотива до постановки на
плановый ремонт;
![]()
![]() — вероятность постановки локомотива
в депо для проведения планового
ремонта;
— вероятность постановки локомотива
в депо для проведения планового
ремонта;
— среднее время ожидания начала планового ремонта;
![]() — вероятность окончания планового
ремонта;
— вероятность окончания планового
ремонта;
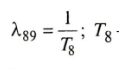
— средняя продолжительность планового ремонта;
![]()
![]() — вероятность выдачи локомотива в
эксплуатацию после планового ремонта;
— вероятность выдачи локомотива в
эксплуатацию после планового ремонта;
— среднее время ожидания начала эксплуатации Т9
после планового ремонта.
Уравнения Колмогорова (9), связывающие между собой вероятности состояний локомотива в моменты времени t и t + Δt, записываются в следующем виде:

(22)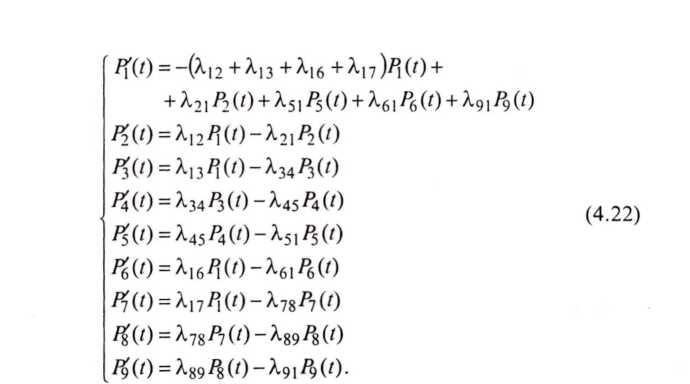
Задавшись
начальными условиями ![]() ,
, ![]()
решим полученную систему дифференциальных уравнений и найдем зависимости Pi{t), t = 1-9.
Однако для практики наибольший интерес представляет доля времени, в течение которого локомотив находится в каждом из состояний при длительной эксплуатации, т.е. при t →∞Поскольку граф переходов локомотива (см. рис. 8) является связным, то у процесса функционирования локомотива существует установившийся режим, в котором вероятности всех состояний перестают зависеть от времени и принимают финальные значения Рi = const, i = 1—9.
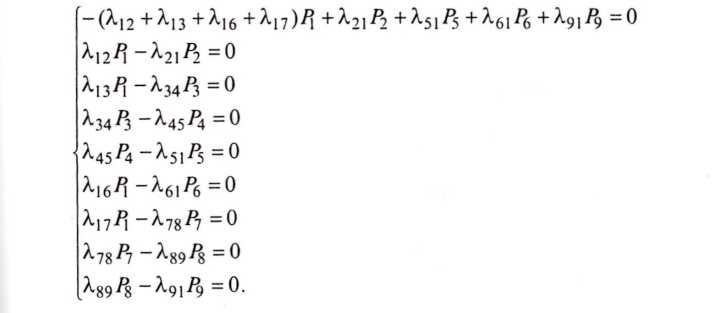 В
установившемся режиме система
дифференциальных уравнений (22)
превращается в систему алгебраических
уравнений:
В
установившемся режиме система
дифференциальных уравнений (22)
превращается в систему алгебраических
уравнений:
Решение этой
системы получается при условии![]()
![]() (23)
(23)
Для
решения выразим вероятности всех
состояний ![]() через вероятность первого состояния
Р1.
через вероятность первого состояния
Р1.
Подставив выражения всех вероятностей Р2 — Р9 в уравнение (23)
Решив это уравнение относительно P1
Вероятность
Р1
показывает долю времени, в течение
которого локомотив работоспособен и
используется по назначению, поэтому
ее называют коэффициентом использования
локомотива ![]() .
.
Выразив
все интенсивности через соответствующие
средние значения ![]()
Рассматриваемая
модель функционирования локомотива
превращается в рассмотренную выше
модель функционирования объекта с
двумя возможными состояниями, если
локомотив в процессе эксплуатации
будет иметь только отказы первого типа
и не будет иметь внеплановых и плановых
ремонтов, а также отстоев по неравномерности
движения, т.е. если![]()
Тогда
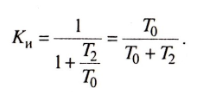
(24)
В этом случае формула (24) совпадает с формулой (21), выведенной для объектов с двумя состояниями, т.е. рассматриваемая модель функционирования локомотива является более общим случаем, из которого модель функционирования объектов с двумя состояниями выводится как частный случай.
Коэффициент готовности Кr представляет собой вероятность того, что локомотив окажется в работоспособном состоянии в произвольный, достаточно удаленный от начала эксплуатации момент времени. Локомотив работоспособен, если он находится в 1-м, 5, 6 или 9-м состоянии, т.е.
![]() (25)
(25)
П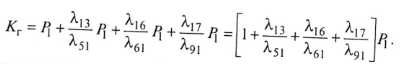 одставив
в (25) значения вероятностей
одставив
в (25) значения вероятностей ![]() ,
выраженные
через Р1,
получим
,
выраженные
через Р1,
получим
Выразив интенсивности X- через среднее значение соответствующих времен, а вероятность Р1 — по формуле (24)
Величина
![]() (26)
(26)
выраженная в процентах, показывает, какая часть локомотивов находится в неработоспособном состоянии, и является аналогом используемого в локомотивном хозяйстве ОАО «РЖД» показателя — общий процент неисправных локомотивов, который в 2000 г. составил в среднем по сети 10,6%. Расчеты по формуле (28) для разных локомотивных депо показывают, что коэффициент готовности находится в пределах 0,87—0,92, или в среднем составляет около 0,9, т.е. коэффициент Kн ≈ 0,1, что практически совпадает со значением общего процента неисправных локомотивов.
Однако
показатель — процент неисправных
локомотивов дает только общее
представление о том, какая часть
локомотивов находится в неработоспособном
состоянии, а kн,
рассчитанный по формулам (26) , раскрывает
связь этого показателя с параметрами
процесса функционирования локомотивов
![]() и
позволяет наиболее эффективно управлять
их состояниями, воздействуя на те
параметры
,
к которым наиболее чувствительны
эксплуатационные коэффициенты —
коэффициент технического использования
(24), коэффициент готовности (28), коэффициент
неработоспособности локомотивов (26).
Показателями чувствительности
являются значения частных производных
от эксплуатационных коэффициентов по
каждому из параметров
и
позволяет наиболее эффективно управлять
их состояниями, воздействуя на те
параметры
,
к которым наиболее чувствительны
эксплуатационные коэффициенты —
коэффициент технического использования
(24), коэффициент готовности (28), коэффициент
неработоспособности локомотивов (26).
Показателями чувствительности
являются значения частных производных
от эксплуатационных коэффициентов по
каждому из параметров ![]() процесса
функционирования локомотива.
процесса
функционирования локомотива.
С
помощью эксплуатационных коэффициентов
можно оценить эффективность различных
организационно-технических мероприятий,
направленных на повышение надежности
локомотивов. Если в результате проведения
какого-либо мероприятия увеличиваются
средние значения наработки ![]() до
отказа первого и второго типа,
увеличивается наработка до планового
ремонта
до
отказа первого и второго типа,
увеличивается наработка до планового
ремонта ![]() или
сокращается время простоя локомотива
на внеплановом ремонте
или
сокращается время простоя локомотива
на внеплановом ремонте ![]() или на плановом ремонте T8
и т.д., то в результате коэффициенты
технического использования Kи
и готовности Kr
увеличиваются, а коэффициент
неработоспособности Kн
— уменьшается, что приводит к общему
улучшению всех технико-экономических
показателей работы локомотивного
парка.
или на плановом ремонте T8
и т.д., то в результате коэффициенты
технического использования Kи
и готовности Kr
увеличиваются, а коэффициент
неработоспособности Kн
— уменьшается, что приводит к общему
улучшению всех технико-экономических
показателей работы локомотивного
парка.
Методы расчета эксплуатационных коэффициентов иллюстрируются решением следующих задач.
Задача
Упрощенная модель функционирования электровоза задана графом, показанным на рис. 9.
Состояния электровоза:
Электровоз исправен и работает.
Восстанавливается в пути следования.
Находится на внеплановом ремонте.
Находится на плановом ремонте.
Определить коэффициент готовности электровоза.
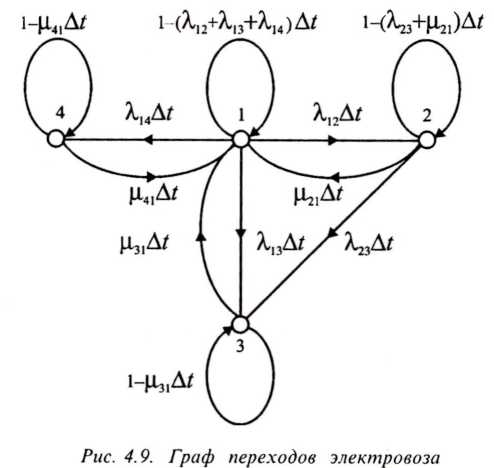
Рисунок 9– Граф переходов электролиза
Уравнения Колмогорова записываются в следующем виде:
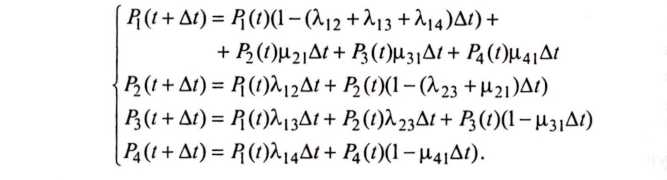
Выполнив соответствующие преобразования, получим следующую систему дифференциальных уравнений:
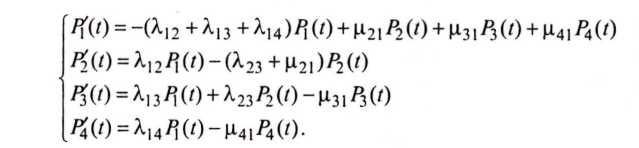
Поскольку
граф переходов, показанный на рис. 9,
является связным, то процесс
функционирования электровоза имеет
установившимся режим, в котором
вероятности состоянии перестают
зависеть от времени и принимают финальные
значения ![]() ,
а их производные равны 0. В установившемся
режиме система дифференциальных
уравнений преобразуется в систему
алгебраических уравнений:
,
а их производные равны 0. В установившемся
режиме система дифференциальных
уравнений преобразуется в систему
алгебраических уравнений:

Из второго уравнения выражаем
![]()
Из третьего уравнения выражаем
![]() Из
четвертого уравнения выражаем
Из
четвертого уравнения выражаем
![]()
Выражения
всех вероятностей подставляем в
уравнение ![]() получаем
получаем
![]()
Поскольку электровоз работоспособен, только находясь в первом состоянии, коэффициент готовности Кr= Р1.
Из
уравнений 2, 3 и 4 выражаем вероятности
![]() через вероятность
через вероятность ![]()
Подставив
эти вероятности в уравнение ![]()
Рассматриваемое устройство работоспособно, только находясь в 0-м состоянии, поэтому вероятность работоспособного состояния при длительной эксплуатации, т.е. коэффициент готовности, равна Кr= Р0.
Обобщив
полученный результат, увидим, что если
устройство имеет отказы п
видов и все ![]() ,
то
,
то
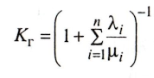
Показатели
безотказности ![]() -
и ремонтопригодности
-
и ремонтопригодности ![]() -
определяются по статистическим
данным в процессе эксплуатации
рассматриваемого устройства.
-
определяются по статистическим
данным в процессе эксплуатации
рассматриваемого устройства.
