2. Надежность объектов с двумя возможными состояниями — схема «отказ-—восстановление»

Рассмотрим технический объект, который функционирует сле­дующим образом: объект работает непрерывно до отказа, после которого немедленно начинается восстановление его работоспо­собного состояния, после восстановления объект сразу вступает в работу и работает непрерывно до следующего отказа и т.д.

Рисунок 4 - Временная диаграмма

Временная диаграмма функционирования объекта представлена на рис. 4.

Здесь:

τ_i — время безотказной работы до i-го отказа;

τ_bi— время восстановления работоспособности после i-го отказа.

В процессе функционирования объект может находиться в произвольно взятый момент времени в одном из двух состояний.

1. Объект работоспособен, выполняет свои функции.

2. Объект неработоспособен, восстанавливается после отказа.

Предположим, что время безотказной работы и время восста­новления работоспособности являются экспоненциально распре­деленными случайными величинами. При этом допущении про­цесс функционирования рассматриваемого объекта является мар­ковским. Обозначим:

F (t) — функция распределения времени безотказной работы

г де λ— интенсивность отказов (или параметр потока отказов со, так как для простейшего потока отказов λ = ω),

где Т₀ — среднее время безотказной работы.

F_B(t)— функция распределения времени восстановления рабо­тоспособности

г де — интенсивность восстановления,

где —среднее время восстановления.

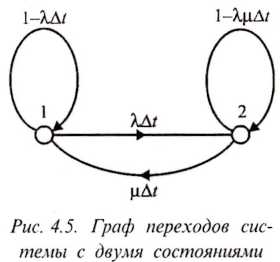При отказе объекта он переходит из 1-го состояния во 2-е, а при восстановлении работоспособности — из 2-го в 1-е.

Для решения этой системы необходимо задать начальные ус­ловия. Здесь их может быть два:

Вероятности переходов за бесконеч­но малый промежуток времени Δt в со­ответствии с (7) определяются в виде:

Рисунок 5- Граф переходов системы с двумя состояниями

Если за время Δt не происходит отказ объекта, то он остается в 1-м состоянии с вероятностью 1 - ; если за время Δt работоспособность отказавшего объекта не будет восстановлена, то он остается во 2-м состоянии с вероятностью 1 –

Граф переходов рассматриваемого объекта показан на рис. 5.

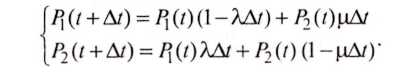В соответствии с рекуррентной формулой (9) запишем урав­нения Колмогорова, связывающие между собой вероятности

Раскрыв скобки, перенеся в i-м уравнении (i = 1—2) из пра­вой части в левую и разделив обе части равенств на Δt, получим

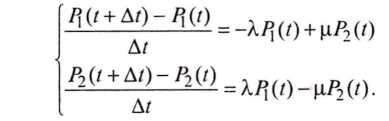
Перейдем к пределу при Δt→0, и, учитывая то, что

получим систему дифференциальных уравнений:

(11)

Для решения этой системы необходимо задать начальные ус­ловия. Здесь их может быть два:

а) , , если в начальный момент времени объект находится в работоспособном состоянии;

б) , , если в начальный момент времени объект восстанавливается.

С

(12)

истему дифференциальных уравнений проще всего решить опера­торным методом. Обозначим преобразование Лапласа символом L:

т.е. преобразование Лапласа L переводит функцию P(t) в изоб­ражение P(s), а производную P'{t) в ее изображение sP{s) - Р(0). Здесь s — оператор Лапласа; Р(0)— начальное условие .

Применив преобразование Лапласа (12) к системе дифферен­циальных уравнений (11) при начальных условиях а, получим следующую систему алгебраических уравнений:

(13)

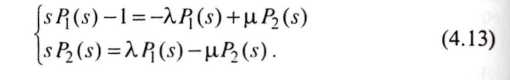
(14)

Решив систему уравнений (13), получим изображение Pi(s), оно равно:

Для того чтобы привести выражение P_i(s) к табличному, умно­жим и разделим правую часть на величину, равную (λ+μ). В ре­зультате получим:

По таблице обратного преобразования Лапласа находим

Так как в любой момент времени система находится либо в 1-м, либо во 2-м состоянии, то

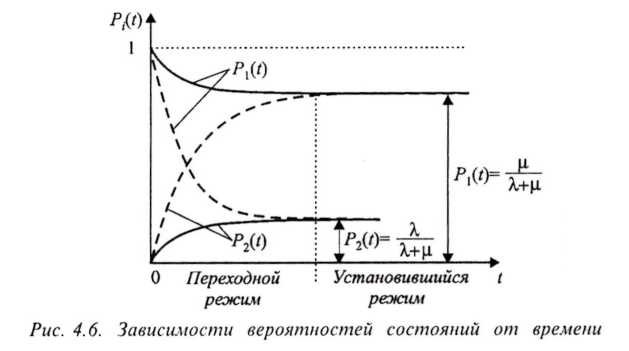
Рисунок 6 - Зависимости вероятностей состояний от времени состояниями

Подставив в (15) выражение (14), получим

(16)

Графики функций P₁(t) и Р₂(t) показаны на рис. 6 сплошны­ми линиями

Решив систему дифференциальных уравнений (11) при началь­ных условиях б, получим следующие выражения вероятностей состояний рассматриваемого объекта:

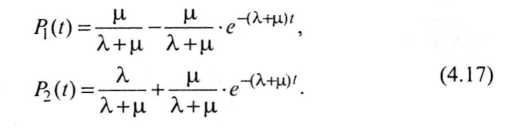
(17)

Н

(17)

а рис. 6 зависимости P₁(t) и P₂(t), определяемые выраже­ниями (17), показаны штриховыми линиями.

Из выражений (14), (16) и (17), а также из графиков (см. рис. 6) видно, что у процесса функционирования рассматрива­емого объекта существует установившийся режим, в котором ве­роятности состояний перестают зависеть от времени и независи­мо от начальных условий принимают установившиеся (финаль­ные) значения Р₁ и Р₂.

Вероятности (18)

т. е. они характеризуют надежность объекта при его длительной эксплуатации.

Р₁ — вероятность того, что объект окажется в работоспособ­ном состоянии в произвольно взятый момент времени t, доста­точно удаленный от начала эксплуатации,

Р₂ — вероятность того, что в произвольный достаточно уда­ленный от начала эксплуатации момент времени t объект ока­жется неработоспособным.

Нельзя путать вероятности Р₁ и Р₂, с вероятностью безотказ­ной работы и вероятностью отказа, так как последние характе­ризуют непрерывный режим эксплуатации объекта. Вероятнос­ти Р₁ и Р₂ формируются в результате неоднократного прерыва­ния процесса эксплуатации, смены работоспособного и нерабо­тоспособного состояний.

Установившиеся значения вероятностей Р₁ и Р₂ можно опре­делить, не решая систему дифференциальных уравнений (11) .

Поскольку в установившемся режиме Р₁ = const и Р₂ = const, то и , а система (4.11) превращается в систему

(19)

Решив систему уравнений (19) при условии Р₁+Р₂= 1, по­лучим выражения финальных вероятностей Р₁ и Р₂.

(20)

Выразив в (20) интенсивности μ и λ через среднее время получим

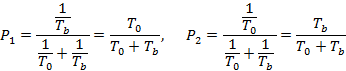
Сумма Т₀ + Т_в определяет среднюю продолжительность одно­го цикла «безотказная работа — восстановление» процесса фун­кционирования, который у рассматриваемого объекта заключа­ется в постоянном повторении этого цикла (рис. 7).

Отношение показывает, какую долю в средней продолжительности одного цикла занимает среднее время, в течение которого объект находится в работоспособном состоянии, т.е. готов выполнять свои функции. Поэтому вероятность Р₁ назы­вается коэффициентом готовности

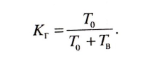
(21) Если, например, К_r= 0,8, то это означает, что в среднем 80 % времени рассматриваемый объект находится в работоспособном состоянии и готов выполнять свои функции.

Поскольку марковские процессы обладают эргодичностью , в соответствии с которой среднее по времени равно среднему по ансамблю, при ЛГ_г = 0,8 из каждых 10 объектов в любой произ­вольно взятый момент времени, достаточно удаленный от начала эксплуатации, в среднем 8 объектов находятся в работоспособном со­стоянии, а 2 объекта восстанавли­ваются после отказа.

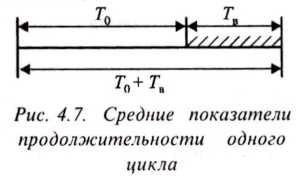
Рисунок 7- Средние показатели продолжительности одного цикла

Из рассмотренного примера ана­лиза надежности объектов с двумя возможными состояниями можно сформулировать следующий ал­горитм решения задач на основе теории марковских процессов.

1. На основе анализа процесса функционирования выделяют­ся характерные состояния, в которых может находиться рассмат­риваемый объект.

2. Разрабатывается математическая модель функционирования рассматриваемого объекта в виде графа переходов или матрицы вероятностей переходов.

3. Записывается система уравнений Колмогорова, связываю­щая между собой вероятности нахождения объекта в каждом из состояний в соседние моменты времени t и t + Δt.

4. Полученная система конечно-разностных уравнений преоб­разуется в систему дифференциальных уравнений, решение кото­рой при заданных начальных условиях, дает зависимости Pi(t) для всех п рассматриваемых состояний объекта.

5. Если граф переходов рассматриваемого объекта является связным, т.е. объект из любого состояния может перейти в лю­бое другое состояние за конечное число шагов, то процесс его функционирования имеет установившийся режим, в котором ве­роятности всех состояний перестают зависеть от времени, прини­мая финальные значения

6.В установившемся режиме система дифференциальных уравнений преобразуется в систему алгебраических уравнений,

так как

Решение полученной системы алгебраических уравнений при условии

Дает значения финальных вероятностей Р_i , i = 1, 2, ..., п.