Кафедра электротехники и электрических машин

Лекция № 4

по дисциплине «Надежность электрооборудования предприятий и учреждений»

для студентов направления подготовки:

13.03.02 «Электроэнергетика и электротехника»

Тема № 4. Комплексные показатели надежности

Краснодар 2015 г.

Цели: 1. Формирование следующих компетенций:

1. ПК-7. Готовность обеспечивать требуемые режимы и заданные параметры технологического процесса по заданной методике.

2. ПКд-2. Способность проводить экспериментальные исследования в профессиональной области и обрабатывать результаты экспериментов.

2. Формирование уровня обученности:

должны знать основы методов обеспечения требуемых режимов и заданных параметров технологического процесса по заданной методике.

Материальное обеспечение:

Проектор, ПК.

Учебные вопросы

Вводная часть.

Основная часть:

1. Основы теории марковских процессов

2. Надежность объектов с двумя возможными состояниями – схема "отказ – восстановление".

Заключение.

Литература

1. Шишмарев, В.Ю. Надежность технических систем [Текст]: учеб. для вузов / В.Ю. Шишмарев. – М.: Академия, 2010. – 304 с. 2. Александровская, Л.Н. Современные методы обеспечения безотказности сложных технических систем: Учебник / Л.Н. Александровская, А.П. Афанасьев, А.А. Лисов. – М.: Логос, 2013. – 208 с.

1. Основы теории марковских процессов

Кроме показателей, которые характеризуют одно из свойств, определяющих надежность технического объекта, безотказность, ремонтопригодность, сохраняемость или долговечность, суще­ствуют показатели, которые характеризуют сразу несколько из этих свойств, например безотказность и ремонтопригодность.

П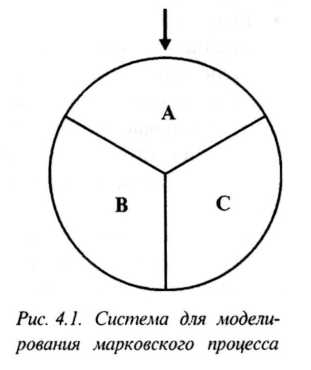 ри определении комплексных показателей рассматривается не одно состояние объекта, например работоспособное или неработоспособное, а анализируется процесс перехода объек­та из одного состояния в другое, причем процесс этот — случай­ный, т.е. переходы осуществляются с определенными вероятнос­тями. Математическим аппаратом для описания функционирова­ния таких объектов является теория марковских процессов .

Марковским называется такой процесс перехода объекта или системы из одного состояния в другое, в котором вероятности перехода зависят от того, между какими состояниями осуще­ствляется переход, и не зависят от того, каким образом рассматрива­емая система попала в то состоя­ние, из которого осуществляется переход. Последнее свойство на­зывается отсутствием последей­ствия, или отсутствием «памяти» у рассматриваемого процесса.

А

Рисунок 1 – Система для моделирования марковского прцесса

лгоритм анализа марковского процесса рассмотрим на примере системы (рис. 1), состоящей из диска, разделенного на три сектора А, В и С, и стрелки-указателя.

Рассматриваемая система может находиться в трех состояниях:

• Напротив указателя расположен сектор А.

• Напротив указателя расположен сектор В.

• Напротив указателя расположен сектор С.

Переход (перевод) системы из одного состояния в другое осу­ществляется с помощью следующего вероятностного механизма:

• если система находится в состоянии 1, то состояние, в кото­рое она перейдет, определяется путем бросания монеты.

Если монета выпадает вверх гербом, то система переходит в

состояние 2 (под указатель переводится сектор В), если же моне­та выпадает вверх цифрой — то в состояние 3.

Обозначим Pij — вероятность перехода из состояния с номе­ром j в состояние с номером j.

Очевидно, что в рассматриваемой ситуации Р11 =0, P₁₂ = 0,5, P₁₃ = 0,5.

• Если система находится в состоянии 2, то состояние, в которое она будет переведена, определяется путем бросания игральной кости. Если выпадает нечетное число 1, 3 или 5, то система перехо­дит в состояние 1; если выпадает цифра 2, то система остается во 2-м состоянии; если выпадают цифры 4 или 6, то система пере­ходит в состояние 3.

В этой ситуации вероятности переходов равны следующим ве­личинам: Р₂₁ = 0,5, Р₂₂ = 1/6, P₂₃ ⁼ 1/3.Если система находится в состоянии 3, то следующее состоя­ние определяется путем бросания 2 монет.

Если одна монета выпадает вверх гербом, а другая цифрой (такому исходу испытаний благоприятствуют 2 варианта: 1-я монета выпадает гербом, 2-я цифрой; и наоборот), то система пе­реходит в состояние 1; если обе монеты выпадают вверх гербом, то система переходит в состояние 2; если обе монеты выпадают вверх цифрой, то система находится (остается) в состоянии 3. Несложно подсчитать, что Р₂₁=0,5, P₃₂ = 0,25, P₃₃ = 0,25. Вероятности переходов системы из одного состояния в дру­гое удобно представлять в виде квадратной матрицы, в которой число строк и столбцов равно числу состояний системы, номера строк — номера состояний, из которых система «уходит», а но­мера столбцов — в которые она переходит, на пересечении i-й строки и j-го столбца записывается вероятность Рij. В рассматриваемом примере матрица вероятностей переходов имеет вид:

Сумма вероятностей, стоящих в одной строке, равна 1, т.е.

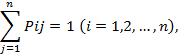
где п — число состояний системы.

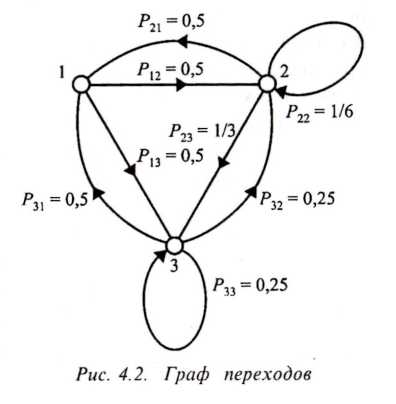Более наглядный вид имеет представление марковского процес­са в виде графа переходов, в котором вершины — это состояния си­стемы, стрелки — направления переходов, а около каждой стрелки указывается вероятность соответствующего перехода (рис. 2).

Для рассматриваемого примера граф переходов выглядит сле­дующим образом.

Задания марковского процесса в виде матрицы вероятностей переходов или в виде графа переходов являются равносильны­ми, т.е. если задана матрица, то по ней легко построить граф переходов и, наоборот.

Для того чтобы марковс­кий процесс был полностью определен, кроме матрицы вероятностей (графа) пере­ходов, необходимо задать начальное условие, т.е. ука­зать вероятности, с которы­ми рассматриваемая систе­ма находилась в каждом из состояний на

н

Рисунок 2 – Граф переходов

улевом шаге процесса, где под шагом понимается один переход системы из состояния i в состояние j, в том числе и в случае, когда i - j.

Обычно на нулевом шаге фиксируется одно из состояний, т. е. его вероятность считается равной 1, а вероятности всех осталь­ных состояний равны 0.

Обозначим Рi(к) — вероятность того, что рассматриваемая система находится в состоянии i на к-м шаге процесса.

Начальные условия задаются в виде вектора-строки, компо­нентами которого являются вероятности Pi(0), i = 1, 2, п.

Для рассматриваемого примера начальные условия задаются следующим образом:

а) — система находится в состоянии 1.

б) — система находится в состоянии 2.

в) —система находится в состоянии 3.

Если известны матрица вероятностей или граф переходов и за­дан вектор распределения вероятностей (начальные усло­вия), то можно рассчитать вероятности, с которыми система бу­дет находиться в одном из состояний на любом шаге процесса.

Для рассматриваемого примера выберем начальные условия а), т.е. и рассчитаем Pj(k) для i = 1,2, 3 и к - 1,2, 3,4,..., п.

Система окажется в состоянии 1 на первом шаге процесса (к = 1), если она находилась в этом состоянии на нулевом шаге и осталась в нем, или она находилась во 2-м состоянии на нуле­вом шаге и перешла из 2-го состояния в первое, или она нахо­дилась в 3-м состоянии и перешла из него в 1-е состояние.

Вероятность того, что система будет находиться в 1 -м состоя­нии на 1-м шаге процесса, находится как вероятность сложного события по теоремам умножения и сложения вероятностей:

Аналогично находятся вероятности того, что на 1-м шаге сис­тема будет находиться во 2-м или 3-м состоянии:

Распределение вероятностей состояний системы на первом шаге процесса {к = 1) представим в виде вектора-строки: Р(1) = (0; 0,5; 0,5).

Зная распределения вероятностей состояний системы на первом шаге, можно рассчитать вероятности состояний на 2-м шаге, а зная их, можно рассчитать вероятности состоя­ний на 3-м шаге и т.д.

Вероятности состояний системы на 2-м шаге:

Далее аналогично:

Зависимости вероятностей состояний системы от номера шага процесса переходов Рi(к), i = 1, 2, 3 показаны на рис. 3.

И

3

з рис. 3 видно, что вероятности каждого из состояний после 6—7-го шага практически перестают изменяться, принима­ют так называемые установившиеся или финальные значения, т.е. наступает установившийся режим функционирования системы.

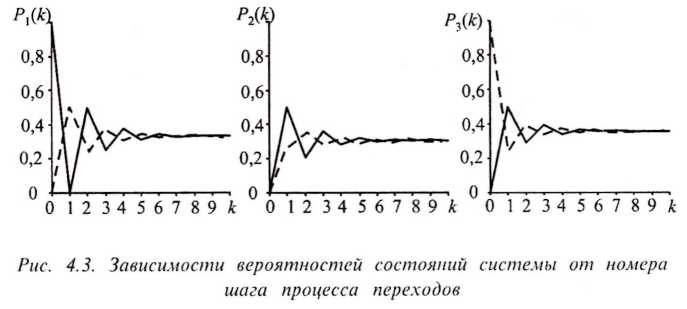
Рисунок 3 – Зависимость вероятностей состояний системы от номера шага процесса переходов

Установившийся режим существует только у таких систем, у кото­рых граф переходов является связным, т.е. из любого состояния систе­ма может перейти в любое другое состояние за конечное число шагов.

Граф переходов рассматриваемой системы является связным (см. рис.2), так как все переходы из одного состояния в другое осу­ществляются за один шаг, кроме перехода из первого состояния в первое. Этот переход осуществляется за два шага, например систе­ма из первого состояния переходит во второе, а из него в первое.

Если задаться другими начальными условиями, например , то, проделав аналогичные выкладки, получаем зависимости вероятностей состояний от номера шага процесса переходов, показанные на рис. 3 штриховыми линиями.

Из рис. 3 видно, что независимо от начальных условий финаль­ные значения вероятностей каждого из состояний принимают одну и ту же величину

Р_i (к) = const = P_i, где P_i — финальное значение вероятности i-го состояния не

к→∞ зависящее от номера перехода к.

Финальные значения вероятностей для разных состояний раз­личные Р_1≠ Р₂≠ Р₃ причем Р₁ + Р₂ + Р₃ = 1.

В общем виде для системы, имеющей п различных состояний, сумма финальных вероятностей всех состояний равна 1:

(1)

Алгоритм расчета вероятностей состояний системы можно представить в виде следующей рекуррентной формулы:

(2)

где Pj(k + 1) — вероятность того, что система будет находиться в j-м со­стоянии (j= 1,2, ...,n) на (к + 1)-м шаге процесса переходов;

Pj(k) — вероятность того, что система находится в /-м состоянии

(j=1,2,..., п) на к-м шаге;

Pij—вероятность перехода из i-го состояния j-е;

п — число различных состояний системы.

Формула (2) носит название уравнения Маркова в честь россий­ского ученого А. А. Маркова (1856—1922), который впервые разра­ботал математический аппарат исследования особого вида случай­ных процессов, которые впоследствии были названы марковскими.

В рассматриваемом примере вероятности переходов Рij- явля­лись постоянными величинами. На практике обычно эти веро­ятности зависят от времени , в течение которого система нахо­дилась в г-м состоянии до перехода в j-е состояние.

Допустим, т ij—случайная величина, которая для любых ком­бинаций i, j описывается экспоненциальным законом с функци­ей распределения

(3)

Здесь λ_ij— интенсивность переходов системы из i-го в j-е состояние:

(4)

где Tij — среднее время пребывания системы в м состоянии до перехо­да в j-е состояние.

При сделанных допущениях процесс переходов системы из одного состояния в другое будет марковским, так как экспоненциальный за­кон имеет свойство отсутствия последействия (отсутствие «памяти»), что является характеристическим признаком марковского процесса.

Рассмотрим процесс перехода системы из одного состояния в другое за бесконечно малый промежуток времени Δt.

По определению т.е. функция распределе­ния равна вероятности того, что за время Δt будет осуществлен переход из i-го в j-е состояние:

(5)

В силу ординарности экспоненциального закона распределе­ния система, перейдя из i-го состояния в j-е, не успеет перейти в какое-либо другое состояние за время Δt.

Разложим в выражении (5) функцию в ряд Тейлора

(6)

В нашем случае

Следовательно

Подставляя полученные значения в (6), получаем:

В этом выражении все члены, начиная с

я вляются ве­личинами высшего порядка малости по сравнению с At, поэто­му ими можно пренебречь, отсюда

П

(7)

одставляя это выражение в (5), получаем, что вероятность перехода системы из состояния i в состояние j за бесконечно малый промежуток времени Δt равна:

Матрица вероятностей переходов в этом случае имеет вид:

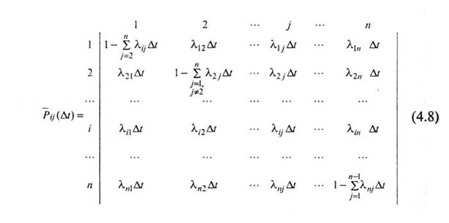
(8)

В

(9)

случае, когда вероятности переходов являются функциями времени, вероятности состояний тоже являются функциями вре­мени, и уравнение (2) принимает следующий вид:

(9)

где Pj(t) — вероятность того, что рассматриваемая система находится в /-м состоянии в момент времени /;

Pj(t + Δt) — вероятность пребывания системы в j-м состоянии в мо­мент времени I + Д/;

Pjj(Δt) — вероятность перехода системы из i-го в у'-е состояние за вре­мя Δt

п — число состояний системы.

Выражение (4.9) носит название уравнения Колмогорова, в честь советского математика А.Н. Колмогорова (1903—1987), впервые разработавшего математический аппарат исследования марковских процессов, в которых вероятности состояний и пе­реходов являются функциями времени.

Д

(10)

ля того чтобы марковский процесс, зависящий от времени, был полностью определен, необходимо кроме матрицы вероят­ностей переходов задать —начальное распределение веро­ятностей состояний в момент времени t= 0.

Имея распределение (10) и матрицу (8), с помощью урав­нения Колмогорова (9) можно рассчитать вероятности Pi(t), с которыми рассматриваемая система будет находиться в i-м со­стоянии i= 1,2, ...,n в произвольный момент времени t.