
Плоскость в пространстве
Составим уравнение плоскости,
проходящей через данную точку
![]() перпендикулярно данному вектору
перпендикулярно данному вектору
![]() .
Пусть
.
Пусть
![]() - произвольная точка плоскости. То, что
M
принадлежит плоскости, означает, что
- произвольная точка плоскости. То, что
M
принадлежит плоскости, означает, что
![]() .
Раскрыв скобки и обозначив
.
Раскрыв скобки и обозначив
![]() ,
получим
,
получим
![]() - общее уравнение плоскости, если
,
или
.
Ненулевой вектор,
перпендикулярный данной плоскости
называется нормальным вектором этой
плоскости.
- общее уравнение плоскости, если
,
или
.
Ненулевой вектор,
перпендикулярный данной плоскости
называется нормальным вектором этой
плоскости.
Составим теперь уравнение плоскости,
проходящей через данную точку
параллельно двум данным векторам
![]() и
и
![]() .
Возьмём
.
Возьмём
![]() ,
принадлежащую нашей плоскости. Это
значит, что
,
принадлежащую нашей плоскости. Это
значит, что
![]() ,
,
![]() и
компланарны, т.е.
и
компланарны, т.е.
 - уравнение плоскости, проходящей через
данную точки параллельно двум данным
векторам.
- уравнение плоскости, проходящей через
данную точки параллельно двум данным
векторам.
Для того чтобы провести плоскость через
три данные точки
![]() ,
,
![]() ,
,
![]() достаточно взять
достаточно взять
![]() и
и
![]() .
Тогда
.
Тогда
 и есть искомое уравнение плоскости.
и есть искомое уравнение плоскости.
Частные случая общего уравнения плоскости
Общее уравнение плоскости
называется полным, если
,
,
и
![]() .
Тогда можно получить уравнение
плоскости в отрезках:
.
Тогда можно получить уравнение
плоскости в отрезках:
![]() ,
где
,
где
![]() ,
,
![]() и
и
![]() .
Здесь a, b
и c – величины отрезков,
отсекаемых плоскостью на осях Ox,
Oy и Oz
соответственно.
.
Здесь a, b
и c – величины отрезков,
отсекаемых плоскостью на осях Ox,
Oy и Oz
соответственно.
Рассмотрим неполные уравнения плоскости:
 - плоскость параллельна оси Ox.
- плоскость параллельна оси Ox. - плоскость параллельна оси Oy.
- плоскость параллельна оси Oy.
 - плоскость параллельна оси Oz.
- плоскость параллельна оси Oz. - плоскость проходит через начало
координат.
- плоскость проходит через начало
координат. - ось Ox принадлежит
плоскости.
- ось Ox принадлежит
плоскости. - ось Oy принадлежит
плоскости.
- ось Oy принадлежит
плоскости. - ось Oz принадлежит
плоскости.
- ось Oz принадлежит
плоскости. - плоскость xOy.
- плоскость xOy. - плоскость yOz.
- плоскость yOz.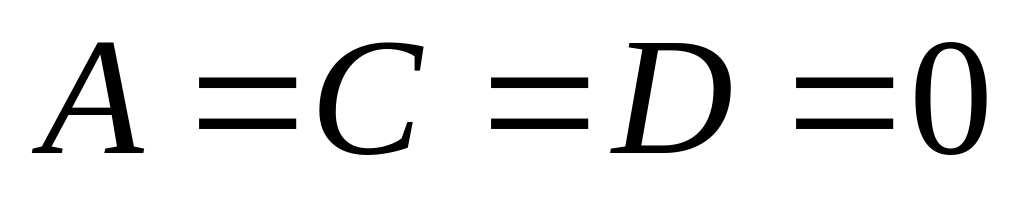 - плоскость xOz.
- плоскость xOz.
Нормальное уравнение плоскости
Уравнение вида
![]() называют нормальным уравнением плоскости,
если
называют нормальным уравнением плоскости,
если
![]() ,
а
,
и
- направляющие косинусы нормального
вектора, направленного из начала
координат в сторону плоскости.
,
а
,
и
- направляющие косинусы нормального
вектора, направленного из начала
координат в сторону плоскости.
Чтобы вычислить расстояние l
от точки
![]() до плоскости, нужно привести уравнение
плоскости к нормальному виду и тогда
до плоскости, нужно привести уравнение
плоскости к нормальному виду и тогда
![]() .
.
Прямая в пространстве
Составим уравнение прямой, проходящей
через точку
параллельно вектору
![]() .
Пусть
принадлежит этой прямой. Это значит,
что
,
т.е.
.
Пусть
принадлежит этой прямой. Это значит,
что
,
т.е.
![]() - канонические уравнения прямой.
- канонические уравнения прямой.
Чтобы составит уравнение прямой,
проходящей через две данные точки
![]() и
,
достаточно взять
и
,
достаточно взять
![]() .
Тогда
.
Тогда
![]() - канонические уравнения этой прямой.
- канонические уравнения этой прямой.
Если взять
![]() ,
то система уравнений
,
то система уравнений
![]() называется параметрическими уравнениями
прямой.
называется параметрическими уравнениями
прямой.
Прямую можно также задать как множество
точек, общих для двух плоскостей системой
уравнений вида
![]() ,
где оба уравнения представляют собой
уравнения пересекающихся плоскостей.
Чтобы перейти от этого вида к каноническому,
достаточно найти одну точку, удовлетворяющую
этому неравенству и взять её как точку
и положить
,
где оба уравнения представляют собой
уравнения пересекающихся плоскостей.
Чтобы перейти от этого вида к каноническому,
достаточно найти одну точку, удовлетворяющую
этому неравенству и взять её как точку
и положить
![]() .
.
Ненулевой вектор, параллельный данной прямой, называется направляющим вектором этой прямой.
Расстояние между двумя скрещивающимися прямыми
П усть
усть
![]() и
и
![]() - уравнения прямых
- уравнения прямых
![]() и
и
![]() .
Тогда
.
Тогда
![]() и
и
![]() - направляющие векторы этих прямых.
Поместим
- направляющие векторы этих прямых.
Поместим
![]() на прямую
на прямую
![]() ,
а начало
,
а начало
![]() совместим с началом
совместим с началом
![]() .
На трёх векторах
,
.
На трёх векторах
,
![]() и
и
![]() построим параллелепипед. Расстояние
между прямыми будет равно высоте
полученного параллелепипеда:
построим параллелепипед. Расстояние
между прямыми будет равно высоте
полученного параллелепипеда:
 .
.
Пусть даны канонические уравнения двух
прямых
и
.
Если
![]() ,
то
,
то
![]() ,
иначе
и
либо пересекаются, либо скрещиваются.
В этом случае достаточно вычислить
смешанное произведение направляющих
векторов этих прямых и вектора,
соединяющего эти прямые. Если оно не
равно нулю, то прямые скрещивающиеся,
иначе – пересекающиеся.
,
иначе
и
либо пересекаются, либо скрещиваются.
В этом случае достаточно вычислить
смешанное произведение направляющих
векторов этих прямых и вектора,
соединяющего эти прямые. Если оно не
равно нулю, то прямые скрещивающиеся,
иначе – пересекающиеся.
