
Аналитическая геометрия
I семестр
Системы координат
Координатной осью называется прямая, на которой:
Указано положительной направление.
Отмечено начало отсчёта.
З
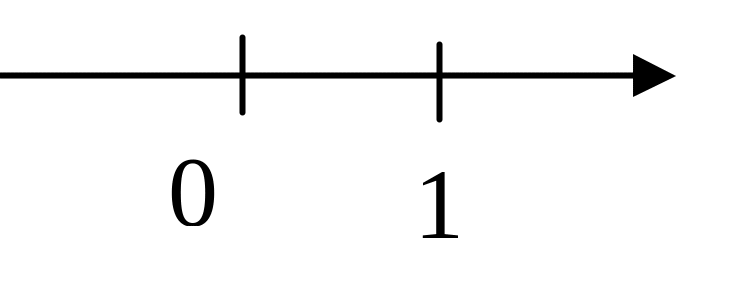 адана
масштабная единица.
адана
масштабная единица.
Направленным отрезком на
прямой называют отрезок, для которого
указано, какая из его граничных точек
является началом и какая – концом.
Обозначение:
![]() .
.
Величиной направленного
отрезка будем называть его длину, взятую
со знаком «+», если отрезок сонаправлен
с координатной прямой и «–» - если нет.
Обозначение:
![]() - величина,
- величина,
![]() - длина.
- длина.
Координатой точки A
на координатной прямой называется
величина отрезка
![]() .
.
Основное тождество: При
любом расположении точек A,
B
и C
справедливо тождество
![]() .
.
П![]() усть,
например, точки расположены так, как
показано на рисунке. Тогда
усть,
например, точки расположены так, как
показано на рисунке. Тогда
![]() ,
,
![]() ,
,
![]()
![]() .
.
Пусть даны
![]() и
и
![]() .
Тогда
.
Тогда
![]() .
.
В силу основного тождества
![]() .
.
Прямоугольная декартова система координат на плоскости
П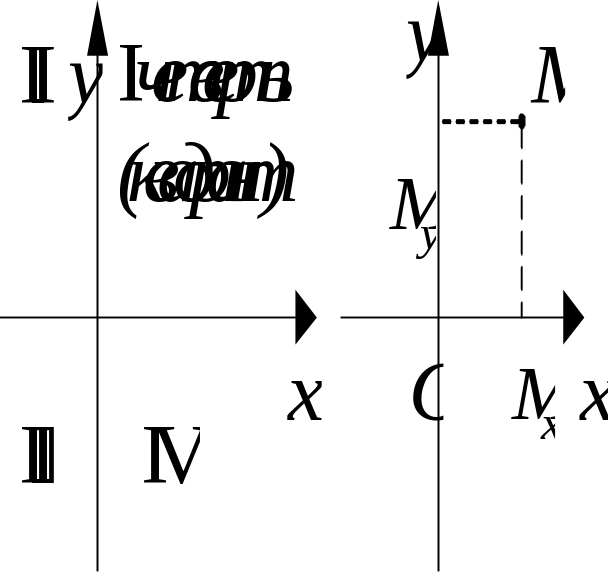 рямоугольной
ДСК на плоскости называют две взаимно
перпендикулярные координатные оси с
общим началом и одинаковой масштабной
единицей. Ox
– ось абсцисс, Oy
– ось ординат.
рямоугольной
ДСК на плоскости называют две взаимно
перпендикулярные координатные оси с
общим началом и одинаковой масштабной
единицей. Ox
– ось абсцисс, Oy
– ось ординат.
Координатой точки на
плоскости называют пару чисел x
и
y,
где
![]()
![]() .
Записываются так:
.
Записываются так:
![]() .
.
Простейшие задачи аналитической геометрии
Пусть даны две точки
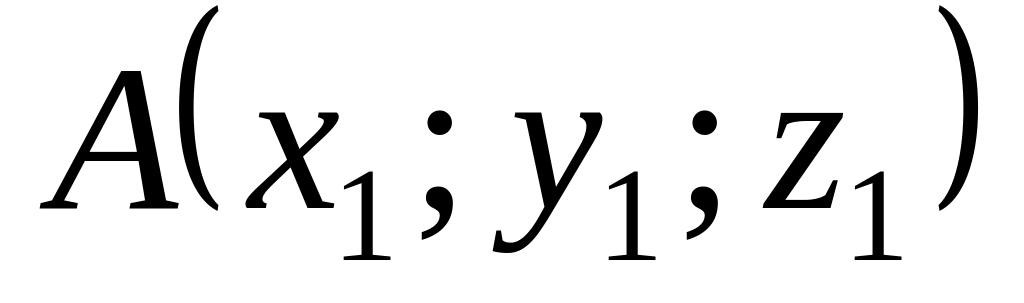 и
и
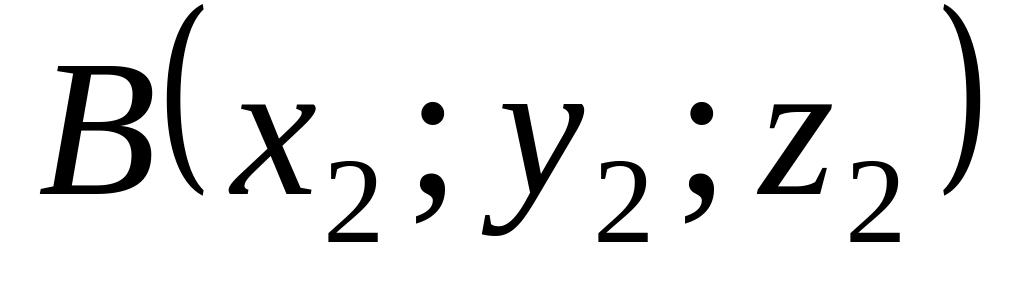 .
Найти расстояние между ними.
.
Найти расстояние между ними.
Согласно теореме Пифагора,
![]() .
.
Деление отрезка в данном отношении.
Говорят, что точка C делит отрезок AB внутренним образом, если C лежит внутри AB и внешним, если C лежит вне AB.
Говорят, что точка C
делит отрезок AB
в отношении ,
если
![]() .
При этом, если
.
При этом, если
![]() ,
то
,
то
![]() ,
иначе
,
иначе
![]() .
.
Замечание:
![]() и
и
![]() .
.
Пусть даны две точки:
и
и пусть C делит AB
в отношении .
Найдём точку C. Пусть
![]() .
Тогда по теореме Фаллеса
.
Тогда по теореме Фаллеса
![]() ,
и
,
и
![]() .
.
Полярная система координат
П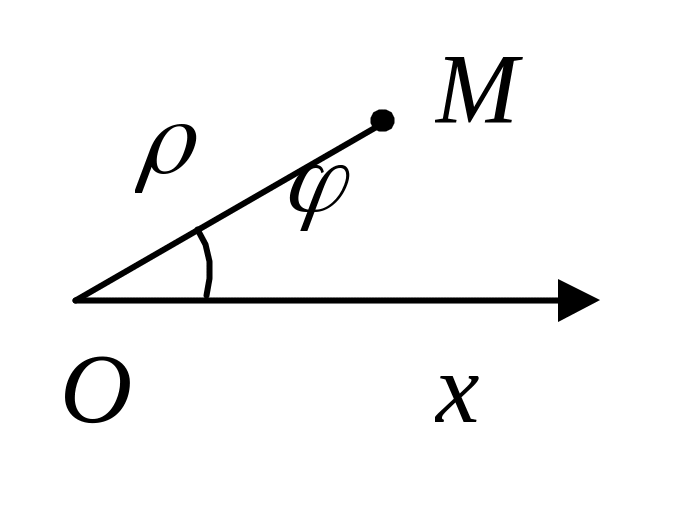 олярной
системой координат называют точку O
(полюс) и луч Ox
(полярная ось), выходящий из этой точки
с масштабной единицей.
олярной
системой координат называют точку O
(полюс) и луч Ox
(полярная ось), выходящий из этой точки
с масштабной единицей.
П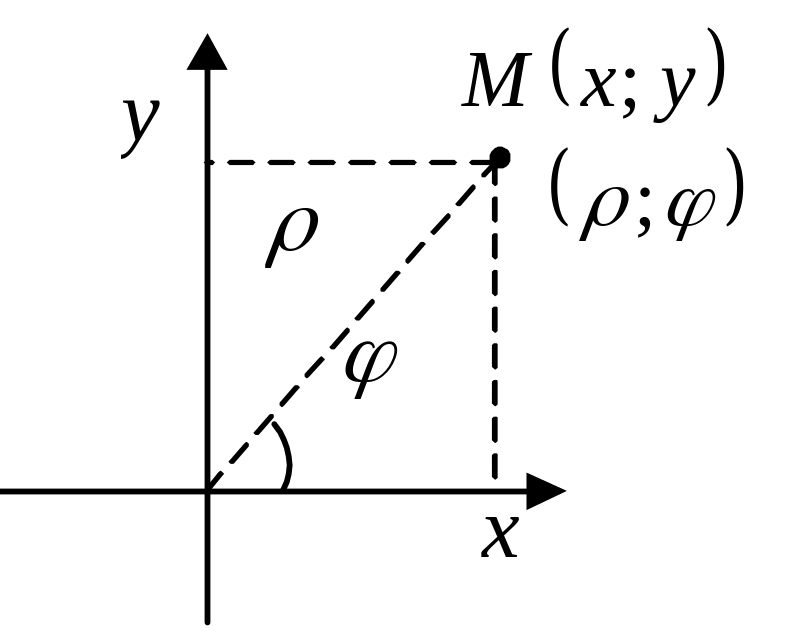 олярными
координатами точки M
называют пару чисел
и ,
где
- расстояние от M
до полюса,
- угол между
радиус-векторами OM
и Ox,
отсчитываемый от полярной оси против
часовой стрелки (
олярными
координатами точки M
называют пару чисел
и ,
где
- расстояние от M
до полюса,
- угол между
радиус-векторами OM
и Ox,
отсчитываемый от полярной оси против
часовой стрелки (![]() ,
,
![]() ).
).
Связь между декартовыми и полярными
координатами:
![]() ,
,
![]() .
.
Векторная алгебра
Основные понятия:
Вектором называют отрезок прямой, если указано, какая из его граничных точек является началом, а какая – концом.
![]() ,
если начало совпадает с концом.
,
если начало совпадает с концом.
Коллинеарными называют
векторы, лежащие на параллельных прямых.
Компланарными – лежащие на одной или
параллельных плоскостях. Равными
называют векторы сонаправленные и
имеющие одинаковую длину. Противоположные
– противоположно направленные и имеющие
одинаковую длину. Ортом
![]() называют единичный вектор, сонаправленный
с
.
называют единичный вектор, сонаправленный
с
.
Линейные операции над векторами:
Сложение векторов выполняется по правилу треугольника или параллелограмма.
Умножение вектора на число.
Произведением вектора
на число
называют вектор
![]() такой,
что
такой,
что ![]() и
и
![]() ,
если
и
,
если
и
![]() ,
если
.
Если
,
если
.
Если
![]() ,
то
,
то
![]() .
У
.
У
![]() произвольное направление.
произвольное направление.
Линейной комбинацией
векторов
![]() называют сумму произведений этих
векторов на произвольные числа:
называют сумму произведений этих
векторов на произвольные числа:
![]() .
.
Если
является линейной комбинацией векторов
,
т.е.
![]() ,
то говорят, что
разложен по векторам
,
а
- разложение.
,
то говорят, что
разложен по векторам
,
а
- разложение.
Базис. Координаты вектора в базисе
Необходимое и достаточное условие
коллинеарности двух векторов: Для
того чтобы
![]() и
и
![]() были коллинеарны, необходимо и достаточно,
чтобы
были коллинеарны, необходимо и достаточно,
чтобы
![]() .
.
Пусть . Тогда, по определению произведения вектора на число,
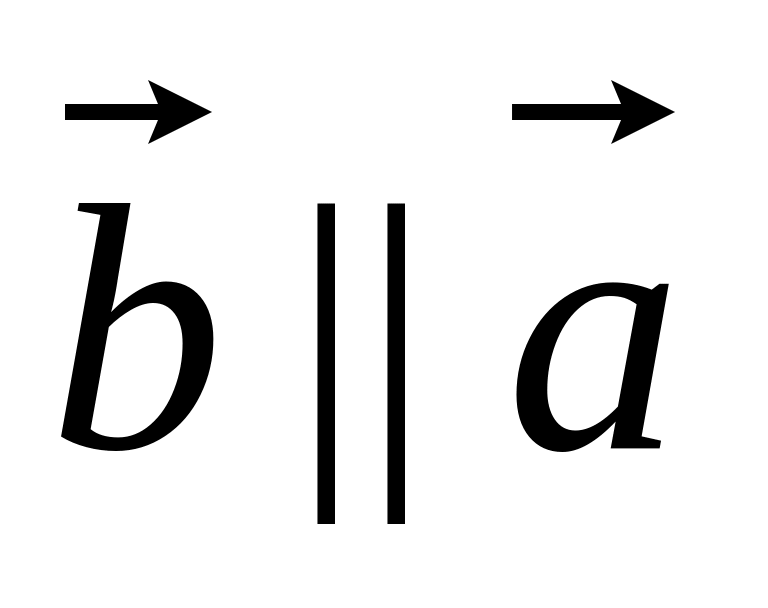 .
.Пусть . Тогда можно взять
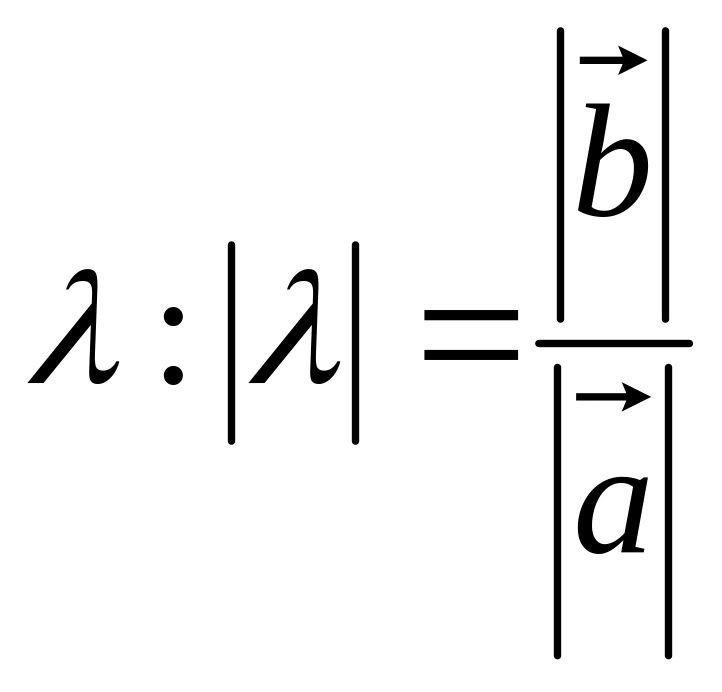 и
,
если
и
,
если
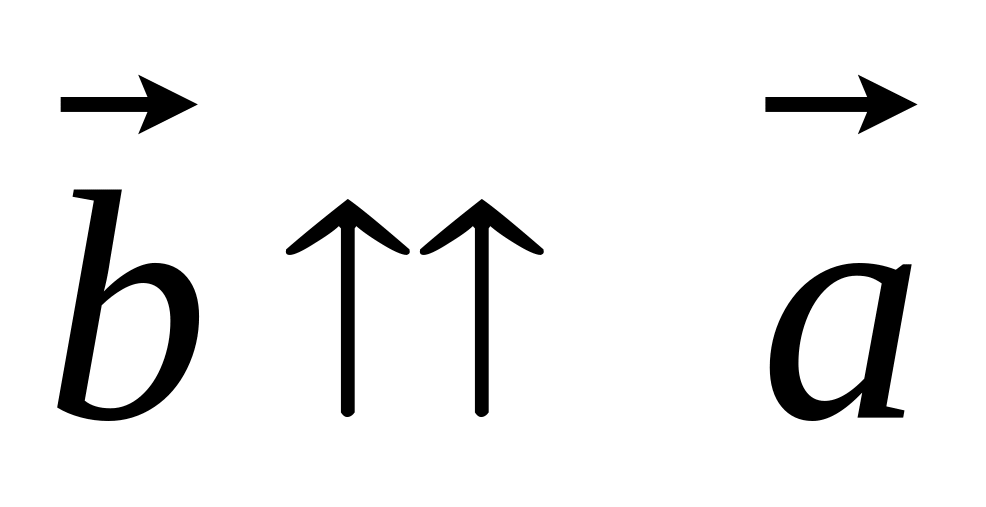 и
,
если
и
,
если  .
Очевидно, что
существует.
.
Очевидно, что
существует.
Л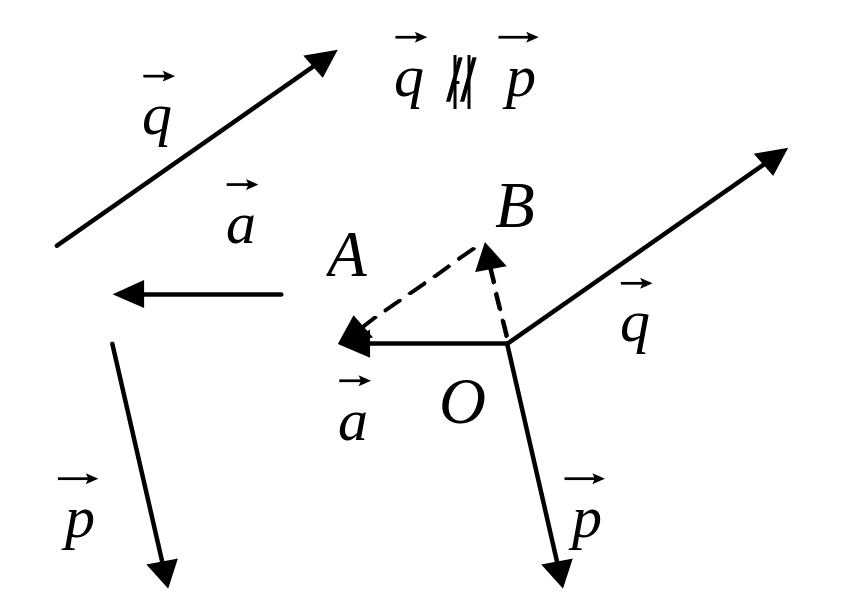 юбой
вектор на плоскости может быть единственным
образом по двум неколлинеарным векторам.
юбой
вектор на плоскости может быть единственным
образом по двум неколлинеарным векторам.
Из рисунка видно, что такое разложение
существует. Докажем единственность.
Действительно,
![]() ,
,
![]() ,
следовательно
,
следовательно
![]()
Пусть также
![]() ,
где
,
где
![]() .
Вычтем из первого уравнения второе.
Получим:
.
Вычтем из первого уравнения второе.
Получим:
![]() .
Т.к.
.
Т.к.
![]() ,
то
,
то
![]() ,
т.е.
,
т.е.
![]() ,
что противоречит условию.
,
что противоречит условию.
Любой вектор в пространстве может быть единственным образом разложен по трём некомпланарным векторам. Доказывается аналогично.
Совокупность векторов, обладающих двумя свойствами: любой вектор может быть выражен через эти вектора и это выражение будет единственным, называется базисом. Таким образом, базис образуют любые два неколлинеарных вектора на плоскости и любые три некомпланарных в пространстве.
Пусть
![]() - базис в пространстве и вектор
- базис в пространстве и вектор
![]() .
Тогда числа ,
и
называют координатами вектора
в базисе
.
.
Тогда числа ,
и
называют координатами вектора
в базисе
.
Базис образует аффинную систему координат.
Углом между векторами
называют наименьший из углов, на который
надо повернуть один вектор до совмещения
с другим по приведения из к общему
началу. Обозначение:
![]() .
.
Орт оси – единичный вектор, сонаправленный с осью.
Углом между вектором и осью называют угол между вектором и ортом оси.
![]()
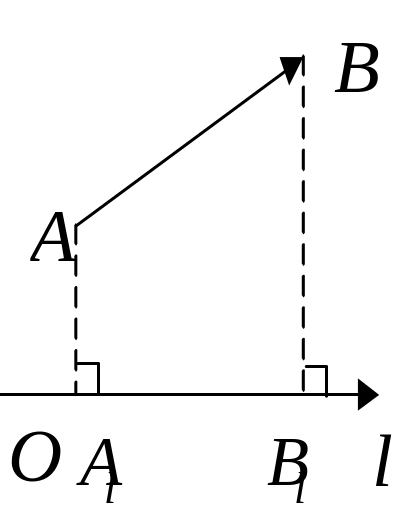 -
геометрическая проекция
-
геометрическая проекция
![]() на ось l.
на ось l.
![]() -
скалярная проекция
на ось l.
-
скалярная проекция
на ось l.
Свойства проекции вектора на ось:
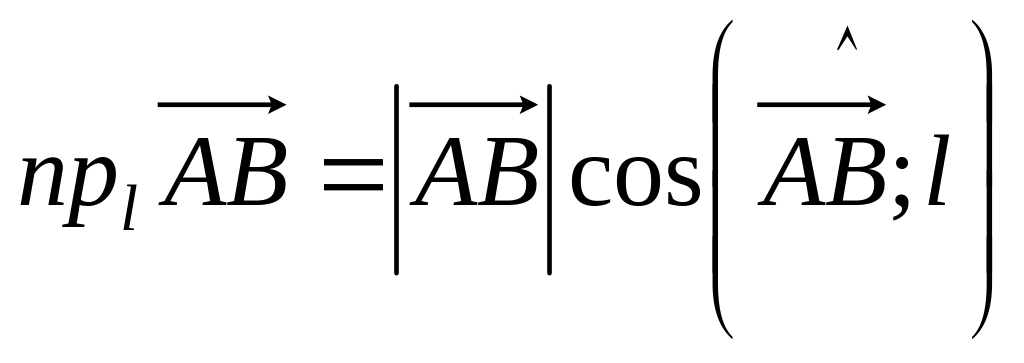 .
.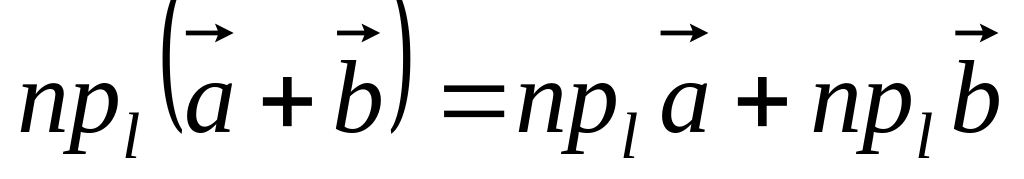 .
.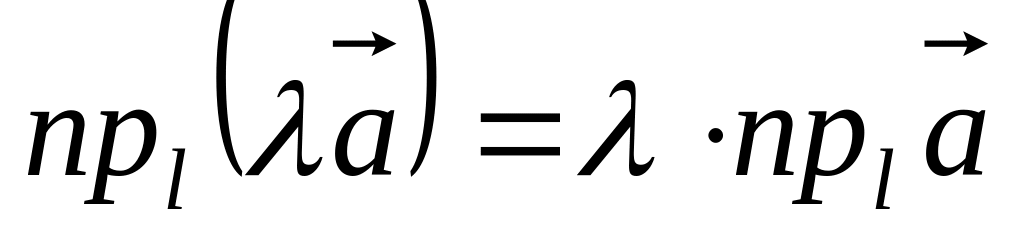 .
.
Координаты вектора в прямоугольной декартовой системе координат
ДСК – частный случай аффинной системы координат.
Разложим
по базису ![]() ,
который образует декартову систему
координат и центр которого совпадает
с началом вектора
:
,
который образует декартову систему
координат и центр которого совпадает
с началом вектора
:
![]() .
Здесь x, y
и z – координаты
вектора в базисе. Тогда
.
Здесь x, y
и z – координаты
вектора в базисе. Тогда
![]() ,
,
![]() ,
,
![]() .
.
Направляющие косинусы вектора в прямоугольной декартовой системе координат
Пусть ,
и
- углы, которые образует
с осями ДСК (Ox,
Oy
и Oz).
Тогда
![]() ,
,
![]() и
и
![]() называют
направляющими косинусами
.
Пусть x, y
и z – координаты
вектора
в ДСК. Тогда
называют
направляющими косинусами
.
Пусть x, y
и z – координаты
вектора
в ДСК. Тогда
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Линейные операции над векторами в аффинных координатах
Пусть
![]() ,
,
![]() .
.
Свойства линейных операций:
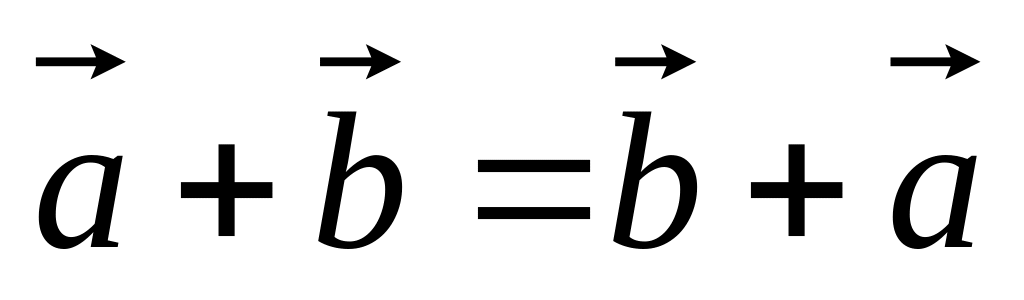 .
.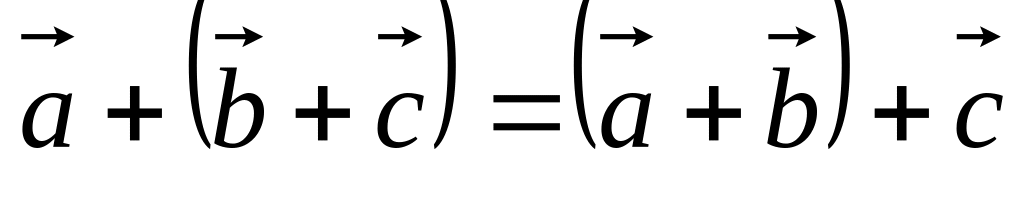 .
.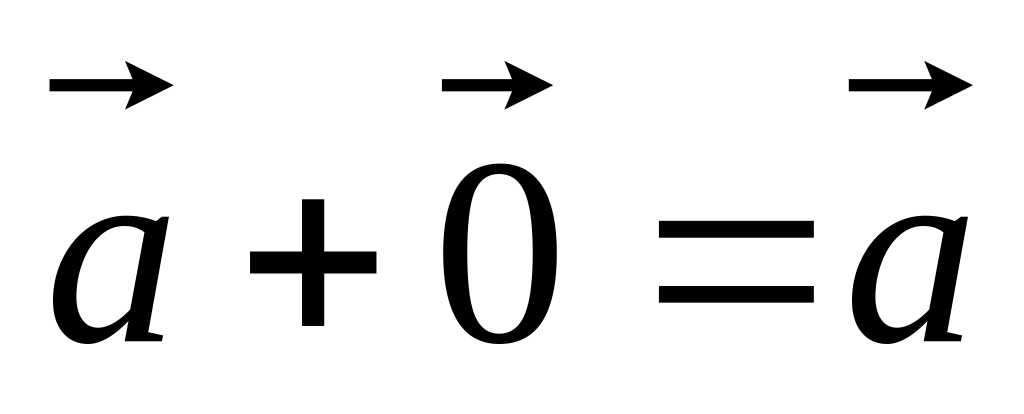 .
.для
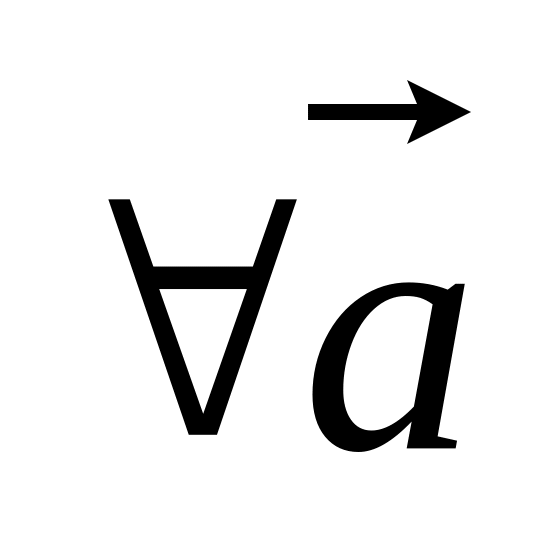
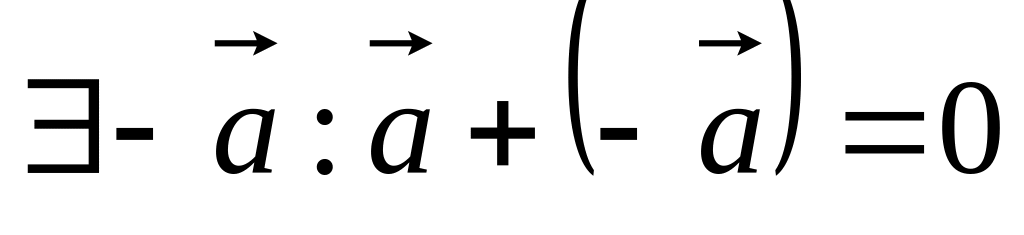 .
.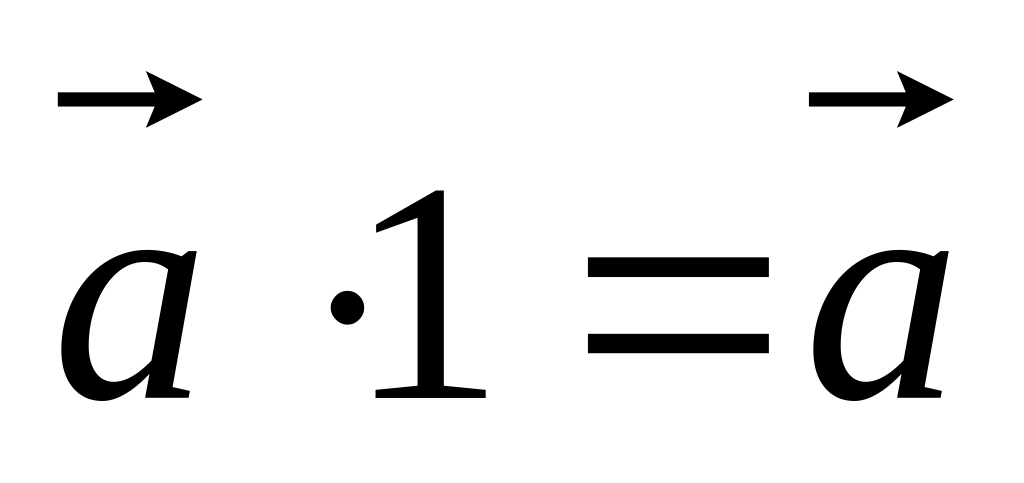 .
.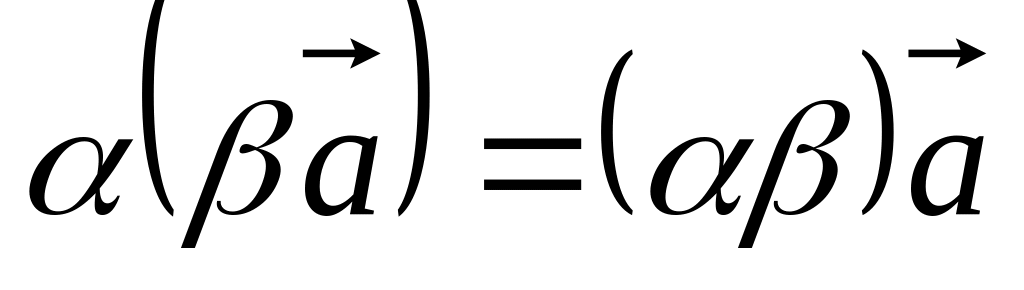 .
.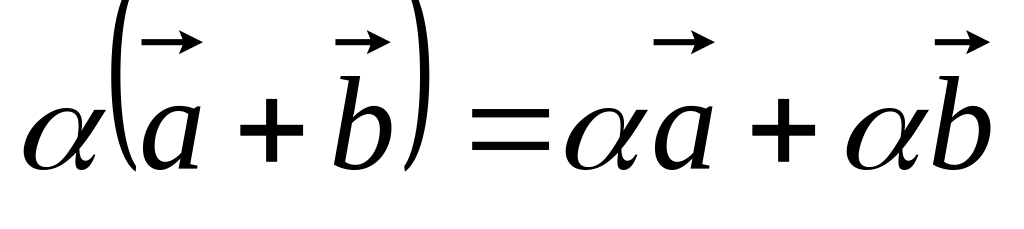 .
.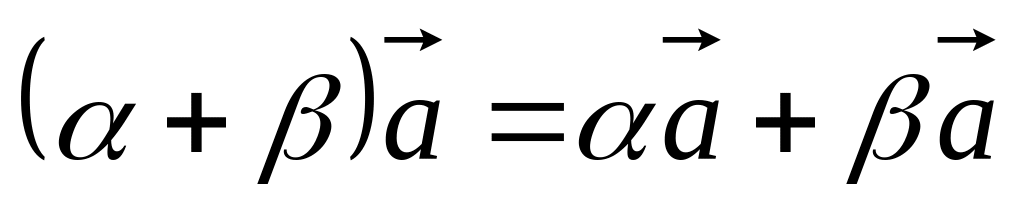 .
.
Пусть в пространстве выбран базис
![]() и пусть
и пусть
![]() и
и
![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Таким образом,
.
Таким образом,
![]() ,
,
![]() .
.
Скалярное произведение
Скалярным произведением
на
называется число
![]() .
.
Второе определение:
![]() .
.
Оба определения равносильны, т.к.
![]() ,
,
![]() .
.
Алгебраические свойства скалярного произведения:
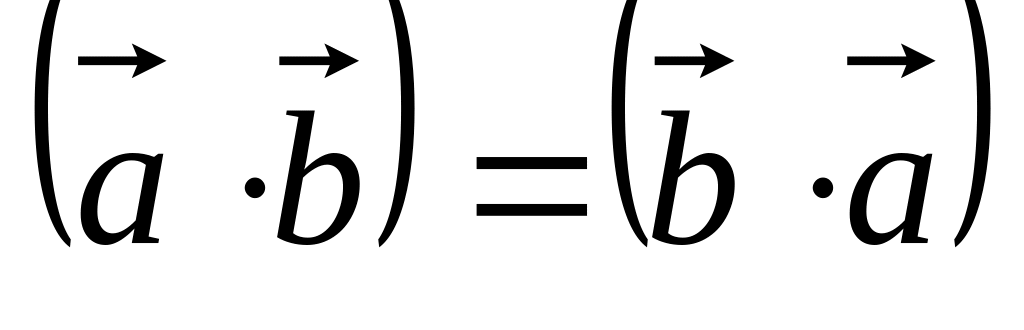 .
.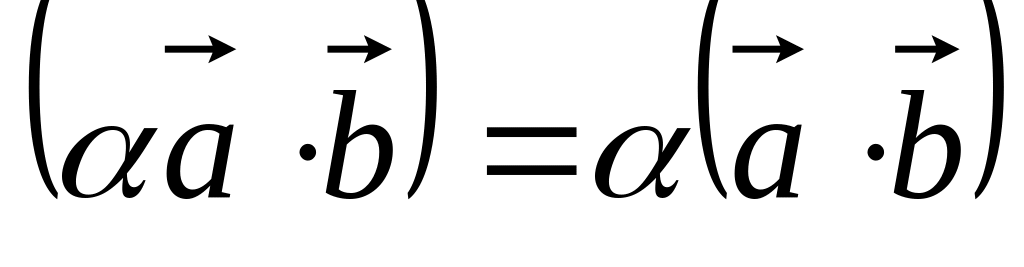 .
.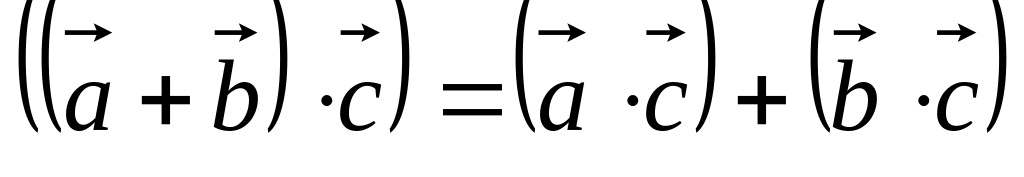 .
.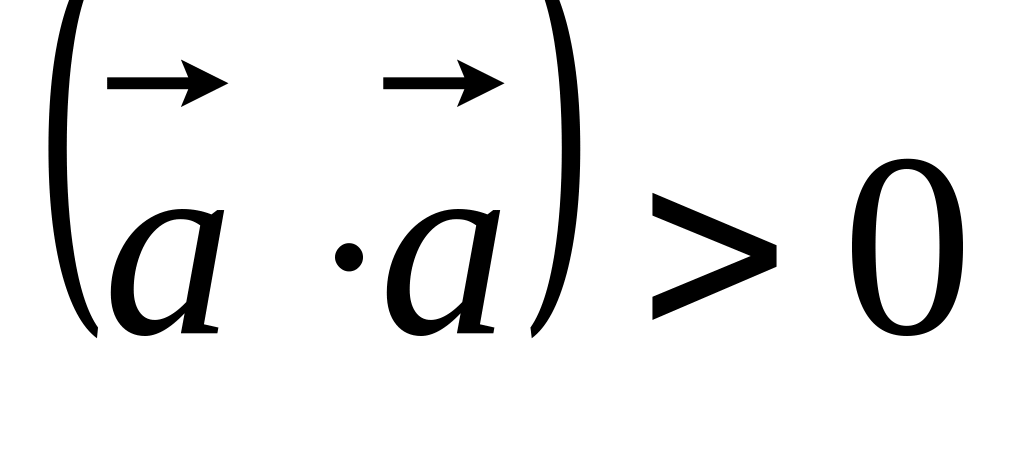 ,
если
,
иначе
,
если
,
иначе
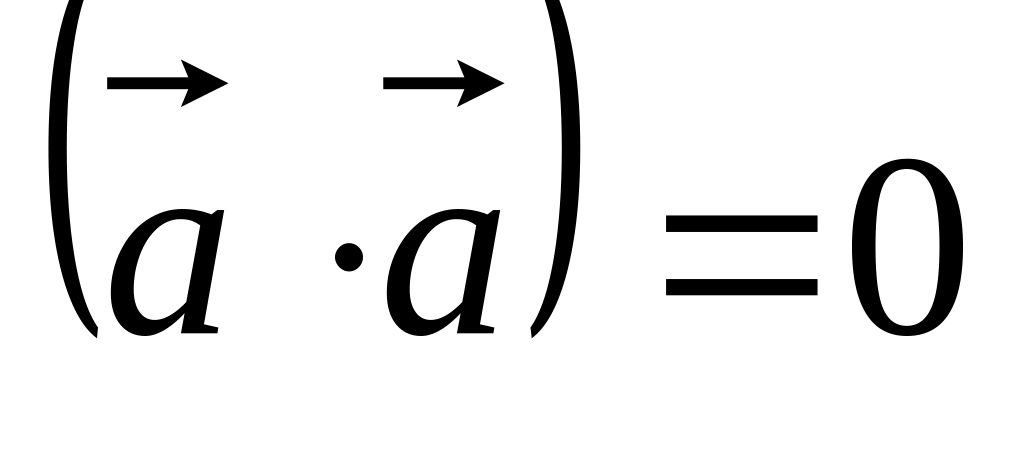 .
.
Необходимое и достаточное условие
ортогональности двух векторов: Для
того чтобы
и
были ортогональны, необходимо и
достаточно, чтобы ![]() .
.
Если или , то теорема справедлива, т.к. нулевой вектор имеет произвольное направление и
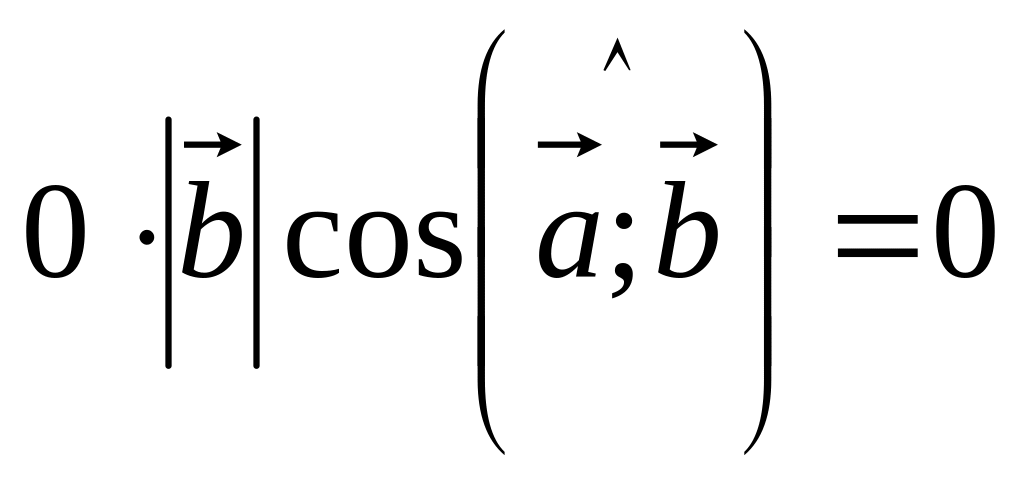 .
.Пусть . Тогда
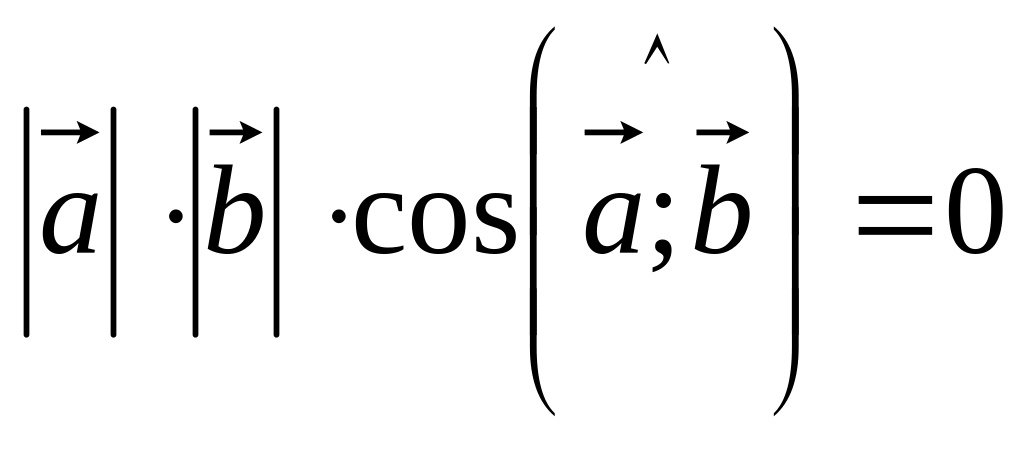 и, т.к.
и
и, т.к.
и
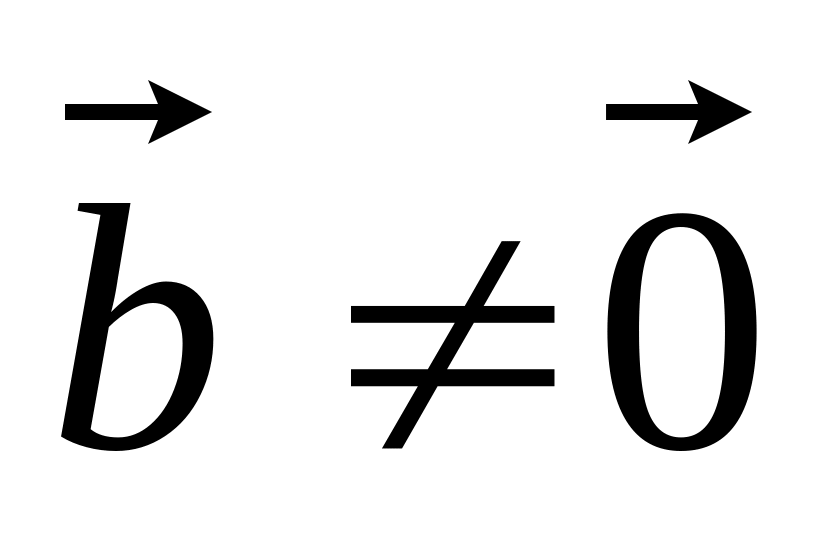 ,
то
,
то
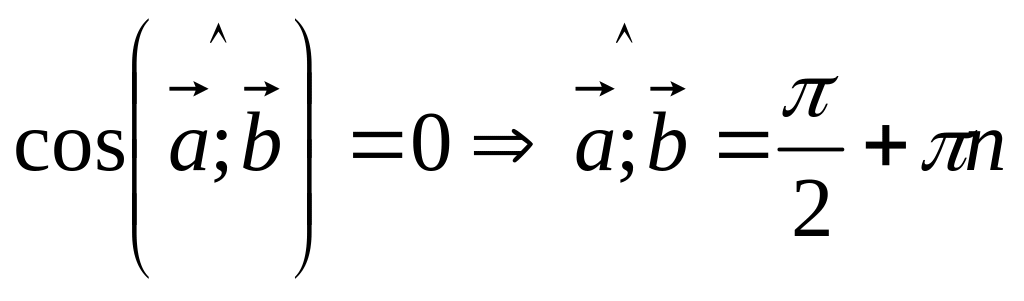 ,
т.е.
,
т.е.
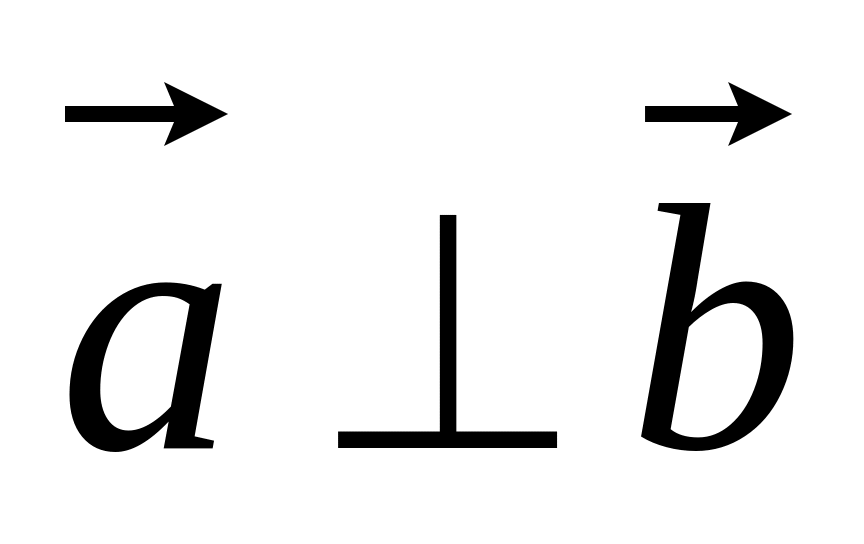 .
.Пусть . Тогда
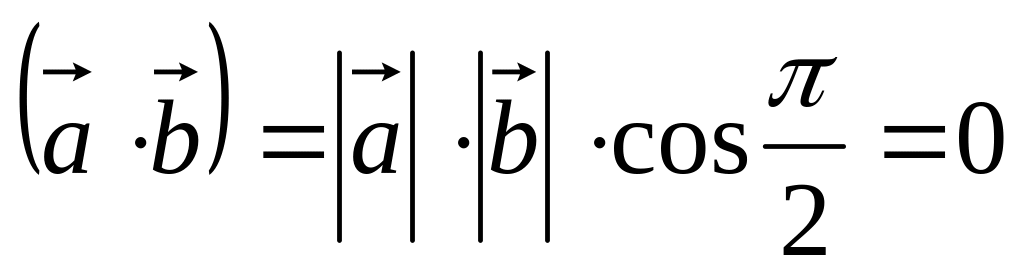 .
.
Пусть задана прямоугольная декартова
система координат
![]() и пусть
и
.
Тогда
и пусть
и
.
Тогда
![]()
![]() ,
т.к.
,
т.к.
![]() ,
,
![]() и
и
![]() .
.
Векторное произведение векторов
Три вектора называют упорядоченной тройкой векторов, если указано, какой из них первый, какой второй и какой третий.
Некомпланарная тройка
векторов
,
и
![]() называется правой (левой) если после
приведения их к общему началу
расположен по ту сторону от плоскости
векторов
и
,
откуда наикратчайший поворот от
к
кажется осуществляемым против (по)
часовой стрелки.
называется правой (левой) если после
приведения их к общему началу
расположен по ту сторону от плоскости
векторов
и
,
откуда наикратчайший поворот от
к
кажется осуществляемым против (по)
часовой стрелки.
Векторным произведение
и
называют вектор
такой, что
![]() ,
,
![]() ,
,
![]() и векторы
,
и
образуют правую тройку. Обозначение:
и векторы
,
и
образуют правую тройку. Обозначение:
![]() .
.
Алгебраические свойства:
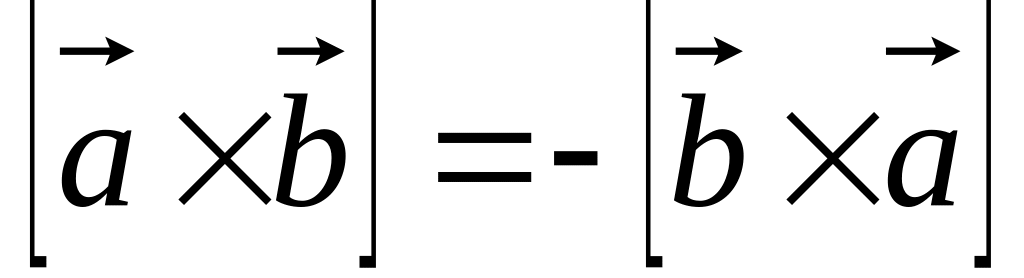 .
.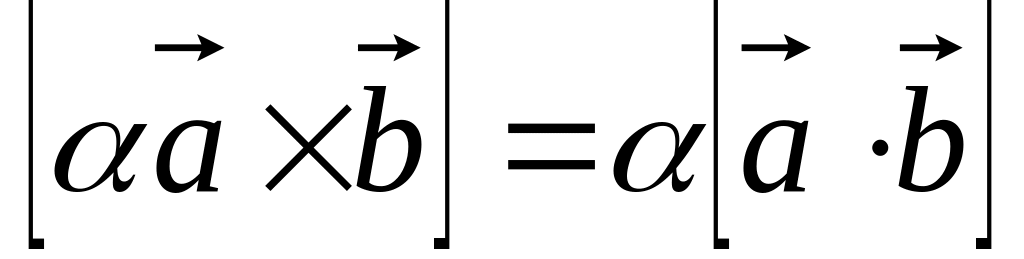 .
.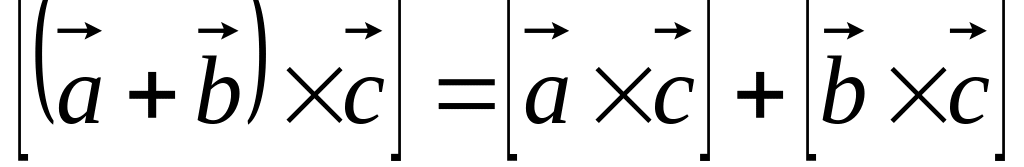 .
.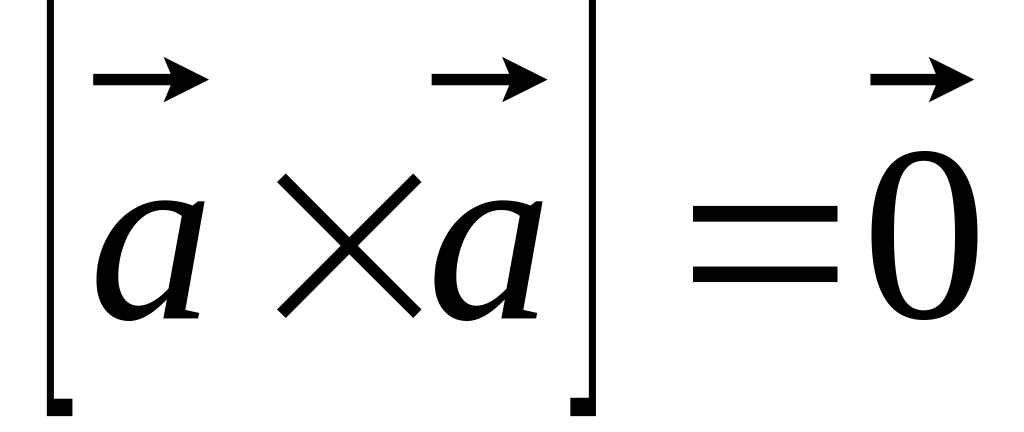 .
.
Необходимое и достаточное
условие коллинеарности двух векторов:
Для того чтобы
![]() ,
необходимо и достаточно, чтобы
,
необходимо и достаточно, чтобы
![]() .
.
Пусть , и . Тогда
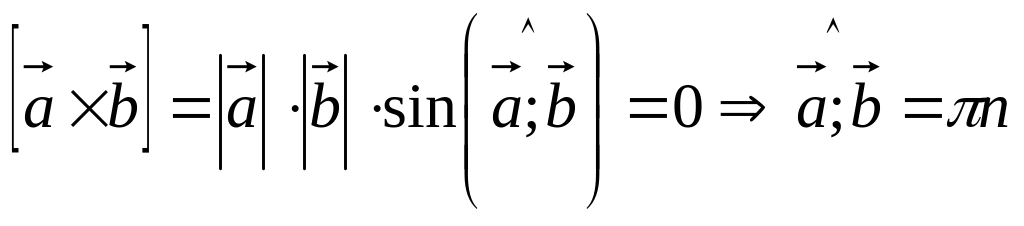 ,
т.е.
.
,
т.е.
.Пусть . Тогда
 .
.
Модуль векторного произведение равен площади параллелограмма, построенного на этих векторах.
![]() .
.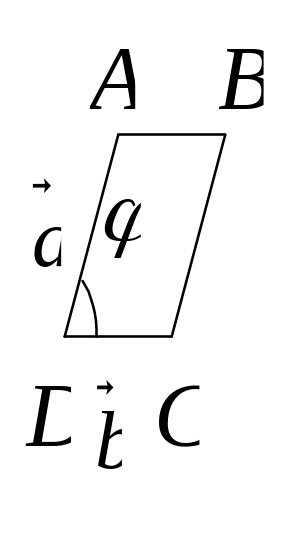
Выражение векторного произведения в ДСК
Если в ДСК
![]() и
и
![]() то
то
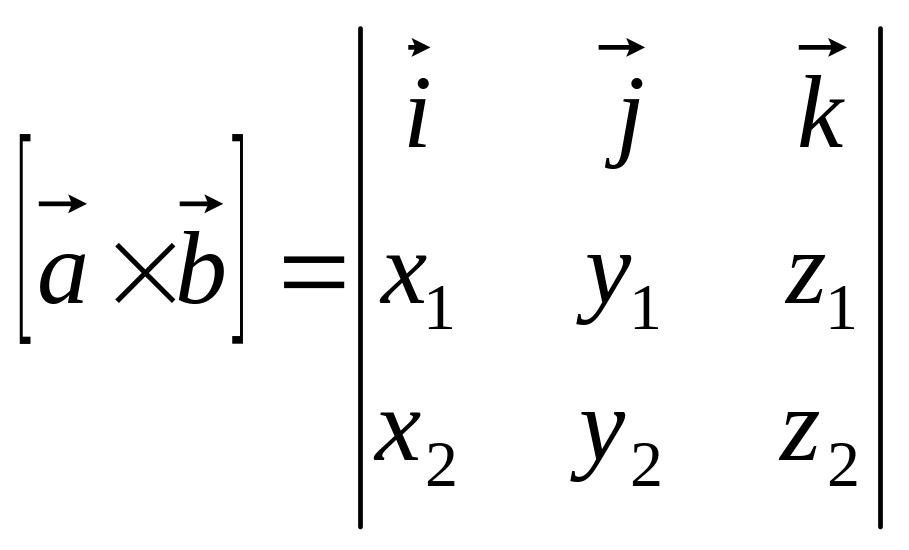 .
.
![]()
![]()
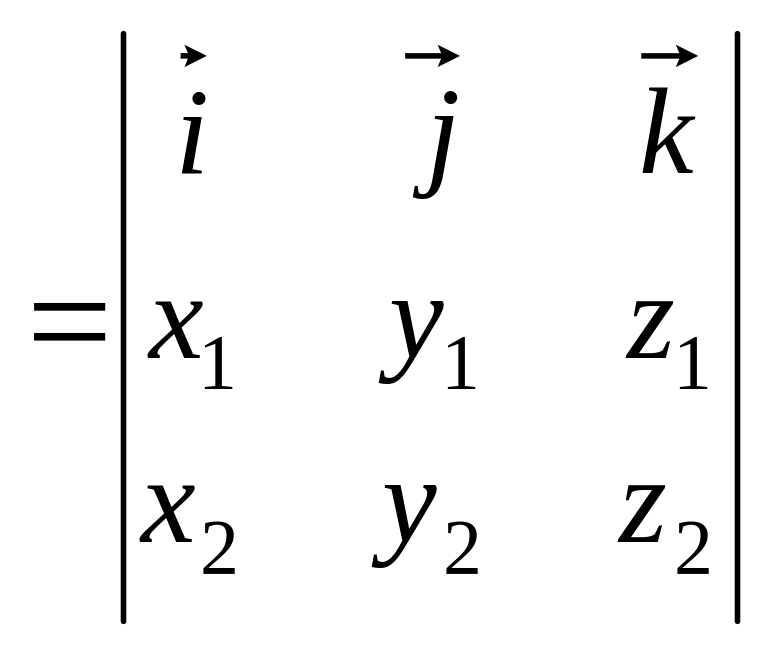 .
.
Смешанное произведение трёх векторов
Смешанным произведением
векторов
,
и
называют число
![]() .
.
Модуль смешанного произведения векторов равен объёму параллелепипеда, построенного на этих векторах после приведения их к общему началу.
![]() ,
,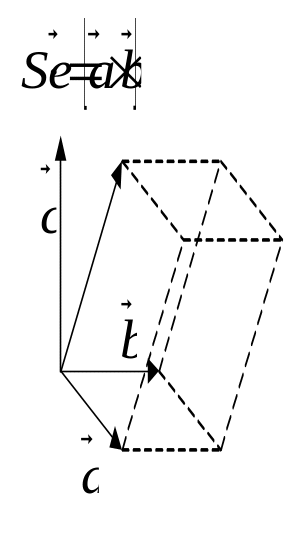 где
где
![]() - орт
- орт
![]() .
.
Пусть в ДСК
,
![]() ,
,
![]() .
Тогда
.
Тогда
![]()
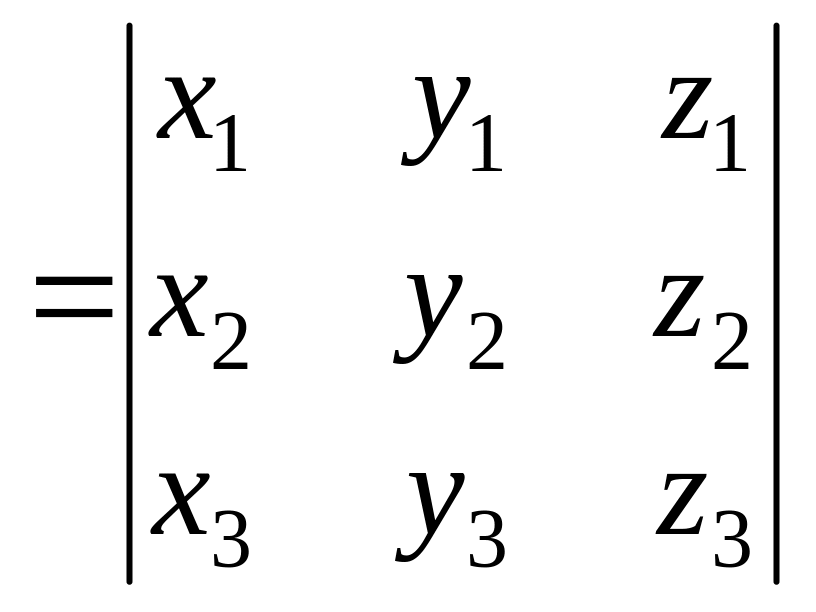 .
.
Критерий компланарности трёх векторов:
Для того чтобы векторы
,
и
были компланарны, необходимо и достаточно,
чтобы
![]() .
.
В самом деле, это означает, что объём параллелепипеда, построенного на этих векторах после приведения их к общему началу, будет равен нулю, а это возможно только когда все три вектора лежат в одной или параллельных плоскостях, т.е. компланарны.
Двойным векторным произведением
векторов
,
и
называют вектор
![]() .
.
![]() .
.
