Обнинский Государственный Технический Университет Атомной Энергетики.

Лабораторная работа № 5.

Тема:

«Изучение поступательного движения на машине Атвуда».

Выполнил:

Проверил:

Обнинск 2003

Цель работы:

Изучение поступательного движения на машине Атвуда, определение ускорения свободного падения опытным путем.

Перечень оборудования:

Машина Атвуда.

Краткая теория.

Поступательное движение тела описывается основным уравнением динамики:

ma=F (1)

Закон движения тела:

x=x₀+(at)²/2

Таким образом, второй закон Ньютона запишется в виде:

Ma₁=Mg – T₁

(M+m)a₂=(M+m)g – T₂ (3).

Основное уравнение вращательного движения:

I = rT₁^’+rT₂^’-N (4).

Поскольку масса нити много меньше масс грузов, её можно считать невесомой, тогда:

T₁=T₁^’ и T₂=T₂^’ (5)

Если считать, что нить нерастяжима и не проскальзывает по блоку, то: -a₁=a₂=a (6)

Угловое и линейное ускорение связаны соотношением:

a= r (7)

Решив совместно систему 3-7 получим:

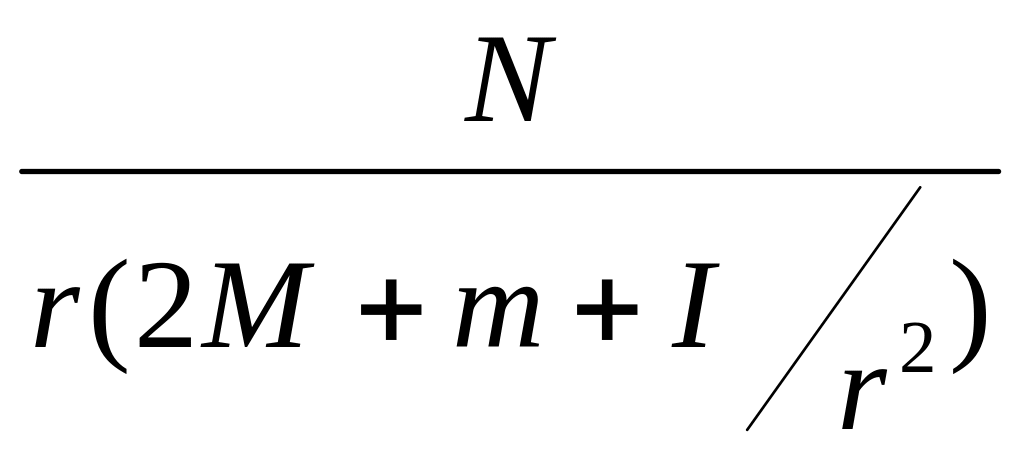a= g - (8)

Для ускорения свободного падения g получим:

g= (9)

Если не учитывать момент инерции блока и момент сил трения, ускорение свободного падения можно определить по приближенной формуле:

g= (10)

Полученное таким образом значение g окажется заниженным. К нему следует добавить поправку:

(11)

Момент сил трения можно определить экспериментально. Помещая на правый груз малые перегрузки, определить массу перегрузка m₀ , при которой начнется движение грузов. Тогда N=rm₀g (12)

С учетом (12) выражение для поправки примет вид:

(13)

В нашей работе ускорение свободного падения определяется по формуле (10) с учетом поправки (13).

Ускорение, используемое в формуле (10), получают в соответствии с законом равноускоренного движения (2):

a= , (14)

где L определяется, как L=x – x₀

Относительная погрешность для a (она является косвенно измеренной величиной) вычисляется следующим образом:

lna=ln =ln2L – lnt²= ln2L - 2lnt ,

(15)

Абсолютная погрешность времени вычисляется по формуле

(16),

где

мм = 10^-3, I=5,77*10^-6 кг*м² , r=41,5 мм , M=68,3 г.

Выполнение работы.

На правый груз положили один из перегрузков и измерили время, в течение которого груз прошел путь L равный 300 мм. Для трех перегрузков повторили опыт 10 раз. Результаты занесли в таблицу №1.

Время:

Таблица №1.

Масса	m1=2,93 г	m2=4,82 г	m3=5,88 г
Nопыта	t1 ,c	t2 ,c	t3 ,c
1	1,808	1,419	1,209
2	1,687	1,405	1,263
3	1,712	1,381	1,166
4	1,675	1,257	1,260
5	1,685	1,347	1,231
6	1,787	1,416	1,223
7	1,682	1,336	1,187
8	1,718	1,318	1,189
9	1,687	1,317	1,210
10	1,829	1,361	1,204
	< t1>=1.726	< t2>=1.356	< t3>=1.214
	1=0,035	2=0,027	3=0,024

Нашли среднее значение <t> по формуле <t>=

<t₁>= =1.726 <t₂>= =1.356 <t₃>= =1.214

Абсолютную погрешность времени вычислили по формуле

и занесли в таблицу №1

Нашли ускорения грузов по формуле a= . Результаты занесли в таблицу №2

Ускорение: ₁

Таблица №2.

Масса	m1=2,93 г	m2=4,82 г	m3=5,88 г
N	a1,	a2,	a3,
1	0,211	0,298	0,410
2	0,214	0,304	0,376
3	0,214	0,380	0,378
4	0,211	0,380	0,378
5	0,188	0,330	0,396
6	0,212	0,299	0,401
7	0,203	0,336	0,426
8	0,211	0,345	0,424
9	0,179	0,346	0,410
10	0,211	0,324	0,414
	<a1>=0,205	<a2>=0,334	<a3>=0,401
	=0,02	=0,02	=0,02

Нашли среднее значение ускорений по формуле <a₁>= и занесли в таблицу №2

Нашли относительные погрешности для ускорений

=0,02; =0,02; =0,02

Ускорения можно записать в виде:

a₁ = 0,205 0,002 a₂ = 0,334 0,002 a₃ = 0,401 0,002

V. Система приходит в движение при массе перегрузка m₀=600*10^-6 кг.

Определим поправку (формула 13):

( )

( )

( )

VI. Вычислим приближенное значение g по формуле 10:

g₁= ( )

g₂= ( )

g₃= ( )

VII. С учетом поправки получаем полное g:

g₁=8,019 +2,241 = 10,26 ( )

g₂=8,489 +1,452 = 9,941 ( )

g₃=8,223 + 1,228 = 9,451 ( )

Таким образом среднее значение g:

<g>= ; <g>= 9,884 ( )

Погрешность вычисления g:

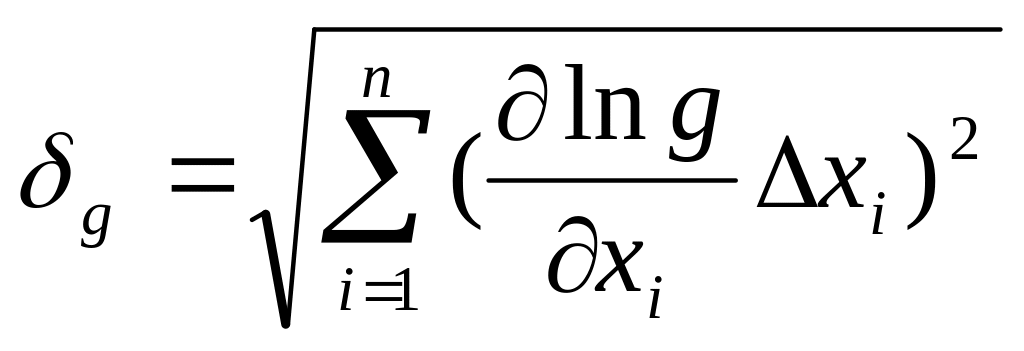, где g= , причем

Тогда =

, = = 0,296 ( )

Таким образом конечный результат представим в виде:

g=9,884 0,296 ( )

Вывод:

Ознакомился с машиной Атвуда. С помощью этой машины экспериментально определил ускорение свободного падения, которое получилось равным

g=9,884 0,296 ( )