НЕФТЯНОЙ ГЕОЛОГИИ

СПБГУАП группа 4736 https://new.guap.ru

квадратный из того механического напряжения, которое развивается в среде на единицу плотности вещества при единичном смещении из положения равновесия.

Если подставить в уравнение (1) функцию x1=Acosωt, где A – постоянная, имеющая размерность смещения x, то найдем, что функция обращает уравнение (1) в тождество.

Решением будет также и функция x2=Bsinωt, где B – постоянная, имеющая размерность смещения “x”. Из теории дифференциальных уравнений известно, что суперпозиция функций x=x1+x2= =Acosωt+Bsinωt

будет также удовлетворять уравнению (1). A и B - постоянные.

Если постоянные A и B можно представить в виде A=asinφ, B=acosφ, где φ – некоторый постоянный угол, то представляя решение как:

x= asinφ cosωt + acosφ sinωt = a(sinφ cosωt + cosφ sinωt) = asin(ωt+φ).

Эта функция в наиболее общем виде представляет решение уравнения Гельмгольца. Постоянная “a“ – есть максимальное значение смещения x, которое при ωt+φ =π/2+2πn

положительна, а при ωt+φ =3π/2+2πn – отрицательна. Смещение рассматриваемой системы осциллирует между значениями ±a.

Угол φ называется фазовой постоянной и измеряется в радианах. Этот угол определяет положение системы в момент времени t=0, то есть, с какого значения амплитуды “a” начинается колебательное движение.

Решение вида x=a sinωt описывает движение только в том случае, если оно начинается из положения равновесия.

Относительное смещение двух систем, колеблющихся с одинаковой частотой, можно характеризовать

разностью их фаз φ1 - φ2 , которая может иметь любую величину, так как одна система может начать движение на несколько периодов раньше или позже чем другая. Когда колебания двух систем диаметрально противоположны,

то они находятся в противофазе и полная разность фаз φ1 - φ2= πn радиан, где n – нечетное число. В случае

идентичных систем, находящихся в фазе, φ1 - φ2= 2πn радиан, где n – любое целое число. Для таких систем смещение, скорость и ускорение одинаковы в любой момент времени.

Скорость и ускорение осциллирующей системы есть функции:

v= dx/dt = x& = aω cos( ωt +φ ) = aω sin (ωt+φ+π/2)

dv/dt = d2x/dt2 = &x& = -aω2 sin( ωt +φ ) = aω2 sin (ωt+φ-π)

Максимальное значение скорости в ωраз, а ускорения в ω2 раз больше амплитуды максимального смещения

“a”. При этом, скорость осцилляций опережает смещение на π/2 радиан, ее максимумы и минимумы достигаются на четверть периода раньше. Если смещение равно нулю, то скорость осцилляций – максимальна и наоборот.

Ускорение же измеряется в противофазе со смещением (сдвинуто по фазе на πрадиан), причем ускорение максимально, когда смещение достигает максимального абсолютного уровня с отрицательной стороны и наоборот.

Если смещение системы изменяется во времени по закону синуса или косинуса, то говорят, что система – линейна. Нелинейность же проявляется в том случае, когда коэффициент жесткости K зависит от величины смещения K = K(x).

Колебательное гармоническое движение дает хорошую иллюстрацию понятию взаимного превращения энергии кинетической в потенциальную и наоборот. Так скорость равна нулю, когда смещение достигает максимума по абсолютной величине, и максимальна, когда смещение равно нулю. В идеальном случае (нет трения) полная энергия остается постоянной:

W = T + П, где W – полная энергия, T – кинетическая, П– потенциальная части полной энергии. В случае

колебаний без потерь W = Tmax = Пmax .

Потенциальная энергия системы есть сумма всех малых частей работы Fdx = Kxdx , где: F – сила возврата в системе на элементе смещения dx, возникающая в системе при смещении на отрезке от 0 до X.

½(ma2ω2), так как [cos(ωt+φ)]max = 1. Но, по предыдущему, mω2 = K, подставив в формулу получим

T = Ka2/2. Отсюда П ≡ T, то есть энергия полностью переходит

4

СПБГУАП группа 4736 https://new.guap.ru

Полная энергия в произвольный момент времени имеет вид:

W = ½(mx2) + ½(Kx2) = ½(ma2ω2[cos2(ωt+φ)]) + ½(Ka2 sin2(ωt+φ)) = ½(Ka2[cos2(ωt+φ) + sin2(ωt+φ)])= ½Ka2, как и должно быть согласно закону сохранения энергии.

1.2. Сложение двух гармонических колебаний.

Во многих случаях простое гармоническое колебание представляют в виде кругового движения. Каждое возможное значение смещения “x” осциллирующей системы при этом суть проекции некоторого радиус-вектора постоянной длины “a” на диаметр окружности описываемой концом этого радиус-вектора при вращении его с

постоянной угловой скоростью “ω” против часовой стрелки. Фазовый угол начала колебаний системы “φ” будет равен в этом случае углу наклона радиус-вектора к диаметру окружности.

Для исследования задач о сложении двух гармонических колебаний воспользуемся этим представлением. 1.2.1 Колебания с одинаковыми частотами.

Пусть движение первой системы описывается функцией x1=a1 sin(ωt+φ1), а второй - соответственно x2=a2 sin(ωt+φ2), где a1 и a2 – амплитуды осцилляций, они не одинаковы, φ1 и φ2 – фазовые углы относительно

общего начала отсчета времени t. Поскольку ни частота, ни амплитуда, ни фазовый угол движения систем не меняются, то в каждый момент времени, если произвести стробоскопическое наблюдение, картина будет одна и та же. Поэтому выводы для какого-то одного, случайно выбранного момента наблюдения, будут справедливы и для

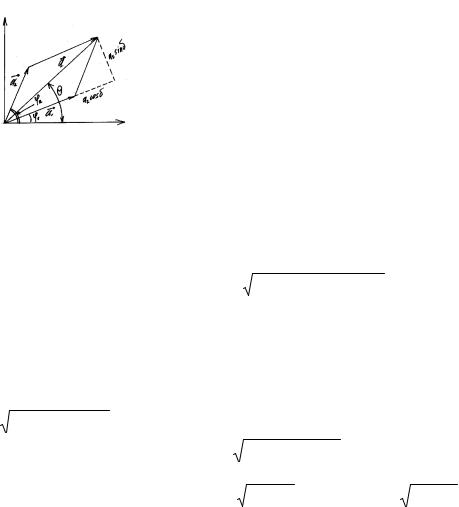
любого другого, то есть, для всего временного промежутка 0 – t. Это заключение дает нам возможность графически изобразить наблюдаемую ситуацию в виде двух векторов a1 , a2 и их суммы ar = ar1 + ar2 . Сумма

двух векторов ar1 и ar2 есть вектор ar численно равный длине диагонали параллелограмма, построенного правилами векторного сложения, приведена на рис.1.

Исследуем полученное выражение. Видно, что суммарное колебание происходит с той же частотой ω , но имеет другой фазовый сдвиг Θ, величина угла этого фазового сдвига лежит между значениями фаз слагаемых ϕ1 и ϕ2 , то есть ϕ1 < Θ <ϕ2 , а вот амплитуда суммарного колебания зависит от разности этих фазовых углов (ϕ2 −ϕ1 = δ ) . Здесь возможны три случая:

квадратному корню из суммы квадратов амплитуд, что больше, чем амплитуда каждого слагаемого, но изменяет фазу колебания. График суммарного колебания выглядит следующим образом Рис. 2.

5

СПБГУАП группа 4736 https://new.guap.ru

Рис. 2.

1.2.2. Колебания с одинаковыми амплитудами, но разными частотами.

Упростим задачу, поставив условие, что эти частоты ω1 иω2 , хотя и не одинаковы, но отличаются друг от друга на малую величину.

ситуация изображена на рис. 3.

Рис. 3.

1.2.3. Сложение двух перпендикулярных гармонических колебаний. а). Колебания с одинаковыми частотами.

x1 = a1 sin(ωt +ϕ1 ) , x2 = a2 sin(ωt +ϕ2 ) . Для нахождения траектории частицы исключим из выражений x1 и x2 параметр t:

6

СПБГУАП группа 4736 https://new.guap.ru

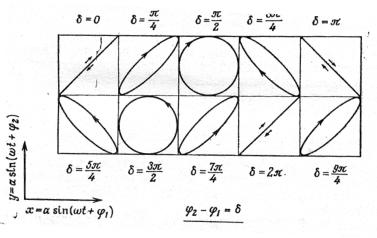
Траектории систем из двух перпендикулярных колебаний приведены на рис.4.

Рис. 4.

Когда ϕ2 −ϕ1 = 0,π,2π,... , оба колебания вырождаются в линию и происходят в одной плоскости.

Такие колебания называют плоско или линейно поляризованными.

Если частоты двух колебаний перпендикулярных и гармонических не одинаковы, то результат их суммы становится более сложным. Траектории соответствующих движений называются фигурами Лиссажу. При этом эти фигуры имеют замкнутый характер и стационарны во времени только в том случае, если частоты двух колебаний

7

СПБГУАП группа 4736 https://new.guap.ru

же фигуры на π / 2 по отношению к предыдущим. Более того, если амплитуды колебаний равны a и b , то фигуры Лиссажу ограничены прямоугольником со сторонами 2a и 2b . Стороны этого прямоугольника всегда касаются рядом точек кривых Лиссажу. При этом отношение количества точек касания лежащих на оси x к числу

Рис.5.

Изучено явление сложения двух колебаний, плоскости которых одни и те же, но происходят они перпендикулярно друг другу. Следствием этой задачи оказывается то, что траектории суммарного движения маятника или частицы меняют свою форму в зависимости от разности фаз этих колебаний. В одних случаях суммарное колебание направлено по одной линии “вперед-назад”, в других – это эллипс, в третьих – окружность.

Кроме того, направление движения частицы определяется тем, какое из колебаний по оси «x» или «y» опережает другое. Это явление носит название “поляризации” колебаний и представляет собой одно из важных понятий многоволновой сейсморазведки.

1.3.4. Сложение большого числа гармонических колебаний.

Найдем сумму достаточно большого числа гармонических колебаний N. Для простоты вывода аналитического выражения ограничимся сложением одинаковых колебательных движений с последовательным сдвигом по фазе одного от другого в сторону ее увеличения. В соответствии с предыдущим, представим каждое гармоническое колебание своим вектором одной и той же длины, но с разными углами наклона к оси x. Таким образом, мы ищем сумму следующего ряда:

a cosωt + a cos(ωt +δ ) + a cos(ωt + 2δ ) + a cos(ωt + 3δ ) +... + a cos[ωt + (N −1)δ ].

Представим это геометрически, как и в п 1.2.1. Сумма будет выражаться длиной вектора соединяющего начало первого и конец последнего векторов, каждый из которых является продолжением предыдущего с поворотом на

один и тот же угол δ . Эта процедура представлена на рис.6.

Опишем из некоторого центра O вокруг полу многоугольника окружность радиусом r и далее имеем:

равнобедренные. Подставим вместо r его выражение через длину одного слагающего сумму вектора a, тогда сумма

будет равна: A = a sin Nδ / 2 . sinδ / 2

Угол ϕ фазового сдвига результирующего сдвига вектора A есть OAB - OAC. Но из ∆AOC:

8

СПБГУАП группа 4736 https://new.guap.ru

фазовый угол суммарного колебания равен половине разности фазовых углов последнего и первого колебаний.

Полностью результирующий вектор запишется теперь в форме: A = a sin Nδ / 2 sinδ / 2

ϕ → 0 .

1.2.5 Сложение большого числа гармонических колебаний со случайной фазой.

9

СПБГУАП группа 4736 https://new.guap.ru

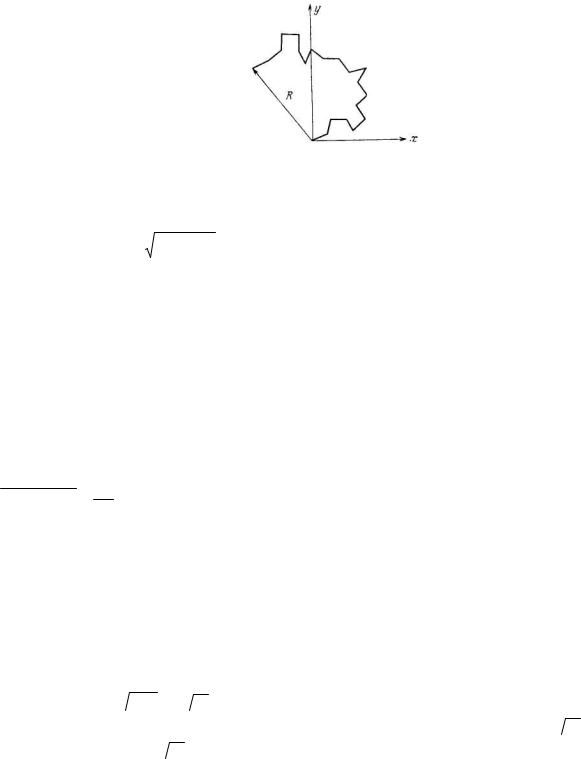
Рассмотрим вопрос о суммировании N одинаковых по амплитуде колебаний, но обладающих случайной фазой. Воспользуемся геометрическим изображением и правилом суммирования векторов из предыдущего

параграфа. Пусть необходимо найти сумму N векторов, длинной a и фазовыми углами ϕi .

.

Рис. 8.

На рис. 8 представлено изображение этой суммы. Из этого рисунка можно заключить, что в этот многоугольник нельзя вписать окружность, как, впрочем, и описать ее. Поэтому остается только один вариант: разложить каждый

вектор на его составляющие по осям x и y и найти их сумму по отдельности, а затем вычислить длину вектора по известной формуле: A = Ax2 + Ay 2 , где: Ax и Ay – суммы проекций векторов Аi на оси x и y соответственно.

обобщенная запись удвоенного произведения вида 2cosϕi cosϕj , которое принимает случайным образом значения от –1 до +1, в том числе и 0. Усредним эту сумму по углам ϕi , изменяющимся от 0 до 2π .

1 2π

cosϕi cosϕ j = 2π ∫0 cosϕi cosϕjdϕ = 0 , при i.≠j, так как это есть сумма знакопеременного ряда. Однако,

остаются члены, когда i=j, что дает следующие соотношения:

Следовательно, A = Na2 = a N . Амплитуда системы, участвующей в N одинаковых гармонических колебаниях с одинаковой частотой и амплитудой, но случайно распределенными фазами равна a N и по

сравнению с предыдущим в N раз меньше той же суммы, тех же маятников при последовательно изменяющихся фазах

1.2 Затухающие гармонические колебания.

Выше рассмотрены случаи гармонических колебаний, когда полная энергия системы сохраняется бесконечно долгое время, а смещение изменяется по закону синуса или косинуса неограниченное время. В действительности некоторая доля энергии колеблющегося тела всегда рассеивается вследствие действия сил противодействующих движению. Наличие такого противодействия означает, что наряду с силой противодействия действуют другие силы, величину которых принимают пропорциональной скорости движения. Теперь новое уравнение баланса сил

10

СПБГУАП группа 4736 https://new.guap.ru

или уравнение движения принимает следующий вид: m&x&= −βx& − Kx , где K – упругость возвращающей силы, β

– постоянный коэффициент, равный силе сопротивления, приходящейся на единицу площади. Наличие такого слагаемого в уравнении всегда дает потерю энергии. Задача заключается в том, чтобы найти решение однородного

из курса дифференциальных уравнений, решение можно искать в виде: x = Ceαt , где C,α - также постоянные. C - размерность длины, а α - размерность – обратная времени. Подставляя в уравнение, получаем следующее выражение: Ceαt (mα2 + βα + K) = 0 . Здесь возможны два случая. Первый Ceαt = 0 , но eαt всегда >0 при любом t откуда следует ,что C = 0 . Это значит, что система находится в состоянии покоя (стоит). Нам интересен все же динамический вариант, когда C ≠ 0 . Для выполнения этого условия необходимо положить равенство 0