сейсморазведка часть 1

СПБГУАП группа 4736 https://new.guap.ru

Соответственно цилиндрические волны те, которые имеют поверхности разных фаз в виде цилиндров с общей для них центральной осью.

Плоские волны это такие, которые поверхности равных фаз образуют в виде плоскостей бесконечной протяженности по осям x и y ; z, y или x, z . Эти волны описываются наиболее простыми математическими

выражениями. Для них поток энергии через поверхность равных фаз есть const , потому что сама поверхность не изменяется в процессе распространения.

При больших расстояниях от центра и оси симметрии сферические и цилиндрические волны переходят в плоские вследствие уменьшения кривизны фронтов. Обычно уже на расстоянии 10λ длин волн от центра симметрии приближение плоских волн правомочно.

Необходимо усвоить и запомнить один принципиально важный момент. Отдельные осцилляторы, составляющие среду, не распространяются вместе с волнами, а только колеблются около положения равновесия или покоя, в поперечном, продольном или комбинированном направлениях. Мы наблюдаем в качестве волн только фазовые соотношения между ними: какой из осцилляторов уже начал, какой закончил, а какие и не приступали к процессу колебательного движения. Поэтому в отличие от колебательного процесса, волновое движение характеризуется тремя скоростями.

1. Скорость нарастания или спадания смещения иначе массовая скорость. Это есть скорость гармонических колебаний осциллятора с данной частотой, около положения равновесия. Эта скорость в

волне соответствует скорости чисто колебательного процесса, т.е. du / dt

2.Волновая скорость. Эта величина характеризует быстроту распространения в среде одинаковой фазы колебательного процесса осцилляторов, то есть какого-то горба или впадины. Она носит название фазовой скорости, имеет кинематический смысл и является самой быстрой из всех скоростей передачи информации в среде о данном колебательном процессе.

3.Скорость распространения группы однотипных волн с различными частотами и амплитудами, составляющими волновой импульс или волновой пакет. Эта величина носит название групповой скорости и определяет скорость передачи энергии колебательного процесса через среду, то есть определяет, как быстро

от одного осциллятора другому передается энергия вида Kx2 / 2 .

Если волна одна и она гармоническая, то vФ≡ vГР . Этов свою очередь является показателем поведения среды в случае малых возмущений параметров ее состояния и определяет отклонение от закона линейной упругости среды.

форму □U=0.Это уравнение связывает ускорение гармонического осциллятора с силой сопротивляющейся возмущению в состоянии этого осциллятора, то есть это выражает математически действие второго закона Ньютона в сплошной среде.

2.5. Решение волнового уравнения.

Опять-таки, мы не будем рассматривать процедуру получения волнового уравнения. Запишем сразу, что решение этого уравнения является функцией U = f1 (ct − x) + f2 (ct + x) . Здесь U - смещение в точке “ x ” в момент времени t осциллятора, совершающего простые гармонические колебания. Представим функцию f в

виде a sin( ω t − ϕ ) , подставив в уравнение, убеждаемся, что эта функция является его решением, так как удовлетворяет ему при всяких x и t .

Аргумент f − (ct − x) - имеет размерность длины. Но для того, чтобы эта функция могла быть sin или

cos необходимо, чтобы аргумент ее был безраздельным и выражался бы в ряд, то есть имел размерность угла. По этой причине аргумент ct − x необходимо умножить на функцию с размерностью обратной длины. Выберем

числом, имеет размерность обратной длины. Этот коэффициент указывает, какое число длин волн укладывается на расстоянии от начала колебания до того момента, когда в процесс вступил осциллятор с координатой x .

26

СПБГУАП группа 4736 https://new.guap.ru

Теперь посмотрим на простую гармоническую волну вида: y = a sin(ωt −ϕ) и сравним ее с решением

t = 0 сфотографировать волновой процесс, то мы получим траекторию смещения вида:

Значит, если некоторый осциллятор, расположен справа от точки x0 , то он начнет свое колебательное движение с запаздыванием, позже, чем осциллятор в точке x0 . Запаздывание это равно 2λπ (x − x0 ) . Если

x − x0 = λ , то запаздывание ϕ = 2π - то есть полному периоду колебаний осциллятора в точке x0 . Этим

рассуждением мы определяем λ - как длину волны, а именно расстояние между осцилляторами, имеющими разность фаз 2π радиан.

Из выражения 2λπ c = ω = 2πν находим, что c =νλ - волновая или фазовая скорость, равная

произведению частоты на длину волны. Или λ / c =1/ν = T - период колебаний, показывающий, что волна проходит расстояние в одну λ за время T . Мимо наблюдателя за 1 сек. проходит цуг колебаний, содержащий ν длин волн и имеющий длину численно равную фазовой скорости c .

Существует несколько эквивалентных форм записей функции f (ct − x) , например, для синуса:

U = a sin 2λπ (ct − x) U = a sin 2π(νt − λx )

U = a sinω(t − cx ) U = a sin(ωt − kx)

U = aei(ωt−kx)

Фазовая скорость конечно равна c = dx / dt и есть скорость движения фазы (ωt − kx) вдоль цепочки осцилляторов.

Скорость колебательного смещения самого осциллятора после прихода фазы есть dU / dt - простая гармоническая скорость. Обычно она задается источником возмущения.

Возьмем частные производные dydt и dydx , будем иметь: dydt = aω cos(ωt − kx) ;

dydx = −ak cos(ωt − kx) и cos(ωt − kx) = dydt a1ω ; dydx = −ak dydt a1ω ; dydt = −ωk dydx = −c dydx = = − dxdt dydx . Таким образом, скорость частицы во фронте волны равна произведению волновой скорости

c = dx / dt на градиент волнового профиля dU / dx , взятого со знаком минус.

Скорость частиц возрастает в том же направлении, в котором растет поперечная сила в струне, т.е. в сторону горба или впадины. Рис. 18.

27

СПБГУАП группа 4736 https://new.guap.ru

Рис. 18

Импеданс струны.

Любая среда сопротивляется изменению своего первоначального состояния, в том числе и волновому процессу, хотя бы уже потому, что происходит ее нагревание. Это сопротивление удобно описывать импедансом или “волновым сопротивлением”. Если среда пропускает волны без потерь и не имеет механизма поглощения энергии, то импеданс действителен и определяется двумя параметрами, описывающими процесс накопления энергии в среде: инерций и упругости. При наличии потерь в выражении импеданса появляется мнимый добавок. Так и для струн. В соответствии с природой волн импеданс среды для поперечных волн определяется как отношение

возбуждается поперечной силой F = F0eiωt , натяжение постоянно и равно T . Запишем баланс сил для этого конца: рис. 19.

Рис. 19.

плотность (масса на единицу длины).

2.6. Отражение и прохождение поперечных волн через границу двух сред.

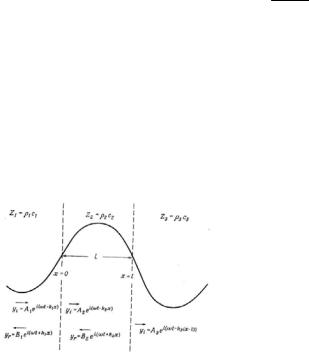
Спросим себя, как будут реагировать поперечные волны на резкое изменение импеданса силы? Пусть наша струна состоит из двух кусков, гладко соединенных в точке x = x0 и имеет постоянное

натяжение T . Обе струны имеют ρ1 и ρ2 и следовательно разные волновые скорости c12 = T / ρ1 и c22 = T / ρ2 . Импедансы их Z1 = ρ1c1 и Z2 = ρ2c2 .Рис. 20.

28

СПБГУАП группа 4736 https://new.guap.ru

Рис. 20.

Волна, распространяющаяся слева направо в точке x = x0 , встречает скачок импеданса Z . Положим, что x0 = 0 . Тогда в этой точке образуются дополнительно две волны. Отраженная Ur и проходящая Uτ . Пусть смещение в падающей волне . Смещение в отраженной волне будет . Смещение прошедшей волне Uτ = cτ ei(ωt−kxi) . Найдем выражение для b и c . Наложим граничные условия в точке

x= x0 = 0 . Их должно быть два.

1.Геометрическое – в любой момент t полное смещение справа и слева от точки x0 - одинаковы.

2.Динамическое - поперечная сила непрерывна в точке x0 .

Теперь будем иметь:

Ui =Ur =Uτ .

−ρ1c1a + ρ1c1b = −ρ2c2c или, учитывая, что ρc = z .

(2)Z1 (a − b) = Z2c объединяя с (1) получаем систему :

b / a - амплитудный коэффициент отражения.

Они не зависят от ω , не вносят фазовых искажений и c / a - амплитудный коэффициент пропускания. сдвигов за исключением сдвига на π при Z2 > Z1 .

При Z2 = ∞- закрепленный конец струны b / a = −1; c / a = 0 падающая волна полностью отражается ac − ab =1.

При Z2 = 0 -свободный конец, имеем b / a =1, а c / a = 2 , то есть амплитуда волны на свободном

конце удваиваются.

Что происходит в этом случае с энергией волны?

Энергия единичного отрезка струны равна: e = 12 ρω2a2 , где ω - частота, а – амплитуда смещения. Каждый единичный отрезок начинает колебаться с приходом волны, а волна распространяется со скоростью c , то и

29

СПБГУАП группа 4736 https://new.guap.ru

Скорость, с которой энергия расходуется в точке x0 , т.е. уносится отраженной и преломленной волнами будет: 12 ρ1c1ω2b2 + 12 ρ2c2ω2c2 = 12 Z1ω2b2 + 12 Z2ω2c2 . Поскольку энергия сохраняется, то

отражается.

§ Согласование импедансов.

Этот прием имеет важное практическое значение в вопросах передачи и приема сейсмических колебаний. Хотя, довольно странное занятие согласование двух геологических сред на глубине, поскольку их характеристики заданы природой от сотворения мира. Между тем, этот вопрос возникает всегда при проведении практических полевых наблюдений за законами распространения упругих волн, поэтому изучим его более внимательно.

На примере трех струн, жестко и гладко соединенных между собой покажем, как можно избежать

появление отраженной поперечной волны. Мы хотим добиться, чтобы Wпрох/Wпад= Z3 D2 =1.

Z1 A2

Согласно типичным условиям из § 1 запишем, что происходит в сечениях x = 0 и x = l , где l - длина вставного куска струны:

1) Aei(ωt−k1x) + Bei(ωt+k1x) = Cei(ωt−k2 x) + Dei(ωt+k2 x) или как и ранее:

A + B = C + D - это первое уравнение при x = 0 .

2) T (−ik1 A + ik1B) = T (−ik2C + ik2 D) и получим Z1 ( A − B) = Z2 (C − D) .

Первое условие в точке x = l даст: Ce−ik2l + Deik2l = E и Z2 (Ce−ik2l − Deik2l ) = Z3 E эти получаются из того, что, используя форму струны при x = l будем иметь: из рис.21.

Рис.21.

U пад = Aexp[−i(ωt − k1 x)] U1 отр = B exp[−i(ωt + k1 x)] U1 прох= C exp[−i(ωt − k2 x)] U2 отр= D exp[−i(ωt + k2 x)]

U3 прох= E exp[−i(ωt − k3 x1 )] , где x1 = x − l при x2 = l и x1 = 0 .

Таким образом, получим четыре уравнения:

30

СПБГУАП группа 4736 https://new.guap.ru

Если импеданс связывающей среды равен среднему геометрическому двух других импедансов, которые должны быть согласованы, а длина (мощность) связываемых линий равна λ2 / 4 , где λ2 = 2π / k2 четверти

длины волны в промежуточной среде, то вся энергия с частотой ω = c / λ2 будет свободно проходит в третью среду.

2.6.Волновые пакеты.

Впредыдущих параграфах мы рассматривали монохроматические волны, имеющие одну частоту ωi и

одну длину волны λi . Более общим, а для сейсморазведки и единственным пока случаем, является тот, когда волны образуют некоторый конечный набор или группу разно частотных гармоник. В природе это присутствует в

o o

виде белого дневного света, где λmax = 7000 A- красный, а λmin = 2500 A - синий или фиолетовый. Здесь

31

СПБГУАП группа 4736 https://new.guap.ru

λmax ≈ 2,6 − 2,7 раза. Для сейсмических частот имеем: ωmin =10 Гц, ωmin =125Гци отношение их будет

λmin

12,5, что в 5 раз больше чем у видимого света.

Рассмотрим пакет из двух волн с одинаковыми амплитудами A , но с близкими частотами ω1 и ω2 . u1 = Acos(ω1t − k1 x);u2 = Acos(ω2t − k2 x) . Сложим их: