
- •Установочная лекция 4 (2 ч.) комплексный метод анализа электрических цепей
- •4.1А. Комплексный метод расчета цепей синусоидального тока
- •4.1Б. Комплексная схема замещения электрической цепи
- •4.1В. Закон Ома и законы Кирхгофа в комплексной форме
- •Первый закон Кирхгофа (1зк) гласит, что в любом узле комплексной схемы замещения цепи алгебраическая сумма комплексов токов равна нулю, т.Е.
- •1. Выбираем направления комплексов токов ветвей и обозначаем их стрелками на схеме (см. Рис. 4.3).
- •3. Составляем уравнение по 1зк для узла 1:
- •4. Выбираем независимые контуры и направление обхода контуров по часовой стрелке. В нашем упражнении имеется два независимых контура (левый и средний).
- •4.1Д. Анализ цепи с последовательно-параллельным соединением ветвей
- •4.1Д. Комплексная мощность и баланс мощностей в сложной цепи
- •Разделы для самостоятельной проработки
- •Литература и информационные источники
4.1В. Закон Ома и законы Кирхгофа в комплексной форме
Для ветви с пассивными элементами при совпадении условно положительных направлений тока и напряжения выражение закона Ома имеет вид
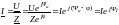 ,
,
где Z = Zej комплекс сопротивления ветви.
Если > 0, то ток отстаёт по фазе от напряжения, при < 0 ток опережает по фазе напряжение.
Так как полная комплексная проводимость Y = 1/Z, то ток
I
= UY
= UYe .
.
Запишем обобщённый закон Ома для ветви с n последовательно соединёнными источниками напряжения и пассивными элементами:
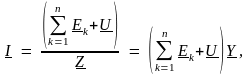
где Еk и U комплекс k-й ЭДС и комплекс напряжения на зажимах ветви; при этом знак плюс записывают при совпадении направлений ЭДС и напряжения c направлением тока ветви, а знак минус при их противоположном направлении.
Первый закон Кирхгофа (1зк) гласит, что в любом узле комплексной схемы замещения цепи алгебраическая сумма комплексов токов равна нулю, т.Е.
 .
.
Условимся комплексы токов, направленные к узлу, записывать со знаком плюс, а комплексы токов, направленные от узла, записывать со знаком минус.
Второй закон Кирхгофа (2ЗК) гласит, что в любом контуре схемы цепи алгебраическая сумма комплексов ЭДС равна алгебраической сумме комплексов напряжений на пассивных элементах этого контура, т.е.

где (n) и (m) число ЭДС и пассивных элементов в выбранном контуре.
Комплексы ЭДС и комплексы напряжений (токов) на пассивных элементах контура записывают со знаком плюс, если их направления совпадают с направлением обхода контура.
 Упражнение
4.1.
Составить необходимое число уравнений
методом законов Кирхгофа относительно
неизвестных комплексов токов
ветвей (I1,
I2
и I3)
схемы цепи (рис.
4.3).
Упражнение
4.1.
Составить необходимое число уравнений
методом законов Кирхгофа относительно
неизвестных комплексов токов
ветвей (I1,
I2
и I3)
схемы цепи (рис.
4.3).
1. Выбираем направления комплексов токов ветвей и обозначаем их стрелками на схеме (см. Рис. 4.3).
2. Уточняем число узлов (У = 2) и ветвей (В = 3) схемы цепи с неизвестными токами.
3. Составляем уравнение по 1зк для узла 1:
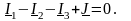
4. Выбираем независимые контуры и направление обхода контуров по часовой стрелке. В нашем упражнении имеется два независимых контура (левый и средний).
Внимание! Ветвь с заданным комплексом тока J источника тока в уравнениях, составляемых по 2ЗК, не учитывается.
Запишем уравнения по 2ЗК (для независимых контуров):


4.1г. Анализ цепи с параллельным соединением элементов R, L и C между собой и с источником синусоидального напряжения u = Umsint (рис. 4.4а).
Комплекс тока I на входе цепи может быть найден по 1ЗК, как сумма комплексов токов ветвей: I = IR + IL + IC, определённых по закону Ома:
IR = U/R = gU, IL = U/jXL = jbLU, IC = U/(-jXC) = jbCU,
г де
g
= 1/R,
bL
=
1/XL,
bС
= 1/XС
модули
проводимостей идеализированных
двухполюсных элементов R,
L
и C,
или
как произведение комплекса входного
напряжения U
и комплекса входной проводимости Y,
т.е.
I
=
YU,
где Y
= Y1
+
Y2
+ Y3
= g
jbL
+ jbC.
де
g
= 1/R,
bL
=
1/XL,
bС
= 1/XС
модули
проводимостей идеализированных
двухполюсных элементов R,
L
и C,
или
как произведение комплекса входного
напряжения U
и комплекса входной проводимости Y,
т.е.
I
=
YU,
где Y
= Y1
+
Y2
+ Y3
= g
jbL
+ jbC.
Векторная диаграмма входного напряжения и токов цепи при XL > XС приведена на рис. 4.4б, где IR и jIX = jIС jIL – активная и реактивная составляющие комплекса тока I цепи; = arctg(IX/IR).
При параллельном соединении ветвей, содержащих как один, так и несколько последовательно соединённых пассивных элементов (рис. 4.5а), комплекс входного тока также находят в виде суммы предварительно найденных комплексов токов ветвей, т.е. I = I1 + I2 + I3 (рис. 4.5б), где:
I1
= U/Z1,
I2
= U/Z2,
I3
= U/Z3,
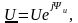
 ,
,
 ,
,

 или
в виде произведения заданного
комплекса напряжения U
и
комплексной входной проводимости цепи
Y,
т. е. I
= YU,
где Y
= Y1
+ Y2
+ Y3;
Y1
=
=
1/Z1,
Y2
=
1/Z2,
Y3
=
1/Z3.
или
в виде произведения заданного
комплекса напряжения U
и
комплексной входной проводимости цепи
Y,
т. е. I
= YU,
где Y
= Y1
+ Y2
+ Y3;
Y1
=
=
1/Z1,
Y2
=
1/Z2,
Y3
=
1/Z3.
