
- •Установочная лекция 4 (2 ч.) комплексный метод анализа электрических цепей
- •4.1А. Комплексный метод расчета цепей синусоидального тока
- •4.1Б. Комплексная схема замещения электрической цепи
- •4.1В. Закон Ома и законы Кирхгофа в комплексной форме
- •Первый закон Кирхгофа (1зк) гласит, что в любом узле комплексной схемы замещения цепи алгебраическая сумма комплексов токов равна нулю, т.Е.
- •1. Выбираем направления комплексов токов ветвей и обозначаем их стрелками на схеме (см. Рис. 4.3).
- •3. Составляем уравнение по 1зк для узла 1:
- •4. Выбираем независимые контуры и направление обхода контуров по часовой стрелке. В нашем упражнении имеется два независимых контура (левый и средний).
- •4.1Д. Анализ цепи с последовательно-параллельным соединением ветвей
- •4.1Д. Комплексная мощность и баланс мощностей в сложной цепи
- •Разделы для самостоятельной проработки
- •Литература и информационные источники
4.1Б. Комплексная схема замещения электрической цепи
Компонентные уравнения пассивных элементов в комплексной форме дают возможность изобразить комплексную схему замещения электрической цепи, составить и решить алгебраические уравнения относительно комплексов электрических величин, затем осуществить обратный переход от комплексов к синусоидальным функциям.
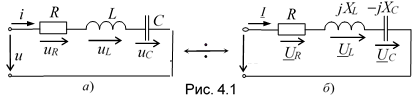
Найдём комплекс сопротивления и ток последовательной RLC-цепи (рис. 4.1а), к зажимам которой приложено напряжение u = Um sin(t + u).
 Воспользовавшись
компонентными уравнениями элементов,
вычертим комплексную
схему замещения цепи
(рис. 4.1б).
Запишем соответствия электрических
величин для схем рис. 4.1а,
б:
Воспользовавшись
компонентными уравнениями элементов,
вычертим комплексную
схему замещения цепи
(рис. 4.1б).
Запишем соответствия электрических
величин для схем рис. 4.1а,
б:
u(t)
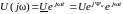 ,
где U
=
,
где U
=
 ,
,
uR(t)
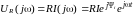 ,
где I
=
,
где I
=
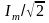 ,
,
uL(t)
UL(j)
= jLI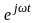 = jXLI
,
= jXLI
,
uС(t)
UС(j)
=
j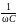 I
=
jXСI
,
I
=
jXСI
,
где jXL и jXС комплексы индуктивного и ёмкостного сопротивлений.
Согласно второму закону Кирхгофа для схемы рис. 4.1а имеем
uR
+
uL
+
uC
=
Ri + L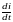 +
+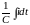 =
u = Umsin(t
+ u).
=
u = Umsin(t
+ u).
Подставив
в уравнение вместо напряжения u,
тока i,
его производной d[(t)]/dt
и
интеграла
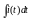 соответствующие комплексные выражения,
получим
соответствующие комплексные выражения,
получим
RI(j) + jXLI(j) jXCI(j) = U(j) ,
RI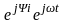 +
jLI
+
jLI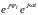
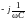 I
I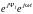 =
U
=
U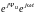 .
.
Сократив
левую и правую части на множитель
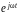 и преобразовав, получим
выражение
тока в комплексной форме
и преобразовав, получим
выражение
тока в комплексной форме
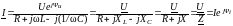 ,
,
в котором все комплексные величины (I, U и Z) не зависят от времени.
Итак, комплекс тока I последовательной RLC-цепи равен комплексу напряжения U, делённому на комплексное число
Z = R + jXL jXC = R + jX = Zej,
носящее название комплекс сопротивления последовательной RLC-цепи, где:
Z =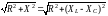 и
=
u
i
=
arctg
и
=
u
i
=
arctg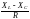
модуль и аргумент комплекса сопротивления Z ; jX = jXL jXC комплекс реактивного сопротивления RLC-цепи.
Оригинал тока i(t) получим, осуществив обратный переход от комплекса тока I к его оригиналу, т.е.
I
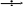 i(t)
=
i(t)
=
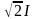 sin(t
+
i)
= Imsin(t
+
i).
sin(t
+
i)
= Imsin(t
+
i).
Для наглядного отображения соотношений между электрическими величинами комплексной схемы замещения (см. рис. 4.1б) построим диаграмму тока (при i = 0) и напряжений цепи в комплексной плоскости Re-Im (рис. 4.2а) в соответствии с уравнением
R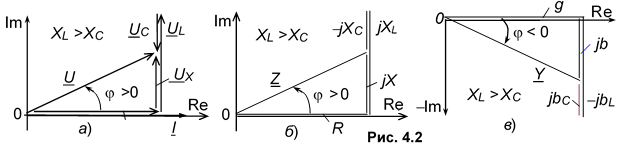 Ie
Ie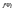 +
jLIe
+
jLIe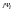
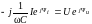
(без
оператора
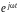 ,
т.е. при
t
=
0),
в которой вектор напряжения UR
= RI
совпадает
по фазе с вектором тока I,
вектор напряжения UL
= jXLI
опережает
его по фазе на угол /2,
а вектор напряжения UC
=
jXCI
отстает
по фазе от вектора тока I
на угол /2.
Вектор UX
= UL
UC.
,
т.е. при
t
=
0),
в которой вектор напряжения UR
= RI
совпадает
по фазе с вектором тока I,
вектор напряжения UL
= jXLI
опережает
его по фазе на угол /2,
а вектор напряжения UC
=
jXCI
отстает
по фазе от вектора тока I
на угол /2.
Вектор UX
= UL
UC.
Вектор напряжения U опережает вектор тока I по фазе на угол .
Поделив комплексы напряжений (см. рис. 4.2а) на комплекс тока I, получим треугольник сопротивлений RLC-цепи (рис. 4.2б).
Величину, обратную комплексному сопротивлению Z, называют комплексной проводимостью Y последовательной RLC-цепи, т.е.
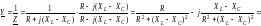
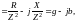
где
g
=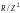 и
и
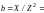
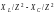 =
bL
bC
активная
и
реактивная
проводимости
цепи;
bL
=
=
bL
bC
активная
и
реактивная
проводимости
цепи;
bL
=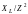 и
bC
=
и
bC
=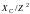
индуктивная
и ёмкостная
проводимости RLC-цепи.
индуктивная
и ёмкостная
проводимости RLC-цепи.
Итак, комплексная (полная) проводимость RLC-цепи
Y
= g
j(bL
bC)
= g
jb
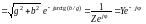 ,
,
где
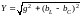 и
= arctg
и
= arctg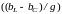
модуль
и
аргумент
комплексной проводимости цепи.
На рис. 4.2в
представлен
треугольник
проводимостей RLC-цепи
в комплексной плоскости.
модуль
и
аргумент
комплексной проводимости цепи.
На рис. 4.2в
представлен
треугольник
проводимостей RLC-цепи
в комплексной плоскости.
