1.1.3. Топологические параметры схем цепей. При анализе электрических схем пользуются следующими тополо­гическими параметрами схем:

 ветвь (В)  участок электрической цепи, вдоль которого протекает один и тот же электрический ток;

 узел (У)  место соединения ветвей электрической цепи. Обычно место, где соединены две ветви, называют не узлом, а соединением (или уст­ранимым узлом), а узел соединяет не менее трёх ветвей;

 контур  последовательность ветвей электрической цепи, образующая замкнутый путь, в которой один из узлов одновременно является началом и концом пути, а остальные встречаются только один раз. В элек­­трической цепи вы­де­ляют линейно не­зависимые контуры k_н, которые отличаются друг от друга хотя бы одной ветвью. Число независимых контуров зависит от числа ветвей В и числа уз­лов У в цепи:

k_н = В – (У – 1). (1.3)

Так, в схеме электрической цепи (рис. 1.1.1) ветвей В = 5, узлов У = 3, соединений 2, независимых контуров k_н = 3.

Примечания.

1. Точки 5, 6, 7 и 8 имеют одинаковый электрический по­тен­­ци­ал, поэтому они могут быть геометрически объединены в одну общую точку  узел.

2. Точки 1 и 4 соединяют по два элемента, поэтому их называют точ­ками соединений двух элементов, а не узлами.

1.1.4. Задача расчёта цепи. Расчёт электрической цепи заключается в опи­са­нии её схемы за­мещения математическими уравнениями и в решении си­стемы уравнений относительно электрических величин. Теория электрических и магнитных цепей базируется на введении па­раметров отдельных участков цепи, из которых основными являются сопро­тивления, индуктивности и ёмкости. Помимо этих параметров, вводят в рассмотрение еще множество других (например, маг­нитное сопротивление маг­нитной цепи, реактивные сопротивления и проводимости цепи переменного тока, и др.), находящихся в известной связи с ними или имеющих самостоятельное значение.

Задачей расчёта электрической цепи является, в первую очередь, оп­ре­де­ление токов и напряжений ветвей при заданных значениях параметров активных и пассивных элементов схемы цепи.

Для расчёта электрических цепей (точнее, их схем замещения) раз­работано несколько методов, наиболее общими из которых являются метод непосредственного применения законов Кирхгофа, ме­тод узловых напряжений, метод переменных состояния, метод контурных токов.

Примечание. Понятия «электрическая цепь» и «схема электрической цепи» часто отождествляют.

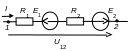
1.1.5. Законы Ома и Кирхгофа. Решение задач анализа электромаг­ни­т­ных процессов в известной схеме электрической цепи с заданными параметрами источников энергии и резистивных элементов базируется на применении закона Ома, первого и второго законов Кирхгофа, которые записывают соответственно для ветвей, узлов и контуров (табл. 1.1.3).

Закон Ома устанавливает зависимость между током и на­пря­жением на пассивной ветви при совпадении направлений тока и напряжения на ней (см. табл. 1.1.3, вторая строка). Для ветви с источниками напряжения используют обоб­щенный закон Ома: (см. табл. 1.1.3, третья строка). Знак «+» перед ЭДС E и напряжением U₁₂ записывают при совпадении их направлений с условно положительным направлением тока I и знак «-»  при не совпадении их направлений с направлением тока.

Первый закон Кирхгофа (1ЗК) записывают для узлов электрической схемы (см. табл. 1.1.3, четвертая строка). Закон формулируется следующим образом: алгебраическая сумма токов в любом узле схемы цепи равна нулю. При этом токи, направленные к узлу, при­­нято записывать со знаком «+», а уходящие от уз­ла, со знаком «-».

Второй закон Кирхгофа (2ЗК) применяется к контурам электрической цепи (см. табл. 1.1.3, пятая строка) и формулируется следующим образом: в лю­бом контуре схемы алгебраическая сумма ЭДС равна ал­ге­браической сум­ме напряжений на всех участках с сопротивлениями, входящими в этот контур. При этом ЭДС и напряжения на элементах контура за­писывают со знаком «+», если выбран­ное нап­равление обхода контура (например, по ходу часовой стрелки) совпадает с направлением напряжений (токов) на этих элементах, и со знаком «-» при их несовпадении.

Таблица 1.1.3. Топологические параметры схем цепей и их описание

Топологический параметр схемы	Участок схемы	Основание для составления уравнения	Выражение закона
Пассивная ветвь		Закон Ома
Ветвь с источниками напря­жения		Обобщенный закон Ома
Узел		Первый закон Кирхгофа (1ЗК)	Ik = 0, I1  J  I2  I3 = 0
Контур		Второй закон Кирхгофа (2ЗК)	Ek = Uk, E2  E3 = R1I1 + + R2I2  R3I3 U12

1.1.6. Метод расчёта, основанный на законах Кирхгофа. Анализ и расчёт лю­бой электрической цепи постоянного тока можно провести в результате совместного решения системы уравнений, составленных посредством первого и второго законов Кирхгофа. Число уравнений в системе равно числу ветвей в цепи (N_МЗК = В), при этом число независимых уравнений, которые можно запи­сать по 1ЗК, на од­но уравнение меньше числа узлов, т. е.

N_1ЗК = У  1, (1.4)

а число независи­мых уравнений, записываемых по 2ЗК,

N_2ЗК = B  (У  1), (1.5)

где В  число ветвей с неизвестными токами (без ветвей с источниками тока); У  чи­сло узлов.

Составим посредством законов Кирхгофа необходи­мое число уравнений для определения токов ветвей схемы (рис. 1.1.2), если заданы ЭДС E₁ и E₂ источников напряжения, ток J источника тока и соп­ротивления R₁,…, R₅ резисторов.

N_МЗК = N_1ЗК + N_2ЗК = В.

С этой целью:

1. Проведём топологический анализ схемы для определения числа независимых урав­­нений. В схеме B₁ = 6 вет­вей, У = 3 узла. Од­нако в ветви с ИТ ток J задан, поэтому число независимых ветвей В = 5. Число независимых урав­нений для решения задачи по методу законов Кирхгофа

N_МЗК = В = 5.

2 . Пронумеруем узлы и выберем произвольно направления токов в вет­вях (рис. 1.1.3).

3 . Составим уравнения по 1ЗК (N_1ЗК = У  1 = 3  1 = 2):

для узла 1: I₁  I₂  J  I₃ = 0, (1)

для узла 2: I₃  I₄ + I₅ = 0. (2)

4. Выберем независимые кон­ту­ры и направление обхода контуров, на­при­­мер, по ходу часовой стре­лки. В на­шем случае имеется три независимых контура, так как ветвь с заданным током J ИТ в уравнениях, составляемых по 2ЗК, не учитывается:

N_2ЗК = B  (У  1) = 5 – (3 – 1) = 3.

5. Составим три уравнения по 2ЗК:

для контура 1'-1-0-1': E₁ = R₁I₁ + R₂I₂, (3)

для контура 1-2-0-1: 0 = R₃I₃ + R₄I₄  R₂I₂, (4)

для контура 2-2'-0-2: E₂ = R₅I₅  R₄I₄ . (5)

6. Решив систему уравнений (1)…(5), например, методом Гаусса или с использованием формул Крамера, можно определить все неизвестные токи ветвей цепи.

1.1.7. Структурные преобразования схем замещения цепей. Расчёт элек­трических цепей можно упростить путём преобразования их схем замещения в более простые и удобные для расчёта. Такие преобразования приводят, как пра­вило, к уменьшению числа узлов схемы и, следовательно, необходимого числа исходных уравнений для расчёта.

Так, ветвь с последовательно соединёнными резисторами R₁, R₂, … , R_n может быть преобразована в простую схему с одним резистивным эле­ментом (рис. 1.1.4а), эквивалентное сопротивление которого равно сумме сопротивлений:

(1.6)

а ветвь с несколькими последовательно соединёнными источниками напряжения и резисторами (рис. 1.1.4б) также может быть преобра­зована в ветвь с одним эквивалентным ИН с параметрами R_э и Е_э (рис. 1.1.4в):

и (1.7)

П 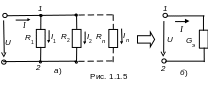араллельно соединённые резисторы с сопротивлениями R₁, R₂,…, R_n (рис. 1.1.5а) можно заменить одним резистором с проводимостью G_э (рис. 1.1.5б).

Так как напряжение на всех ветвях одно и тоже, равное U, то токи ветвей

где ,  проводимости ветвей в сименсах.

В схеме с двумя узлами 1 и 2 (см. рис. 1.1.5а) ток на входе цепи

а эквивалентная про­водимость и эквивалентное сопротивление пассивного участка цепи между узлами 1 и 2 равны

и . (1.8)

Э лектрические схемы, имеющие сочетание последовательного и параллельного соединений участков цепи (смешанное соединение), могут быть преобразованы в более простые эквивалентные схемы путём замены параллельных ветвей одной ветвью, а последовательно соединённые участки цепи – одним участком. Так, например, для схемы рис. 1.1.6а вначале нужно найти эквивалентное сопротивление параллельного участка 23 с тремя параллельно включенными резисторами

, (1.9)

а затем сложить его с сопротивлением R₁ (рис. 1.1.6б, в):

В электрических цепях элементы могут быть соединены по схеме треугольник или по схеме звезда (рис. 1.1.7).Треугольником называют соединение трёх элементов, в котором конец первого элемента со­еди­нён с началом вто­рого, конец второго с началом третьего, а конец тре­тьего с началом первого (рис. 1.1.7а). Звездой называют соединение, в котором кон­­цы трёх элементов со­единены в одну общую точ­ку п (рис. 1.1.7б).

С целью уменьшения числа узлов в схеме цепи, соединения элементов треугольником преобразуют в эквивалентное соединение звездой посредством сле­­­ду­ющих формул:

, , (1.10)

т.е. сопротивление луча эквивалентной звезды равно дроби, в числителе которой произведение двух сопротивлений сторон треугольника, примыкающих к рассматриваемому узлу, делённому на сумму всех сопротивлений сторон треугольника.

1.1.8. Правило делителя напряжения. В ветви, состоящей их двух после­дова­те­льно соединённых резисторов (рис. 1.1.8а), напряжение на одном из резисторов равно при­ложенному к ветви напряжению, умноженному на сопротивление данного резистора и делённому на сумму сопротивлений обоих резисторов, т.е.

и (1.11)

1.1.9. Правило делителя тока. Для цепи с двумя параллельно соеди­нёнными резисторами (рис. 1.1.8б) ток одной из двух параллельных ветвей цепи равен подходящему к разветвлению току I, ум­ноженному на сопро­тивление другой (противоположной) ве­тви и делён­ному на сумму соп­ротивлений обеих ветвей, т.е.

и (1.12)

1.1.10. Метод узловых напряжений. Метод узловых напряжений (МУН) базируется на первом законе Кирхгофа и обобщенном законе Ома. В нём за вспомогательные расчётные величины принимают так называемые узловые напряжения U₁₃  напряжения между каждым k-м узлом схемы и выбранным базисным узлом (его будем обозначать цифрой 0), потенциал которого принимают равным нулю. Число уравнений для расчёта схемы по МУН

N_МУН = У  1. (1.13)

Для каждого узла, кроме базисного, составляют уравнение по 1ЗК. В полученных уравнениях токи ветвей, присоединённых к базисному узлу, выражают через узловые напряжения и проводимости посредством обобщённого закона Ома:

(1.14)

где G₁₃ = 1/R_k  проводимость k-й ветви.

Ток в ветви, подключённой к узлам k и j,

= (E_kj  U_k0 + U_j0)G_kj, (1.15)

где U_kj = U_k0  U_j0 – межузловое напряжение; G_kj = 1/R_kj  меж­узловая про­водимость.

После группирования членов при соответствующих узловых напряжениях и переноса E_kG_k и токов J_k источников тока в правую часть, получают систему уравнений относительно неизвестных узловых напряжений.

Структура каждого уравнения одинаковая, например, уравнение относительно узла 1:

G₁₁U₁₀  G₁₂U₂₀  ...  G_1nU_n0 = + (1.16)

где G₁₁ = G₁ + G₂ + ... + G_n  собственная проводимость узла 1, равная сумме проводимостей ветвей, присоединённых к узлу 1 (проводимости ветвей с ИТ не учитываются, так как G_j = 1/R_j = 0 (R_j = )); G₁₂, ..., G_1n – меж­узловые проводимости; +  узловой ток узла 1;  алгебраическая сумма произведений ЭДС ветвей, присоединённых к узлу 1, на проводимости этих ветвей, причём со знаком «+» («-») записывают произведения, если ЭДС направлена к узлу 1 (от узла 1);  алгебраическая сумма токов источников тока ветвей, подключённых к узлу 1, при­чём токи J_k записывают со знаком «+» («-»), если они направлены к узлу 1 (от узла 1).

Решив систему уравнений относительно узловых напряжений, определяют межузловые напряжения и токи ветвей посредством соотношений (1.14) и (1.15).

Пример 1.1.1. Пользуясь методом узловых напряжений, определить токи ветвей схе­мы (рис. 1.1.9), если E₁ = 12 В, E₅ = 15 В, J = 2 А, R₁ = 1 Ом, R₂ = 5 Ом, R₃ = = R₄ = 10 Ом, R₅ = 1 Ом. В схеме 6 ветвей и 3 узла.

Р ешение. 1. Выбираем базисный узел 0 и направления узловых напряжений U₁₀ и U₂₀ от узлов 1 и 2 к базисному (см. рис. 1.1.9).

2. Составляем (N_МУН = У  1 = 3  1 = 2) уравнения по МУН:

для узла 1: G₁₁U₁₀  G₁₂U₂₀ = E₁G₁  J,

для узла 2: G₂₁U₁₀ + G₂₂U₂₀ = E₅G₅,

где G₁₁ = G₁ + G₂ + G₃, G₁₂ = G₃ = 1/R₃, G₂₂ = G₃ + G₄ + G₅, G₂₁ = G₁₂ = G₃.

3. После подстановки числовых значений (G₁ = 1/R₁ = 1 См, G₂ = 0,2 См, G₃ = = G₄ = 0,1 См, G₅ = 1 См) имеем:

1,3U₁₀  0,1U₂₀ = 12  2 = 10,

 0,1U₁₀ + 1,2U₂₀ = 15.

4. Воспользовавшись форму­­лами Крамера, находим узловые нап­ря­жения:

Примечание. Вычисление узловых напряжений нужно проводить с большой точностью. В данном примере достаточно округлить четвёртый знак после запятой.

5. Межузловое напряжение

U₁₂ = U₁₀  U₂₀ = 8,7097  13,226 =  4,5163 B.

6. Искомые токи ветвей (см. выбранные направления токов ветвей на рис. 1.1.9):

I₁ = (E₁  U₁₀)G₁ = 3,29 A, I₂ = U₁₀G₂ = 1,754 A,

I₃ = U₁₂G₃ =  0,452 A, I₄ = U₂₀G₄ = 1,323 A,

I₅ = (E₅ + U₂₀)G₅ = 1,774 A.

7. Проверим результаты расчёта токов. Согласно 1ЗК для узла 2:

= I₃  I₄  I₅ =  0,452  1,323 + 1,774 = 0.

1.1.11. Метод двух узлов. Метод двух узлов является частным случаем метода узловых напряжений и применяется для расчёта схем, содержащих (после преобразования) два узла и произвольное число параллельных пассивных и активных ветвей. Для расчёта токов ветвей цепи составляют и решают одно уравнение узлового напряжения , равное алгебраической сумме токов, создаваемых всеми источниками напряжения и источниками тока цепи, делённой на собственную проводимость узла , т.е.

(1.17)

а токи ветвей определяют по обобщённому закону Ома (см. (1.14)).

Пример 1.1.2. Упростить схему цепи (рис. 1.1.10а) посредством преобразования пас­сивного треугольника в эквивалентную звезду и найти токи в преобразованной схеме методом двух узлов. Токи ветвей пассивного треугольника исходной схемы найти из составленных уравнений 1ЗК для узлов треугольника и (при необходимости) уравнения 2ЗК для контура, в который входит одна из ветвей треугольника с искомым током. Параметры схемы замещения цепи: E₅ = 20 В, E₆ = 36 В; R₁ = 10 Ом, R₂ = 12 Ом, R₃ = 4 Ом, R₄ = 8 Ом, R₅ = 6 Ом, R₆ = 5 Ом.

Решение. 1. Обозначим узлы и пунктирными линиями лучи (ветви) эквивалентной звезды R_1n, R_2n, R_3n (рис. 1.1.10б), равные (см. (1.10))

2 . В результате преобразований получили схему с двумя узлами: n и 4 (рис. 1.1.11), в которой узлы исходной схемы 1, 2 и 3 стали соединениями.

3 . Расчет схемы (рис. 1.1.11) методом двух узлом проведем в три этапа:

а) выбираем базисный узел 4 и приравниваем его потенциал к нулю (₄ = 0);

б) направим узловое напряжение U_n4 от узла n к узлу 4 и найдем его значение (см. (1.1.11):

где

 собственная проводимость узла п;

в) токи ветвей определим по обобщенному закону Ома:

I₆ = (-E₆ + U_n4)G_1n6 = (36 + 8,189)  0,153 =  4,26 А,

I₄ = U_п4G_2n4 = 8,189  0,0793 = 0,65 A,

I₅ = (E₅ + U_n4)G₂ = (20 + 8,189)  0,128 = 3,61 A.

4. Определим токи сторон (ветвей) пассивного треугольника исходной схемы. С этой целью выберем условно положительные направления токов I₁, I₂ и I₃ (рис. 1.1.12) и составим уравнение 2ЗК для наружного контура:

E₆ = -R₆I₆ – R₁I₁ + R₄I₄.

Откуда ток

I₁ = (-E₆ - R₆I₆ + R₄I₄)/R₁ = (-36 + 5  4,26 + 8  0,65)/10 = - 0,95 A.

Из уравнения 1ЗК для узла 2 (см. рис. 1.1.12) I₁ + I₂ + I₄ = 0 находим ток

I₂ = - I₁ - I₄ = 0,95 – 0,65 = 0,3 А,

а из уравнения 1ЗК I₂ + I₃ – I₅ = 0 для узла 3 – ток

I₃ = -I₂ + I₅ = -0,3 + 3,61 = 3,31 А.

5. Проверим результаты расчета токов схемы цепи двумя методами:

 посредством проверки выполнения условия баланса мощностей в цепи и

 посредством схождения потенциальной диаграммы, построенной для замкнутого контура схемы цепи.

а) Условие баланса мощностей в электрической цепи. Из закона сохранения энергии следует, что сумма мощностей, отдаваемой всеми источниками энергии цепи, должна быть равна сумме мощностей, потребляемой всеми приёмниками энергии. Необходимо иметь в виду, что потребляется и отдается не мощность, а энергия в джоулях. Итак, мощность (секундная энергия), развиваемая источниками энергии в схеме цепи, дол­жна быть равна сумме мощностей резисторов схемы, т.е.

= . (1.18)

При этом произведение ЭДС источника энергии Е_k и протекающего через него тока I_k записывается в сумме слева (см. (1.18)) со знаком «+», если их направления совпадают, и со знаком «-», если они имеют противоположное направление. В последнем случае источник является приемником электрической энергии.

Для схемы цепи (рис. 1.1.12)

Е₅I₅  Е₆I₆ = 20  3,61 + 36  4,26 =

= 10  0,95² + 12  0,3² + 4  3,31² + 8  0,65² + 6  3,61² + 5  4,26² = 72,2 + 153,36 =

= 9,025 + 1,08 + 43,82 + 3,38 + 78,19 + 90,74 = 225,56  226,24 Вт.

Таким образом, условие баланса мощностей выполняется.

б) Построение потенциальной диаграммы для контура. Перед построением потенциальной диаграммы (R) выбранного контура необходимо нарисовать его схему и указать истинные (а не первоначальные условно положительные направления токов ветвей), обозначения всех узлов и точек соединений, обозначение заземленного узла, указать направление обхода контура, и только после этого провести расчёт потенциалов узлов (целесообразно и точек соединений), затем выбрать мас­штаб сопротивлений резисторов, отложив их друг за другом от 0 (по направлению обхода контура) на оси абсцисс графика, далее, выбрать масштаб для потенциалов узлов и соединений на оси ординат, и выполнить построение графика, указав у вершин изломов графика потенциалы _k соответствующих узлов и соединений.

Пример 1.1.3. Построить потенциальную диаграмму  = f(R) для контура 1-3-4-1 схемы цепи (см. рис. 1.1.12) с параметрами: Е₅ = 20 В, Е₆ = 36 В, R₃ = 4 Ом, R₅ = 6 Ом, R₆ = 5 Ом, I₃ = 3,31 А, I₅ = 3,61 А, I₆ = 4,26 А.

Решение. 1. Вычерчиваем выбранный контур с указанием истинных направлений токов в ветвях (рис. 1.1.13а). Произвольно выбираем узел контура, например, узел 1, заземляем его, т.е. считаем, что потенциал ₁ = 0.

2. Отложив последовательно значения сопротивлений резисторов по оси R (мас­штаб 2 Ом в 1 см) (рис. 1.1.13б) в соответствии с выбранным обходом контура (по ходу часовой стрелки), определяем потенциал точки 3:

₃ = ₁ – R₃I₃ = 0 – 4  3.31 = -13,24 B.

П адение напряжения R₃I₃ взято со знаком минус, так как ток I₃ (по определению) протекает от узла 1 с бóль­шим потенциалом к узлу 3 с меньшим потенциалом (₃ < ₁).

3. Вычислим потенциал точки соединения 3:

_3 = ₃ + E₅ = -13,24 + 20 = 6,76 В.

ЭДС E₅ взята со знаком плюс, так как она (по определению) действует от узла 3 с меньшим потенциалом к точке соединения 3 с бóльшим потенциалом. При переходе от узла 3 к точке соединения 3 потенциал изменяется скачком.

4. Потенциал точки 4

₄ = _3 – R₄I₄ = 6,76 – 6  3,61 = - 14,9 В.

Напряжение R₄I₄ взято со знаком минус, так как ток I₅ протекает от точки соединения 3 с бóль­шим потенциалом к узлу 4 с меньшим потенциалом (₄ < _3).

5. По аналогии (с учётом указан­ного принципа действия ЭДС и про­те­ка­ния токов) запишем потенци­алы точки соединения 5 и узла 1:

₅ = ₄ + E₆ = - 14,9 + 36 = 21,1 B (ЭДС E₆ взята со знаком плюс, так как ₅ > ₄ );

₁ = ₅ – R₆I₆ = 21,1 – 5  4,65 = 21,1 – 21,3  0 (ток I₆ протекает от точки 5 к узлу 1, поэтому потенциал ₅ > ₁ = 0).

Результаты расчёта подтверждают правильность расчета токов в ветвях схемы.

6. После переноса из левых частей уравнений потенциалов точек контура схемы вправо и сложения правых частей уравнений получим выражение 2ЗК для анализируемого контура, т.е.

E₅ + E₆ = R₃I₃ + R₅I₅ + R₆I₆.= 20 + 36 = 13,24 + 21,66 + 21,3 = 56  56,2 В.

7. Выбираем масштаб для потенциалов по оси  (10 В в 1 см) и строим потенциальную диаграмму (см. рис. 1.1.13б).

2.1.12. Метод эквивалентного генератора. Метод эквивалентного генератора (МЭГ) основан на теореме об эквивалентном генераторе, в которой сложную схему электрической цепи с произвольным числом ИН и ИТ рассматривают как активный двухполюсник (рис. П1.14) по отношению к зажимам 1 и 2 ветви с искомым током

(1.19)

где E_эг = U_12(х)  ЭДС эквивален­тного генератора, рав­­­ная напряжению холостого хода U_12(х) между зажимами 1 и 2 при отклю­чён­ном пассивном элементе ветви с сопро­ти­влением R₂; R_эг  внутреннее сопротивление эквивалентного генератора, равное входному сопро­тив­лению цепи относительно разомкнутых зажимов 1 и 2 (при этом в цепи все идеальные ИН замыкают накоротко (но их внутренние сопротивления оставляют в схеме), а ветви с ИТ  размыкают).

П ример 1.1.4. Определить ток I₂ (см. рис. 1.1.12) методом эквивалентного генератора и сравнить его значение со значением, найденным в примере 1.1.2.

Р ешение 1. Разорвем ветвь с резистором R₂ и определим напряжение холостого хода между узлами 2 и 3, т. е. U_23(х) = E_эг = R₁I_1(х) + R₃I_3(х) (рис. 1.1.15а). Токи I_1(х) и I_3(х) найдем, записав уравнения законов Кирхгофа.

В схеме (рис. 1.1.15а) три ветви и два узла 1 и 4. Необходимо составить три уравнения: одно по 1ЗК и два по 2ЗК:

I_1(х)  I_3(х)  I_6(х) = 0 (1ЗК для узла 1), (1)

(R₁ + R₄)I_1(х) + (R₃ + R₅)I_3(х) + 0I_6(х) = E₅ (2ЗК для верхнего контура), (2)

0I_1(х) + (R₃ + R₅)I_3(х) – R₆I_6(х) = E₅ + E₆ (2ЗК ля нижнего контура). (3)

I_1(х)  I_3(х)  I_6(х) = 0,

18I_1(х) + 10I_3(х) + 0I_6(х) = 20,

0I_1(х) + 10I_3(х)  5I_6(х) = 56.

Воспользуемся программой ElCalc (электротехнический калькулятор), записанной на компакт-диске [2], для вычисления токов I_1(х), I_3(х) и I_6(х) системы (1)…(3) (рис. 1.1.16). Итак, имеем: I_1(х) = -0,8125 А, I_3(х) = 3,4625 А, I_6(х) = -4,275 А.

ЭДС эквивалентного генератора

E_эг = U_23(х) = R₁I_1(х) + R₃I_3(х) = -100,8125 + 43,4625 = -8,125 + 13,85 = 5,725 В.

2. Чтобы найти внутреннее сопротивление эквивалентного генератора R_ЭГ = R₂₃ (рис. 1.1.15б), заменим треугольник со сторонами R₁, R₄ и R₆ эквивалентной звездой с лучами R₁₄, R₁₆ и R₄₆ (рис.. 1.1.15в), равными

Т огда внутренне сопротивление эквивалентного генератора (см. 1.1.15в)

R_ЭГ = R₂₃ = R₂₄ +

Ом.

3. Искомый ток

А.

Значения тока I₂, полученные при расчете двумя методами, практически идентичны, что подтверждает правильность его расчета._.

П р и м е ч а н и е. Напряжение U_23(х) = E_эг = R₁I_1(х) + R₃I_3(х) можно найти, составив два уравнения по методу контурных токов, или методом двух узлов, заземлив узел 1 (или 4) и определив узловое напряжение U₄₁ (или U₁₄), а затем токи I_1(х) и I_3(х) по обобщенному закону Ома.