
- •Введение
- •1. Матрицы и действия с матрицами
- •2. Определители
- •3. Обратная матрица. Решение матричных уравнений
- •4. Ранг матрицы
- •5. Системы линейных уравнений. Основные понятия
- •6. Решение линейных систем по формулам Крамера
- •7. Решение систем с помощью обратной матрицы
- •8. Исследование систем линейных уравнений. Метод Гаусса
- •9. Однородные системы
- •10. Собственные значения и собственные векторы матрицы
- •Индивидуальное задание
- •Приложение
- •Литература
3. Обратная матрица. Решение матричных уравнений
Матрица
![]() называется
обратной
к квадратной матрице
,
если
называется
обратной
к квадратной матрице
,
если
![]() ,
,
где - единичная матрица, имеющая тот же порядок, что и матрица .
Обратная матрица
существует только в том случае, если
![]() ,
и ее элементы находятся по формуле
,
и ее элементы находятся по формуле
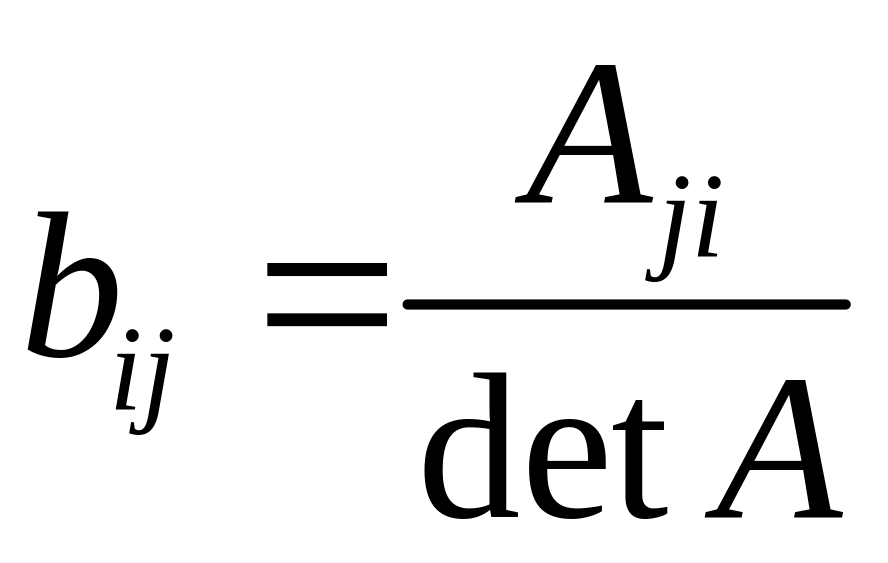 ,
,
где
![]() - алгебраическое дополнение к элементу
- алгебраическое дополнение к элементу
![]() .
.
Внимание! Алгебраические дополнения, которые вычисляются к элементам строки, записываются в столбец.
Если
![]() ,
то матрица
,
то матрица
![]() называется вырожденной,
в противном случае невырожденной,
т.е. обратная матрица существует только
для невырожденных матриц.
называется вырожденной,
в противном случае невырожденной,
т.е. обратная матрица существует только
для невырожденных матриц.
Обозначается
обратная матрица
![]() ,
т.е.
,
т.е.
![]() ,
,
при этом ее
определитель
 .
.
Для невырожденных матриц и выполнены соотношения
![]() ,
,
![]() .
.
Введение обратной матрицы позволяет решать матричные уравнения. В конечном счете, матричные уравнения сводятся к двум простейшим уравнениям:
![]() или
или
![]() .
.
Если матрица - квадратная, невырожденная, то эти уравнения имеют единственное решение, которое можно получить с помощью обратной матрицы. Так как при умножении матриц коммутативный закон не выполняется, они решаются разными способами.
При поиске решения первое из уравнений надо умножать на обратную матрицу слева, а второе справа, т.е.
![]() ,
(5)
,
(5)
![]() .
(6)
.
(6)
►Пример 5. Найти
решение матричного уравнения
,
то есть определить матрицу
![]() ,
если
,
если
 ;
;
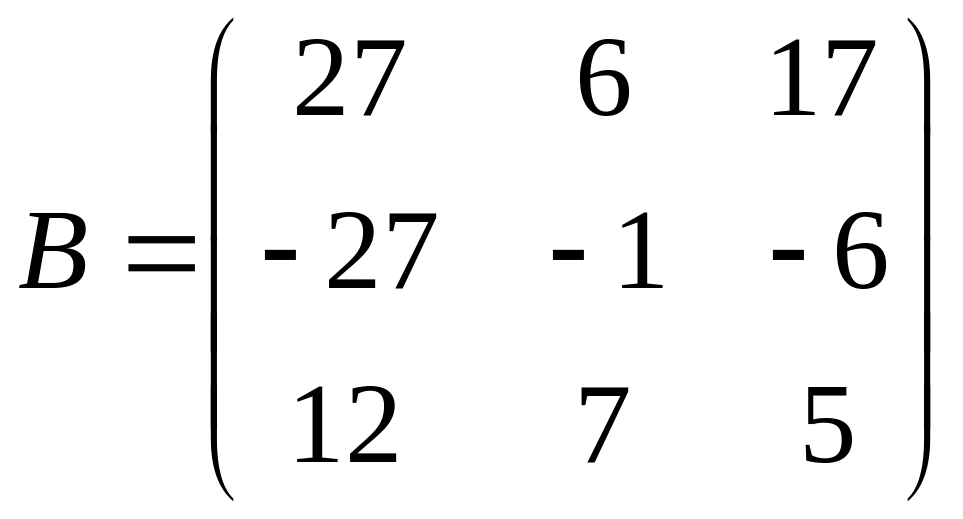 .
.
Решение.
Решение в матричном
виде определяется формулой (5), т.е.
![]() ,
если матрица
невырожденная. Вычислим определитель
матрицы
:
,
если матрица
невырожденная. Вычислим определитель
матрицы
:
 .
.
Следовательно, матрица невырожденная, и для нее существует обратная матрица. Проведем вычисления, необходимые для построения обратной матрицы. Вычислим алгебраические дополнения:

Составим обратную
матрицу
![]() и
найдем неизвестную матрицу
и
найдем неизвестную матрицу![]() .
.
 ,
,
При вычислениях
множитель
 рекомендуем оставлять перед матрицей
и проводить умножение полученной матрицы
на него на последнем этапе вычислений.
рекомендуем оставлять перед матрицей
и проводить умножение полученной матрицы
на него на последнем этапе вычислений.
►Пример 6.
Найти решение матричного уравнения
,
если
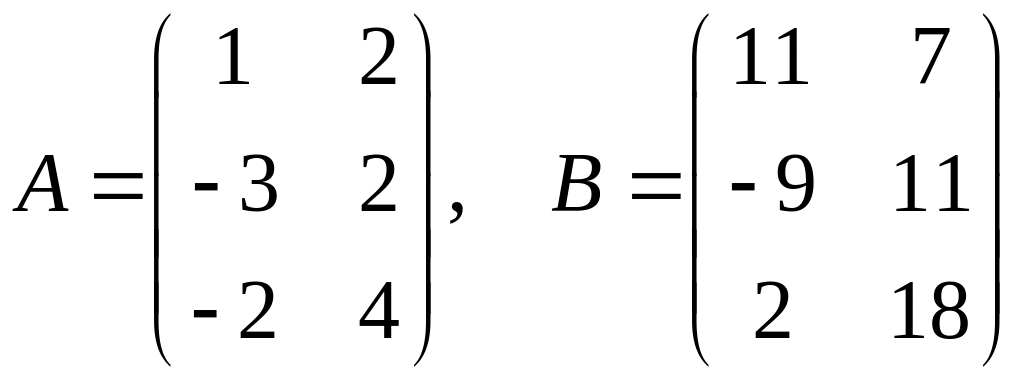 .
.
Решение.
Формулой (5)
воспользоваться нельзя, так как матрица
не квадратная, следовательно, для нее
не существует обратной матрицы. Умножим
обе части уравнения на транспонированную
матрицу
![]() слева,
получаем
слева,
получаем
![]() .
.
Матрица
![]() − квадратная и, если ее определитель
не равен нулю, то решение заданного
уравнения имеет вид
− квадратная и, если ее определитель
не равен нулю, то решение заданного
уравнения имеет вид
![]() .
.
Проведем вычисления:
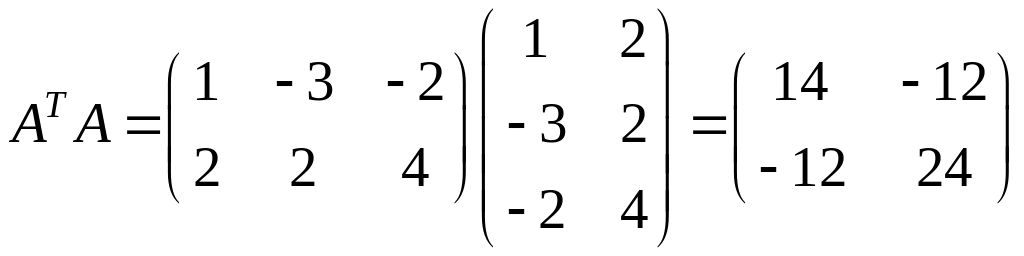 .
.
Определитель
полученной матрицы
![]() .
Следовательно, обратная матрица к
матрице
существует, и можно найти матрицу
:.
.
Следовательно, обратная матрица к
матрице
существует, и можно найти матрицу
:.
 ,
,
 ,
,
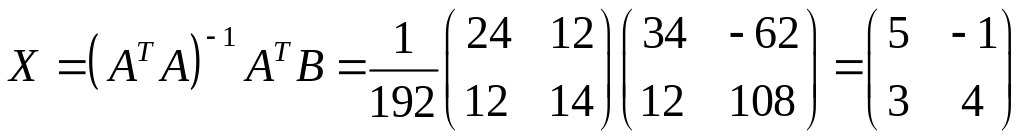 .
◄
.
◄
Упражнения.
1. Для заданных матриц найти обратную матрицу:
а)
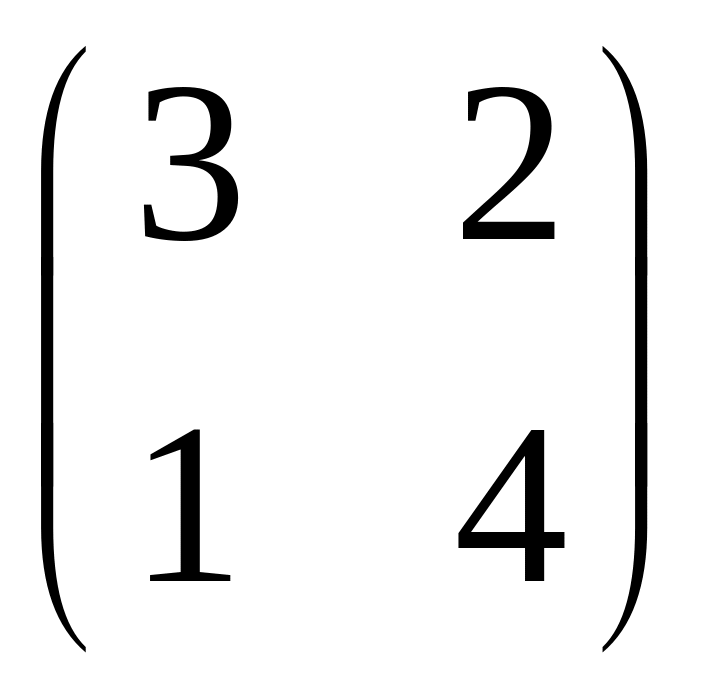 ;
б)
;
б)
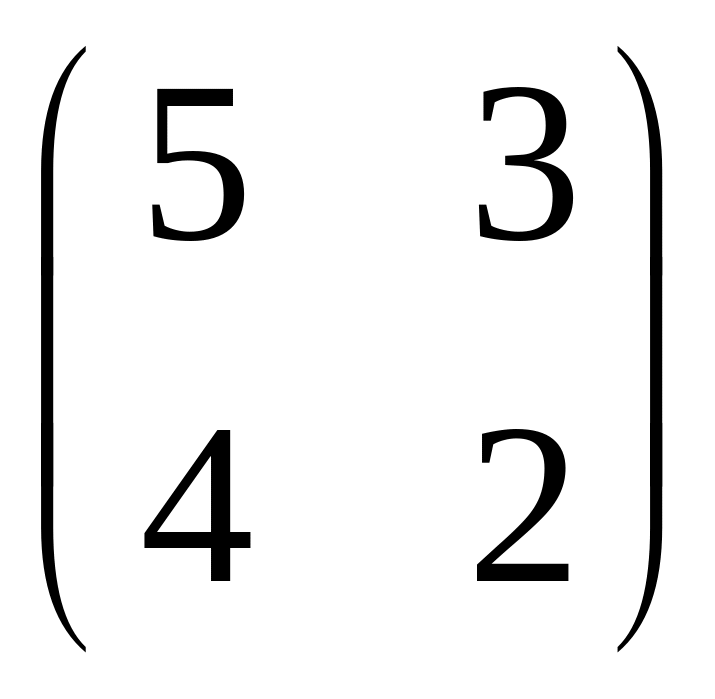 ;
в)
;
в)
 ;
г)
;
г)
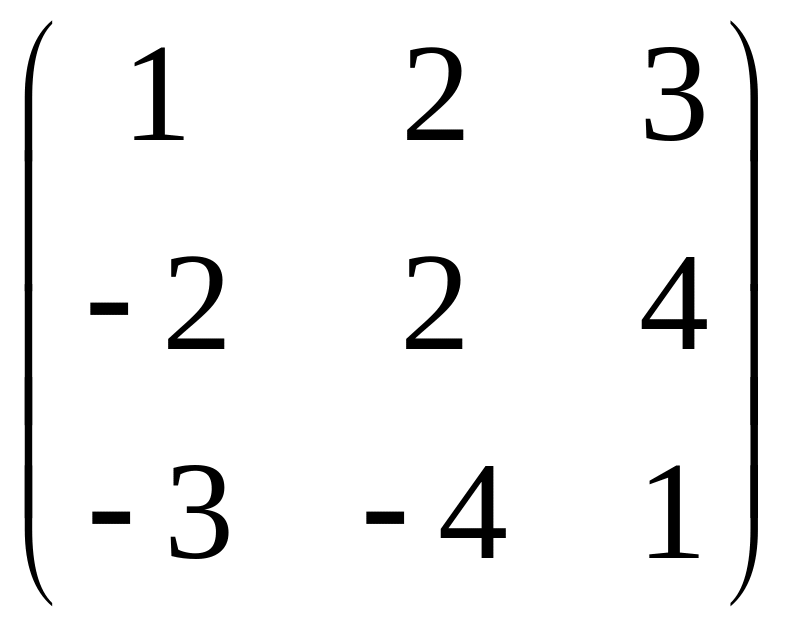 ;
д)
;
д)
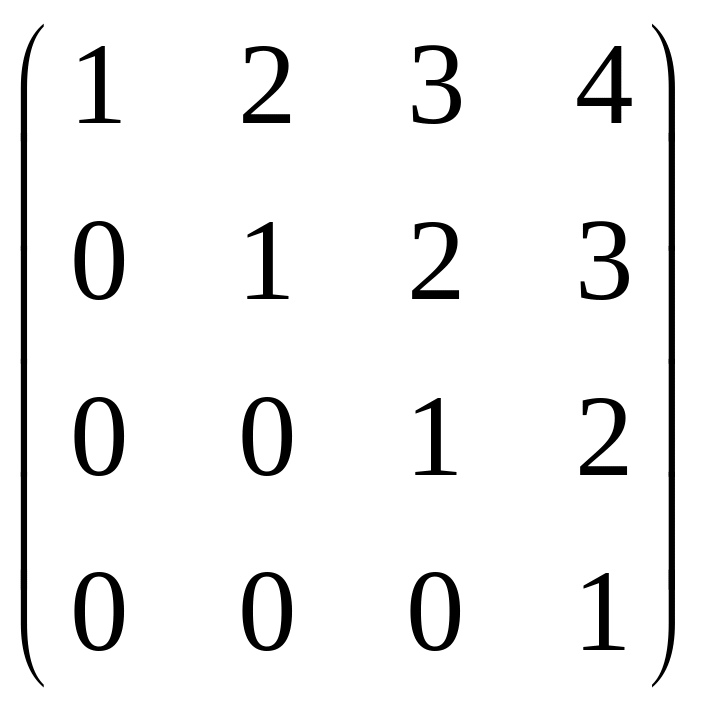 .
.
Ответы:
а)
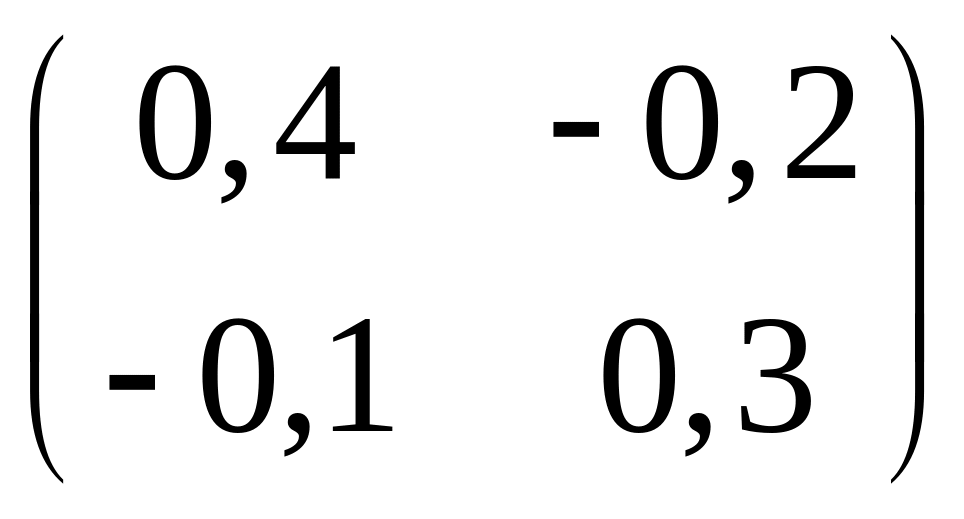 ;
б)
;
б)
 ;
в)
;
в)
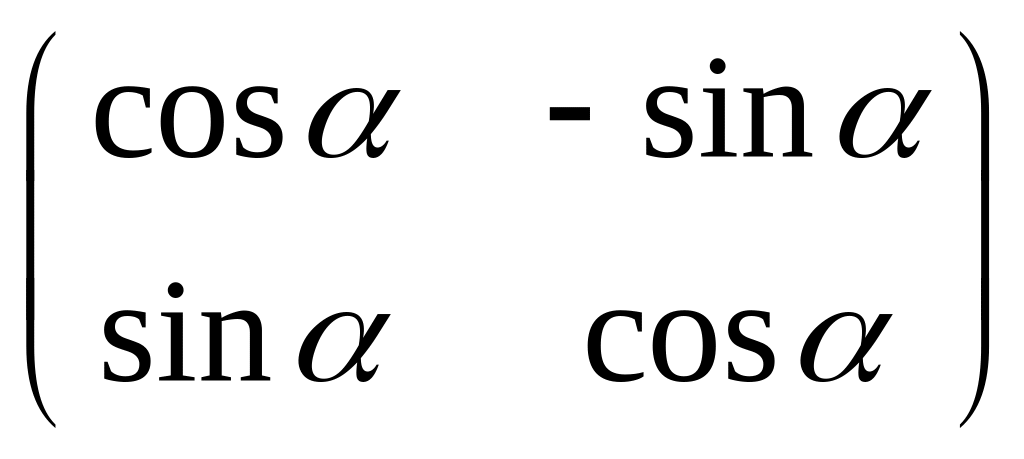 ;
;
г)
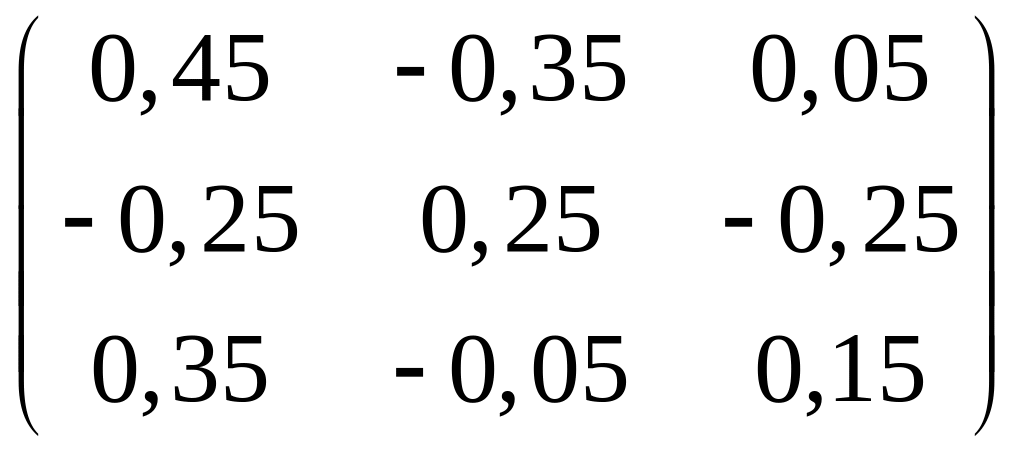 ;
д)
;
д)
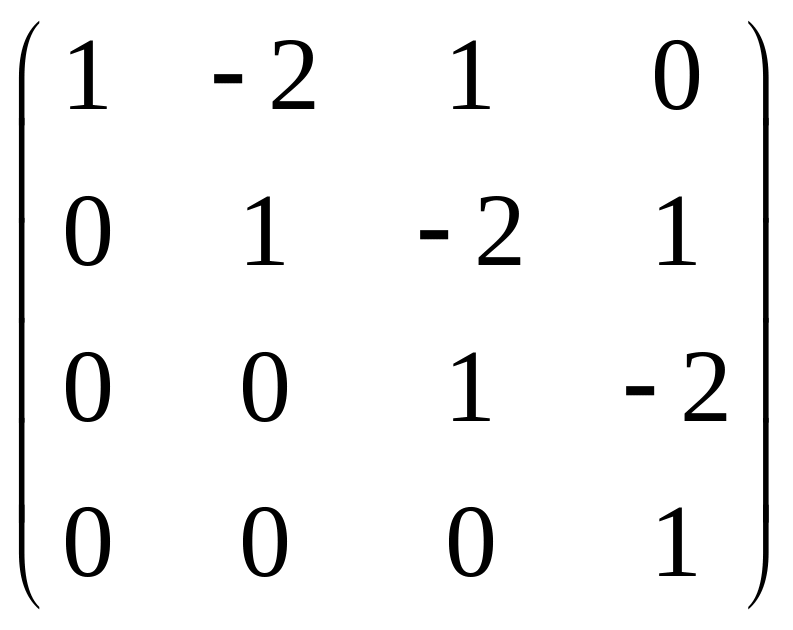 .
.
2. Найти неизвестную матрицу из уравнений:
а)
 ;
б)
;
б)
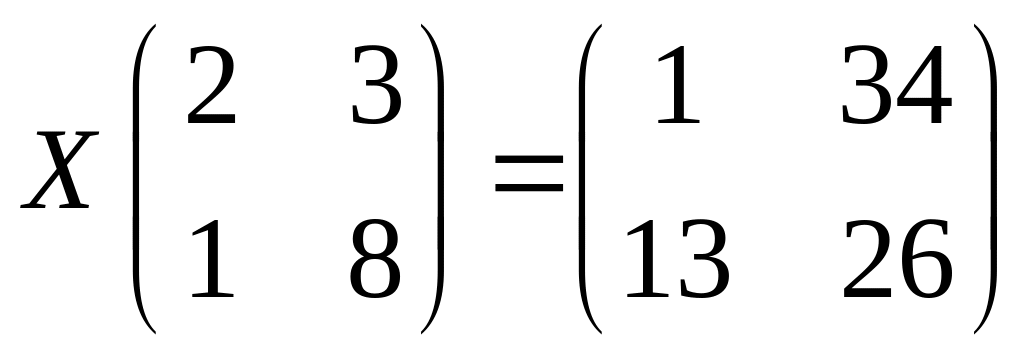 ;
;
в)
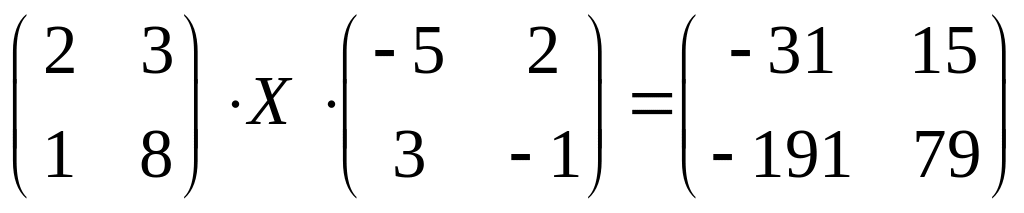 ;
;
г)
 ;
д)
;
д)
 .
.
Ответы:
а)
 ;
б)
;
в)
;
г)
;
б)
;
в)
;
г)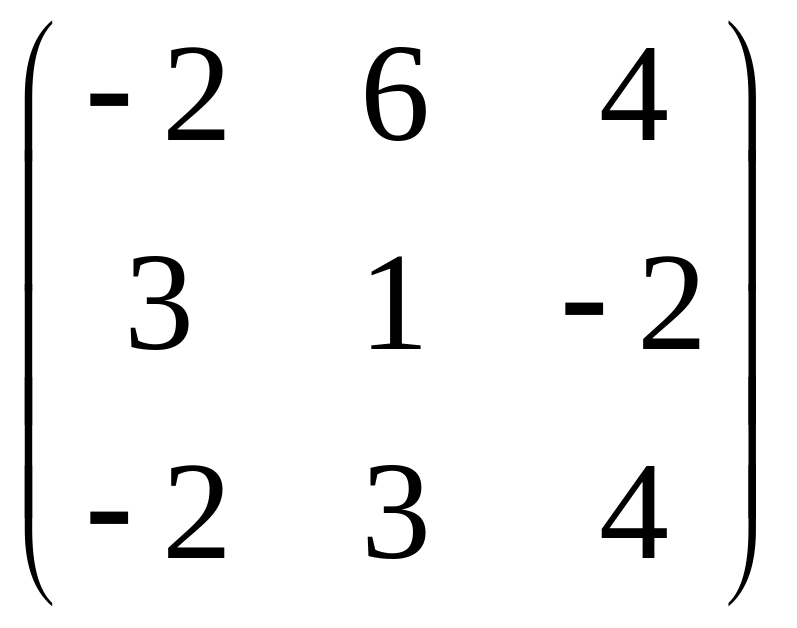 ;
д)
.
;
д)
.
