
какая-то теория / операции над графами
.pdf
ДИСКРЕТНАЯ МАТЕМАТИКА
ГРУППЫ 1/42, 1/147, 1/184
Ксенофонтова Ольга Леонидовна

ТЕОРИЯ ГРАФОВ
Операции над графами
практическое занятие
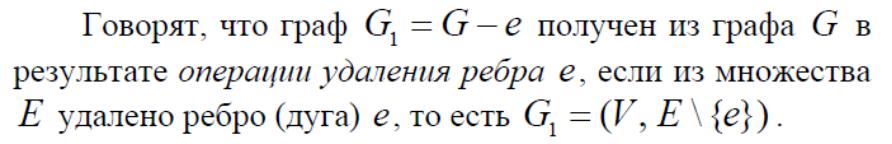
1. Операция удаления ребра
Пусть дан граф G=(V,E) и e E− его некоторое ребро (дуга).
Замечание 1. При удалении ребра e концы ребра не удаляются из множества V .
Замечание 2. Если выполняются подряд несколько операций удаления ребра, то результат не зависит от порядка, в котором эти ребра удаляются из графа.
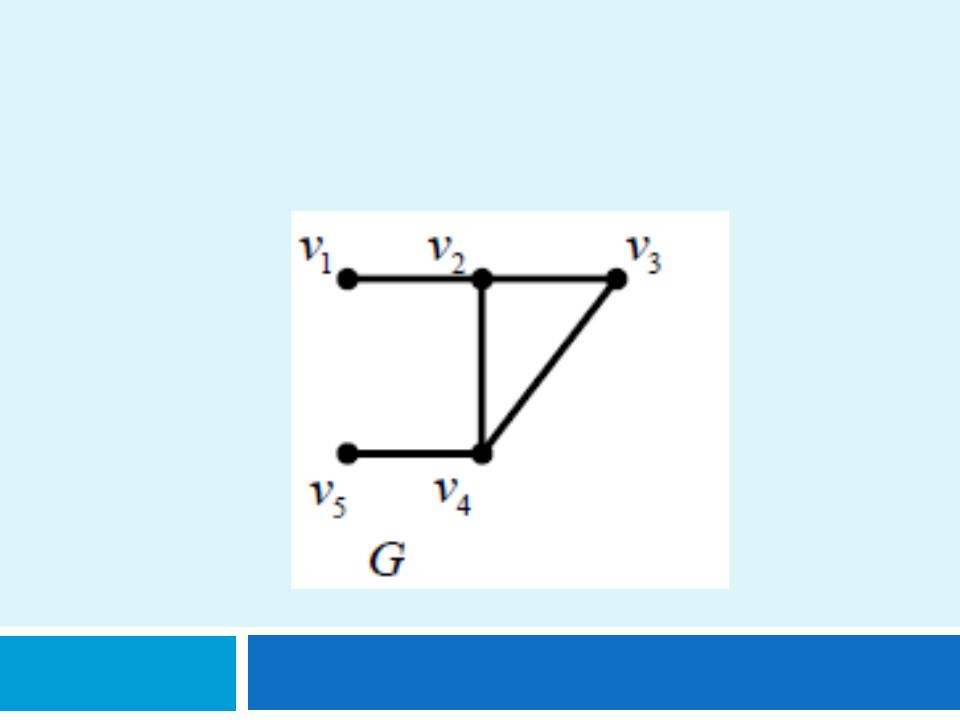
Задача 1.
Пусть дан граф G=(V,E). Выполнить над графом операции удаления ребер <v3, v4> и <v1, v2> .
е2
е1
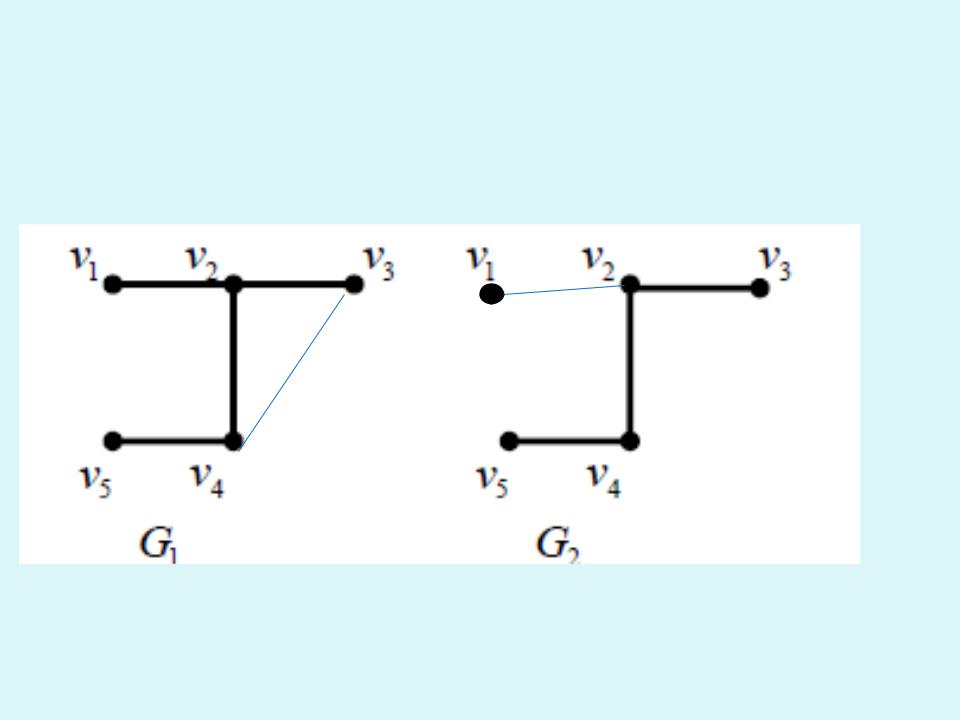
Задача 1.
Пусть дан граф G=(V,E). Выполнить над графом операции удаления ребер <v3, v4> и <v1, v2> .
Решение.
Удалили ребро е1 |
Удалили ребро е2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
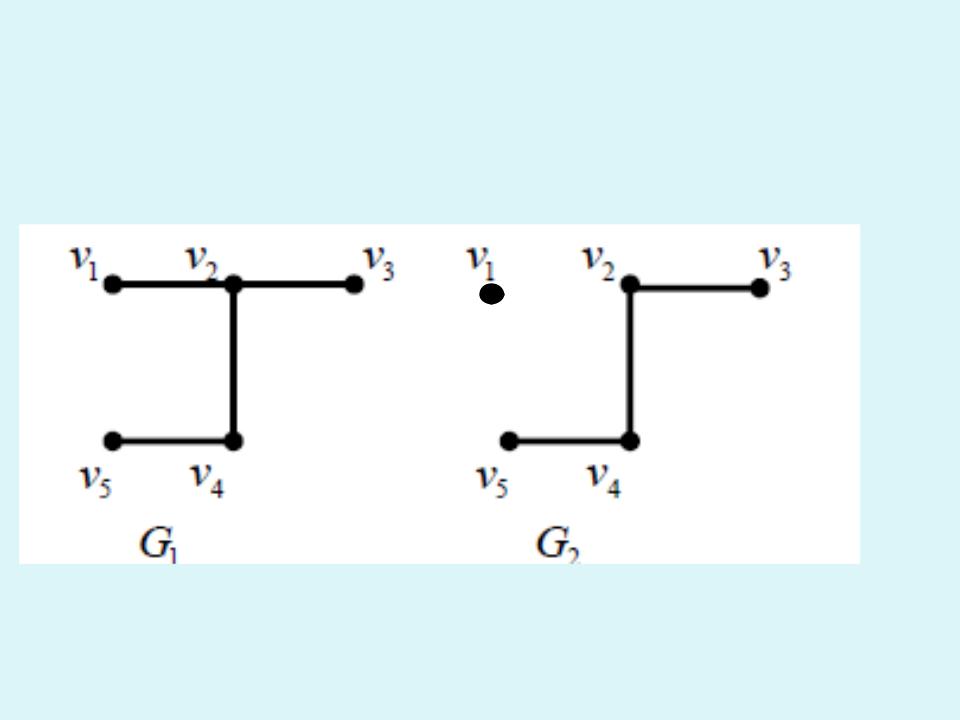
Задача 1.
Пусть дан граф G=(V,E). Выполнить над графом операции удаления ребер <v3, v4> и <v1, v2> .
Решение.
Удалили ребро е1 |
Удалили ребро е2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

2. Операция удаления вершины
Пусть дан граф G=(V,E) и v V− его некоторая вершина
Замечание 3. Если выполняются подряд несколько операций удаления вершины, то результат не зависит от порядка, в котором удаляются вершины из графа.
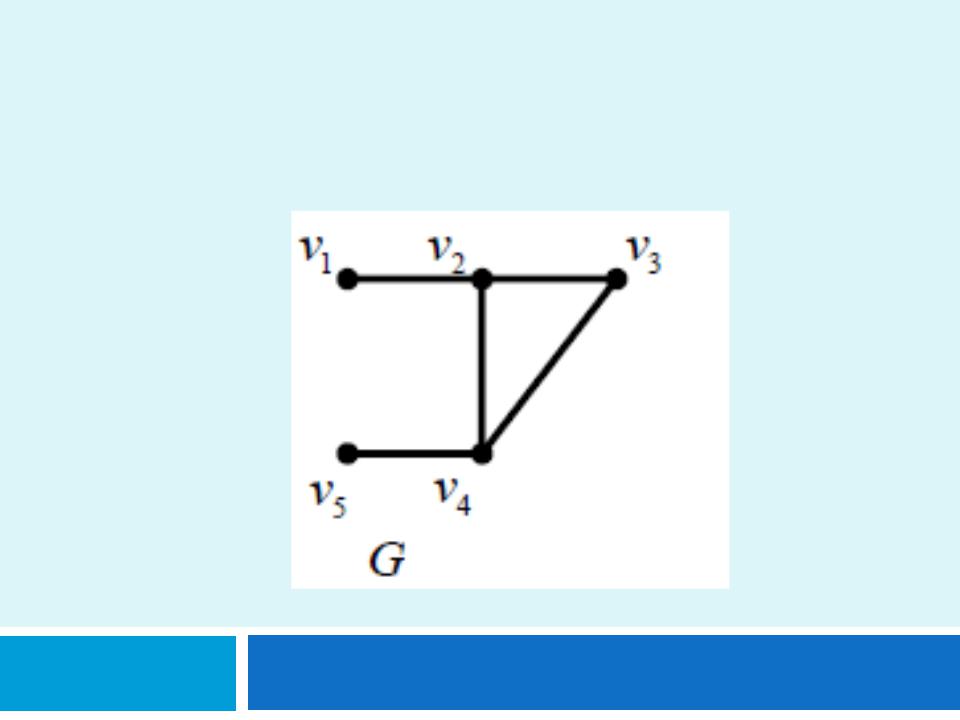
Задача 2.
Пусть дан граф G=(V,E). Выполнить над графом операцию удаления вершины v3.
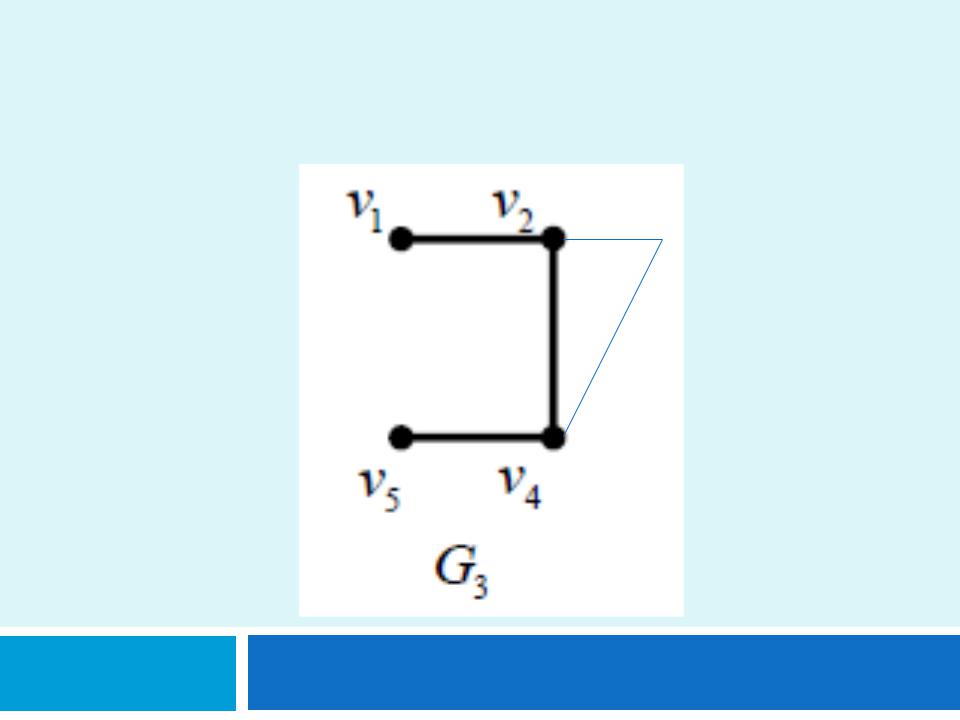
Задача 2.
Пусть дан граф G=(V,E). Выполнить над графом операцию удаления вершины v3.
Решение.
v3

Задача 2.
Пусть дан граф G=(V,E). Выполнить над графом операцию удаления вершины v3.
Решение.
