
4802
.pdf
Т. Н. СТОРОДУБЦЕВА
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Воронеж 2018
2
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный лесотехнический университет имени Г. Ф. Морозова»
Т. Н. СТОРОДУБЦЕВА
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
методические указания к выполнению расчетно-графической работы
«Геометрические характеристики плоских сечений» для студентов по направлению подготовки 15.03.02 Технологические машины и оборудование
Воронеж 2018
3
УДК 539.3 Стородубцева Т. Н. Сопротивление материалов [Электронный ресурс] :
методические указания к выполнению расчетно-графической работы «Геометрические характеристики плоских сечений» для студентов по направлению подготовки 15.03.02 Технологические машины и оборудование / Т. Н. Стородубцева; М-во образования и науки РФ, ФГБОУ ВО «ВГЛТУ». – Воронеж,
2018. – 48 с.
Печатается по решению учебно-методического совета
ФГБОУ ВО «ВГЛТУ» (протокол № __ от ____________ 20__ г.)
Рецензент заведующий кафедрой электротехники и автоматики ФГБОУ ВО ВГАУ им. Императора Петра 1, д-р техн. наук, проф. Д. Н. Афоничев
Методические указания к расчетно-графической работе по сопротивлению материалов «Геометрические характеристики плоских сечений» рекомендуются студентам, аспирантам и магистрантам технических вузов при решении, подготовке и защите индивидуальных расчетно-графических работ, при подготовке к практическим занятиям, а также при подготовке к сдаче зачетов и экзаменов.
4
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ…………………………………………………………….............. 4
1.ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ …………………………………………………………………... 5
1.1.Определение осевых моментов инерции ……………………………. 7
1.2.Определение полярного момента инерции круга……………………. 9
1.3.Определение осевых моментов инерции круга………………………. 9
1.4.Осевые моменты сопротивления……………………………………… 10
1.5.Определение осевых моментов инерции и моментов сопротивления………………………………………………………….. 10
1.6. Определение осевых моментов сопротивления……………………… |
12 |
1.7. Определение полярных моментов инерции и моментов |
|
сопротивления…………………………………………………………. |
12 |
1.8. Изменение моментов инерции………………………………………… |
14 |
1.9.Изменение статических моментов……………………………………. 17
2.ГРАФИЧЕСКИЙ СПОСОБ – ПОСТРОЕНИЕ КРУГА МОРА…………. 20 2.1. Определение моментов инерции с помощью круга Мора
(графическим способом)……………………………………………….. 20
2.2.Построение эллипса инерции………………………………………….. 21
3.ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ…………………………………………………………………… 23
3.1. Порядок выполнения расчетно-графической работы № 1…………… 23
3.2.Пример выполнения расчетно-графической работы № 1 - сечение состоящее из швеллера и неравнополочного уголка………... 24
4.ПРОВЕРКА РАСЧЕТА РГР № 1 НА ЭВМ……………………................... 33
4.1.Ввод данных в интерфейсное окно……………………………………. 33
4.2. Пример распечатки полученных данных……………………………… |
34 |
|
Библиографический список…………………………………………………… |
36 |
|
ПРИЛОЖЕНИЯ………………………………………………………………... |
37 |
|
Приложение 1. |
Прокатные профили двутавры……………………………… |
38 |
Приложение 2. |
Прокатные профили швеллеры……………………………… |
40 |
Приложение 3. Прокатные профили неравнобокие уголки………………… |
42 |
|
5
Приложение 4. Прокатные профили равнобокие уголки………………….... 44
ВВЕДЕНИЕ
Как только человек начал заниматься строительством, он убедился в необходимости располагать сведениями о сопротивлении материалов, на основе которых можно было бы выбрать надежные размеры частей сооружения. Уже в Древнем Египте и Греции люди могли определять центр тяжести, пользовались рычагом. В период средневековья многие знания были утрачены, и лишь в эпоху Возрождения задачи механики и статики стали успешно решаться. Первые попытки установления безопасных размеров элементов сооружений аналитическим путем относятся к XVII в, который был эпохой быстрого развития математики, астрономии, естественных наук. Первая книжка по сопротивлению материалов была опубликована французским ученым А. Навье (1785 - 1836) [1-3].
Сопротивление материалов – наука о прочности, жесткости и устойчивости отдельных элементов конструкций (сооружений и машин) [2].
Инженеру любого направления часто приходится производить расчеты на прочность. Неправильный расчет самой незначительной, на первый взгляд, детали может повлечь за собой очень тяжелые последствия – привести к разрушению конструкции в целом. При проведении расчета на прочность необходимо стремиться к сочетанию надежности работы конструкции с ее дешевизной, добиваться наибольшей прочности при наименьшем расходе материала.
Сопротивление материалов – одна из сложных дисциплин, изучаемых в высших технических учебных заведениях; занятия по этому курсу обязательно должны сопровождаться составлением конспекта и решением задач. Если при решении задач возникнут затруднения, следует воспользоваться имеющимися в задачниках указаниями и решениями, но совершенно необходимо научиться решать задачи самостоятельно. Следует также научиться делать выводы формул. При этом необходимо обращать особое внимание на физическую сущность явления и на те допущения и ограничения, которые делаются в процессе выводов .
На деформацию и напряжение твердого тела существенно влияет форма его поперечного сечения. Поэтому в данном методическом указании рассматривают основные геометрические характеристики поперечных сечений объекта, определяющие сопротивление различным видам деформации без учета его фи-
6
зических свойств. К ним относятся площади поперечного сечений, статические моменты, моменты инерции и моменты сопротивления [1-5].
1. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
Втеории изгиба важную роль играют моменты инерции, поэтому следует рассмотреть этот вопрос предварительно в виде самостоятельной темы.
Втеории изгиба важную роль играют моменты инерции, поэтому следует рассмотреть этот вопрос предварительно в виде самостоятельной темы. Перед изучением этой темы полезно по учебнику теоретической механики повторить материал о статическом моменте и о нахождении центров тяжести плоских фигур. При вычислении моментов инерции надо помнить, что они представляют
собой интегралы или типа x2 dA (осевой, или экваториальный, момент инер-
A
ции относительно оси у) или типа xydA (центробежный момент инерции от-
A
носительно осей x и у).
Необходимо запомнить, что теорема о переносе осей I y1 I y a2 I
справедлива только в том случае, если ось у проходит через центр тяжести фигуры. Формула переноса осей наглядно показывает, что наименьшим из моментов инерции относительно нескольких параллельных осей является момент инерции относительно той оси, которая проходит через центр тяжести.
Наименьшим из моментов инерции относительно центральных осей, наклоненных под разными углами, является момент инерции относительно одной из главных центральных осей. Относительно другой главной оси, перпендикулярной к первой, момент инерции имеет, наоборот, наибольшее значение. Центробежный момент инерции относительно главных осей равен нулю; при этом совсем не обязательно, чтобы главные оси проходили через центр тяжести, так как через любую точку, лежащую в плоскости фигуры, можно провести такие две взаимно перпендикулярные оси, относительно которых центробежный момент инерции будет равен нулю. В теории изгиба весьма важную роль играют главные центральные оси, положение которых для несимметричных сечений
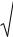
7
определяют так:
1)сначала проводят случайные оси, вычисляют статические моменты сечения относительно этих осей (разделив предварительно сложную фигуру на ряд простых фигур) и находят положение центра тяжести сечения;
2)проводят через центр тяжести всего сечения оси, параллельные первоначально выбранным случайным осям, и находят при помощи теоремы о переносе осей центробежный и осевые моменты инерции сечения относительно этих новых осей;
3)находят положение главных центральных осей x и y по формуле
|
tg2 0 |
|
2I xc yc |
|
; |
|
|||
|
|
|
I |
|
|
|
|||
|
|
|
I |
xc |
|
|
|
||
|
|
|
|
|
yc |
|
|||
4) находят главные центральные моменты инерции. |
|
||||||||
Для проверки правильности вычислений |
I x и I y |
можно использовать |
|||||||
равенства: I x I y I xc |
I yc |
и I x y . |
|
|
|
|
|
|
|
Следует иметь в виду, что при помощи этих равенств можно проверить вычисления только по п.п. 3 и 4; соблюдение этих равенств не гарантирует правильности вычислений, сделанных в п.п. 1 и 2.
Если сечение состоит из ряда прокатных профилей, то необходимо при вычислениях пользоваться данными таблиц сортамента. При определении центробежного момента инерции уголка (равнобокого или неравнобокого) не следует делить площадь этого уголка на два прямоугольника; сначала можно найти центробежный момент инерции всего уголка относительно осей, проходящих через центр тяжести параллельно полкам, при помощи формулы, в которой использованы обозначения таблиц сортамента:
|
|
|
I x0 |
I y0 |
sin 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
; или |
I |
|
|
|
I |
|
I |
|
(I |
|
I |
|
I |
|
) I |
; |
||||||
xy |
|
2 |
0 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
xy |
|
|
|
x |
|
y |
|
x |
|
y |
|
U min |
|
U min |
|||||
|
|
|
|
|
|
|
I |
|
|
|
|
I x Imin |
; |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
xy |
|
tg |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где I x0 и I y0 – главные центральные моменты инерции, значения кото-
8
рых даны в таблицах сортамента; после этого надо применить формулу переноса осей и найти центробежный момент инерции уголка относительно центральных осей всего сечения.
При пользовании формулой поворота осей надо обязательно обратить внимание на знак угла, а если для совмещения оси х0 с осью х надо повернуть ось х0 по часовой стрелке, то угол следует считать отрицательным.
Вопросы для самопроверки. 1. По каким формулам находят координаты центра тяжести плоской фигуры? 2. Чему равна сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей? 3. Какие оси называются главными? 4. Для каких фигур можно без вычислений установить положение главных центральных осей? 5. Относительно каких центральных осей осевые моменты инерции имеют наибольшее и наименьшее значения?
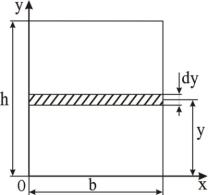
1.1. Определение осевых моментов инерции I x
Определение осевых моментов инерции I x для фигуры, показанной
на рис. 1.1.
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
h |
|
I x y2dA y2bdy b y2dy |
|||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
||||
|
|
|
by3 |
|
|
h |
|
|
bh3 |
|
; |
|
|||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
3 |
|
|
0 |
|
|
|
3 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
I |
|
|
bh3 |
|
, |
I |
|
|
hb3 |
. |
|||||||
x |
|
y |
|
||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
3 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Рис. 1.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Центробежный момент инерции площади сечения I xy |
|
относительно |
|||||||||||||||
осей x и y есть интеграл вида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I xy xydA, |
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.1) |
|||
A
9
где: x, y - координаты центра тяжести элементарной площадки dA; dА -
элементарная площадка A b h . |
|
|
|
|
|
||
По свойству разбиения определенного интеграла, |
I xy |
может быть пред- |
|||||
|
|
|
|
|
|
|
|
|
I xy xyA1 xyA2 |
xyAn |
|
n |
i |
|
|
|
|
|
|
||||
ставлен так: |
|
I xy . |
|||||
|
A1 |
A2 |
An |
|
i 1 |
|
|
|
|
|
|
|
|||
Следовательно, центробежный момент площади сечения относительно осей x и y равен сумме центробежных моментов частей площади сечения относительно тех же осей.
Так как в выражении (1.1) x и у координаты центра тяжести элементарной площадки dA, то подинтегральное выражение может быть любого знака, а интеграл может быть положительной величиной или отрицательной, или равной нулю. Оси, относительно которых центробежный момент равен нулю, называют главными. Ось симметрии фигуры всегда является главной осью.
Размерность центробежного момента площади сечения - длина в четвертой степени (м4, см4, мм4).
Центробежный момент инерции площади сечения относительно осей используется для нахождения положения главных осей и вычисления осевых моментов инерции относительно главных осей.
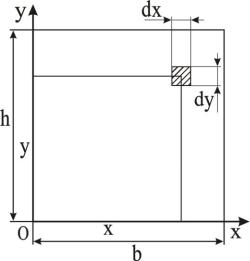
1.1.1. Пример. Для фигуры, показанной на рис. 1.2, определить I xy . dA dx dy;
b h
I xy x ydA x y dxdy
|
|
|
|
A |
|
|
|
0 0 |
|
|
|
|
|
|
|
|
|
|
|
b |
h |
|
|
|
b |
|
|
|
|
|
h |
|
|
||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
y 2 |
|
|
|
|
|||||
x |
|
y dy |
|
dx x |
|
|
|
|
dx |
|
|||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||
0 |
|
|
0 |
|
|
0 |
|
|
|
|
|
0 |
|
|
|||||
|
|
|
|
|
|||||||||||||||
|
h2 |
|
b |
|
h2 |
|
x2 |
|
|
b |
2 b2 |
|
|
||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
xdx |
|
|
|
|
h |
; |
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||
2 |
|
|
0 |
|
|
2 |
2 |
|
|
0 |
|
|
|
4 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
10
Рис. 1.2.
I xy h2 b2 .
4
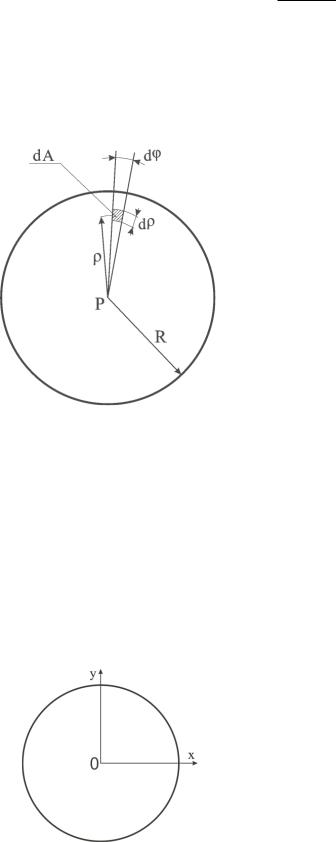
1.2. Определение полярного момента инерции круга, показанной
на рис. 1.3.
dA d d ;
|
|
|
|
|
|
|
|
|
|
|
2 R |
|
|
|
|
|
|
|
||
|
|
I p |
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||
|
|
|
|
dA |
|
|
|
d |
d |
|||||||||||
|
|
|
|
A |
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
R4 |
|
R |
4 |
|
|
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
; |
|
||||||
|
|
|
|
|
4 |
|
|
|
4 |
|
|
|||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
πR4 |
. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рис. 1.3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как R |
D |
, то I |
|
|
πD4 |
. |
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
ρ |
32 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Полярный момент инерции используется при расчетах углов закручива- |
||||||||||||||||||||
ния стержней (и валов) круглого поперечного сечения и при определении напряжения в произвольных точках поперечного сечения таких сечений (валов).
1.3. Определение осевых моментов инерции круга, показанной на рис. 1.4.
Оси x и y являются осями симметрии круга и I x I y .
Так как I p I x I y , то I p 2I x 2I y . Следовательно
