Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежская государственная лесотехническая академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

4619

.pdf

Скачиваний:

Добавлен:

08.01.2021

Размер:

1.23 Mб

Скачать

☆

1 / 31 2 3 > Следующая >>>

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ЛЕСОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ Г. Ф. МОРОЗОВА»

МАТЕМАТИКА

Методические указания для самостоятельной работы студентов

по направлению подготовки 35.03.01 Лесное дело

Воронеж 2020

УДК 517.9

Зенина, В.В. Математика [Электронный ресурс]: методические указания для самостоятельной работы студентов по направлению подготовки 35.03.01 Лесное дело / В.В. Зенина, И.В. Сапронов, С.С. Веневитина; М-во науки и высшего образования РФ, ФГБОУ ВО «ВГЛТУ». – Воронеж, 2020. – 27 с.

Одобрено решением учебно-методического совета ФГБОУ ВО «ВГЛТУ»

Рецензент д-р физ.-мат. наук, профессор Воронежского государственного университета С.П. Зубова

Методические указания для самостоятельной работы по дисциплине «Высшая математика» предназначены для студентов ФГБОУ ВО «Воронежский государственный лесотехнический университет», обучающихся по направлению подготовки 35.03.01 – Лесное дело.

Дисциплина «Высшая математика» изучается в течение одного семестра, в котором необходимо выполнять самостоятельную работу.

Предложены несколько вариантов самостоятельных работ по каждому из разделов математики.

Материалы данной учебно-методической разработки по содержанию и объёму соответствуют задачам дисциплины и требованиям стандарта соответствующего направления подготовки.

Оглавление

1. Неопределенный интеграл……………………………………………….... 4

1.1. Теоретическая часть……………………………………………………….. 4

1.1.1.Понятие неопределенного интеграла………………………………….... 4

1.1.2.Свойства неопределенного интеграла………………………………….. 5

1.1.3.Таблица основных неопределенных интегралов………………………. 5

1.1.4.Основные методы интегрирования……………………………………... 7

1.2. Практическая часть…………………………………………………………. 8

1.3.Индивидуальные задания………………………………………………….. 11

1.4.Вопросы для самоконтроля и повторения………………………………… 13

2. Определенный интеграл………………………………………………….... 14

2.1.Теоретическая часть…………………………………………………………. 14

2.1.1.Условия существования определенного интеграла…………………….. 14

2.1.2.Основные свойства определенного интеграла…………………………... 15

2.1.3.Основная формула интегрального исчисления………………………….. 17

2.1.4.Основные правила интегрирования……………………………………... 17

2.1.5.Геометрические приложения определенного интеграла……………….. 18

2.2.Практическая часть……………………………………………………….. 20

2.3.Индивидуальные задания…………………………………………………. 24

2.4.Вопросы для самоконтроля и проверки…………………………………… 26 Библиографический список……………………………………………………... 27

f ( x ).

f ( x )

1. Неопределенный интеграл

1.1. Теоретическая часть

1.1.1. Понятие неопределенного интеграла

Одна из основных задач дифференциального исчисления – нахождение производной заданной функции. Множество вопросов математического анализа и приложений в разнообразных науках приводит к другой задаче: по данной функции найти такую функцию F( x ), производная которой равна функции

Функция F( x ) называется первообразной функции

f ( x ) на интервале

a;b

, если для любого x

a;b

выполняется равенство

F ( x )

f ( x ).

Например, первообразной функции

f ( x )

x2 , x

Ў , является функция

F( x )

, так как

F ( x )

f ( x ).

Очевидно,

что

первообразными

будут

также

любые

функции

F( x )

C , где C – постоянная, поскольку

F ( x )

f ( x ),

x Ў .

Теорема 1.1.

Если функция F( x )

является первообразной функции

f ( x ) на

a;b , то множество всех

первообразных

для

f ( x )

задается

формулой F( x )

C , где C – постоянное число.

Множество

всех

первообразных

функций

F( x )

для f ( x )

называется неопределенным интегралом от функции

f ( x ) и обозначается

символом

f ( x )dx .

Таким образом, по определению

f ( x )dx

F( x )

C .

Здесь

f ( x ) называется подынтегральной

функцией,

f ( x )dx –

подынтегральным выражением,

x – переменной интегрирования,

– знаком

S , означающая

неопределенного интеграла (это стилизованная латинская буква суммирование).

Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции. Интегрирование является операцией, обратной дифференцированию. Для проверки правильности выполнения интегрирования нужно продифференцировать результат и получить при этом подынтегральную функцию.

Геометрически неопределенный интеграл представляет собой семейство «параллельных» кривых y F( x ) C, где каждому числовому значению C соответствует определенная кривая семейства. График каждой первообразной

(кривой) называется интегральной кривой.

1.1.2. Свойства неопределенного интеграла

Прежде всего, укажем свойства, которые непосредственно вытекают из определения неопределенного интеграла.


1.	d	f ( x )dx		f ( x )dx ,		f ( x )dx		f ( x ) .
2.		dF( x )	F( x ) C .
Следующие два свойства называются линейными свойствами
неопределенного интеграла.
3.		kf ( x )dx	k	f ( x )dx .
4.		f ( x )	g( x ) dx		f ( x )dx		g( x )dx .
Отметим свойство инвариантности формулы интегрирования.
5.		Если	f ( x )dx		F( x )	C ,	то и	f ( u )dx F( u ) C , где

u ( x ) – произвольная функция, имеющая непрерывную производную.

1.1.3. Таблица основных неопределенных интегралов

Интегралы в приводимой ниже таблице называются табличными. Их следует знать наизусть. В интегральном исчислении нет простых и универсальных правил отыскания первообразных от элементарных функций, как в дифференциальном исчислении. Методы нахождения первообразных (т.е.

интегрирования функции) сводятся к указанию приемов, приводящих данный (искомый) интеграл к табличному. Следовательно, необходимо знать табличные интегралы и уметь их узнавать. Часть формул таблицы непосредственно следует из определения интегрирования как операции, обратной дифференцированию. Справедливость всех формул легко проверить дифференцированием.

1. x dx	x	1	C ,	1.


		1

C ,

0 .

a x

a xdx

1 .

ln a

exdx ex

C .

sin xdx

cos x

C .

cos xdx

sin x

C .

tgx C .

cos2 x

ctgx

C .

sin2 x

arctgx

C .

1 x2

10.

arctg

C .

11.

arcsin x

C .

12.

arcsin

C .

13.

C .

14.

C .

1.1.4. Основные методы интегрирования

Метод непосредственного интегрирования

Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.

Метод подстановки

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования. При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.

	Пусть требуется вычислить интеграл f ( x )dx . Сделаем подстановку
x	( t ) , где	( t ) – функция, имеющая непрерывную производную. Тогда
dx	( t )dt	и на основании свойства инвариантности формулы

интегрирования получаем формулу интегрирования подстановкой или формулой замены переменных

f ( x )dx f ( ( t )) ( t )dt . (1.1)

После нахождения интеграла правой части этого равенства следует

перейти от новой переменной интегрирования t назад к переменной x .
Иногда целесообразно подбирать подстановку в виде t		( x ) , тогда
f ( ( x )) ( x )dx	f ( t )dt . Другими словами, формулу	(1.1)	можно

применять справа налево.

С помощью метода замены переменной можно вывести следующие

основные правила интегрирования:

Если

f (x)dx

F(x)

C , то

f (kx b)dx

F (kx b) C ;

f (x)dx

f (x)

C ;

f (x)

f (x)dx

f (x)

C .

f (x)


Метод интегрирования по частям
Пусть u	u( x )	и v	v( x )		–	функции, имеющие непрерывные
производные.	Тогда	d( uv )	u dv		v du . Интегрируя		это	равенство,
получим		d( uv )		udv		vdu или
		udv		uv		vdu .		(10.2)
Полученная формула называется формулой интегрирования по частям.
Она дает возможность		свести	вычисление интеграла udv				к	вычислению

интеграла vdu , который может оказаться существенно более простым, чем

исходный.

Укажем некоторые типы интегралов, которые удобно вычислять методом

интегрирования по частям.

Интегралы вида

P( x )ekxdx ,

P( x ) sin kxdx ,

P( x )cos kxdx ,

где

P( x ) –

многочлен, k –

число. Удобно положить u P( x ), а за dv

обозначить все остальные сомножители.

Интегралы

вида

P( x )arc sin xdx ,

P( x )arccos xdx ,

P( x )ln xdx ,

P( x )arctgxdx ,

P( x )arcctgxdx .

Удобно положить

P( x )dx , а за u обозначить остальные сомножители.

Интегралы вида

eax sinbxdx ,

eax

cosbxdx ,

где a и b – числа.

За u можно принять функцию u

eax .

1.2. Практическая часть

Пример 1. Вычислить интеграл

x x

dx .

Преобразуем подынтегральную функцию:

x x

Тогда

x x 2

dx = x4

x 2

dx =

x4dx

x 2 dx 2

x 2

2ln

C .

При вычислении использовали 3-е и 4-е свойства неопределённого

интеграла и табличные интегралы №1 и №2.

Пример 2.

Вычислить интеграл

x 3 5

x2 dx .

Делаем

замену

t ,

тогда

2xdx

dt и

xdx

dt .

Следовательно,

= 1

1 3 t

= 3 3 5 x2

x 3 5 x2 dx =

t 3dt

3 C

C .

xdx

2 dt

Пример 3.

Вычислить интеграл

arctg 2 x

dx .

Делаем замену

arctgx

t ,

тогда

dt .

Следовательно,

arctg 2 x

dx =

t2dt

arctg3 x

C .

Пример 4.

Вычислить интеграл

xsin

5x dx .

Воспользуемся формулой интегрирования по частям:

udv

vdu .

sin(5x)dx

x sin(5x)dx

x cos(5x)

du dx

cos(5x)

cos(5x)dx

x cos(5x)

sin(5x)

C .

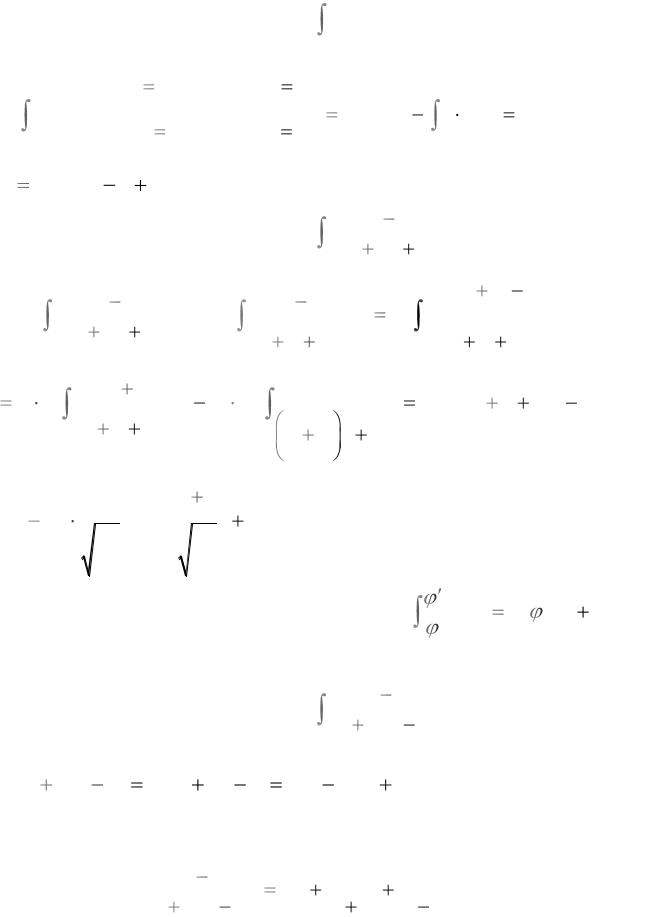
Пример 5.

Вычислить интеграл

ln 2x dx .

ln(2x)

ln 2x dx =

xln(2x)

C .

Пример 6.

Вычислить интеграл

dx .

3x2

2x 1

5x 3

dx =

3x 10

2x 1

1 11

arctg

C .

(x)

При решении мы воспользовались

правилом

(x)

и табличным интегралом № 10.

(x)

Пример 7.

Вычислить интеграл

dx .

2x2

а)

Знаменатель подынтегральной функции разложим на множители:

2x2

3x x x2

2x 3 x x 1 x 3 .

б)

подынтегральную функцию представим в виде суммы простейших

дробей:

2x2

x 3

x 1

Тогда

1 / 31 2 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.01.20211.22 Mб24613.pdf
#
08.01.20211.22 Mб24614.pdf
#
08.01.20211.22 Mб34615.pdf
#
08.01.20211.23 Mб54616.pdf
#
08.01.20211.23 Mб44618.pdf
#
08.01.20211.23 Mб04619.pdf
#
08.01.2021200.59 Кб1462.pdf
#
08.01.20211.24 Mб24620.pdf
#
08.01.20211.24 Mб54621.pdf
#
08.01.20211.24 Mб34622.pdf
#
08.01.20211.24 Mб24623.pdf