Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежская государственная лесотехническая академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

4619

.pdf

Скачиваний:

Добавлен:

08.01.2021

Размер:

1.23 Mб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

			7x 15				A x 3 x 1 Bx x 1 Cx x 3
										,
		x3	2x2							,
		x3	2x2		3x				x x 3 x 1
Следовательно,
			7x 15 A x 3 x 1 Bx x 1 Cx x 3 .
Определим постоянные							A, В и С .
Если	x		0 ,	то	15		3A и	A	5;
если	x		3,	то		36 12B		и	B 3;
если	x		1,	то	8		4C и	C	2 .

Тогда

dx =

dx = 5

2x2

x 3 x 1

x 3

5ln

3ln

2ln

x 1

C .

1.3.

Индивидуальные задания

Задача.

Найти неопределенные интегралы.

Вариант 1.

x dx ;

dx ;

;

e12 x

7dx ;

e x2

xdx ;

ln6 x

dx ;

arctgxdx ;

ex sin xdx ;

dx ;

10)

dx .

3x2 4x

(x2

1)(x

dx ;

(x2

x )2

dx ;

Вариант 2.

dx ;

cos( 2

9x )dx ;

;

2 x

dx ;

x e xdx ;

cos2

x 1

tgx

x2 cos(2x)dx ;

dx ;

10)

dx .

2x2

1)(x2

cos(2x)

Вариант 3.

3 x2

dx ;

;

cos2 x sin2

cos2( 5x

1 8 x

sin x

lg x

dx ;

x e

;

cos3 x

dx ;

10)

3x2

sin x

cos x

Вариант 4.

dx ;

5 x4

dx ; 3)

cos 4xdx ;

;

ctg7 x

dx ;

6) ecos x

sin xdx ;

cos(2x)dx ;

sin2( 4x

sin2

8)e x sin xdx ;

Вариант 5. 1)

4)sin 2x dx ;

8)x2 e 2 xdx ;

Вариант 6. 1)

4)cos 5x dx ;

8)sin 3x cos

Вариант 7. 1)

9)	3x	1	dx ;	10)	2x	1	dx .

	4x2	x 2			x 1 2	x 2

																										1 3
7x4				3x							2		dx ; 2)											x		1 3			dx ; 3)			e2 x 5dx ;

																								x
							5					x3
							5					x3

5)			cos x					dx ;					6)			tg						x	dx ;			7)				x2 sin(2x)dx ;
5)								dx ;					6)										dx ;			7)				x2 sin(2x)dx ;
		3 sin2 x																	x
9)		2x			3						dx ;		10)							x				1				dx .

	3x2				x			1									x	2 2								x
		2																							3
7x3																(		x						2)	3						e2 x 10dx ;
						6						dx ;	2)			(		x						2)		dx ;				3)
				x		6						dx ;	2)								x					dx ;				3)
				x																	x
5)				e2 x					dx ;				6)				xdx							;		7)				xln	x	2	1 dx ;
5)		4			e2 x				dx ;				6)				x4	1						;		7)				xln	x		1 dx ;
		4			e2 x												x4	1
5x dx ;		9)										2x	1	dx ;				10)												dx	.

										4x2			x 3														x x2			x 2
8x	3x				4						dx ;		2)		ctg 2 xdx ;											3)				sin( 3			6x )dx ;



		4				x

		dx							1							x2 dx					e x cos 2x dx ;
4)				;	5)	cos x						dx ;		6)				;	7)
		x2	9												1		x3
										x

8)	arctgxdx ;				9)			x	6				dx ;		10)		2		sin x	dx .
							2x2
									7x		1						2		cos x

								1
Вариант 8.			1)			4		1					6							5			x4		dx ;			2)				tg 2 xdx ;											3)	e2 5xdx ;
																				5
									x3
									x3
4)	3x 4 4 dx ;					5)								cos xdx									;			6)				xdx				;						7)			x2 sin		3x dx ;
4)	3x 4 4 dx ;					5)																	;			6)								;						7)			x2 sin		3x dx ;
														5 sin2 x																x4	1
8)	arccos xdx ;			9)							2 x											dx ;				10)							x				1					dx .

								2x2									x			1										x2	3							x		5
																		5															dx													x
					3x2
Вариант 9.			1)							2x													dx ;			2)															;			3)	e 3 dx ;
Вариант 9.			1)							2x													dx ;			2)			cos 2x sin2												;			3)	e 3 dx ;
																			x										cos 2x sin2											x

																																		ln x					dx ;
4)	cos(1	2x )dx ;				5)									x3			5			x4			1dx ;				6)						ln x									7)	x2 ln xdx ;
4)	cos(1	2x )dx ;				5)									x3						x4			1dx ;				6)															7)	x2 ln xdx ;
																																			x
8)	e x cos 2xdx ;					9)										2x				1				dx ;				10)											dx					.
8)	e x cos 2xdx ;					9)					3x2									x			3	dx ;				10)					4sin x							5cos x				.
											3x2									x			3										4sin x							5cos x
					5x4			2												1				dx ;						1	x 2												sin( 6x		8 )dx ;
Вариант 10.		1)																								2)										dx 3)
										3x

																		3			x2
																		3			x2									x		x

	23 5x dx ;						cos					x
4)				5)			cos					x				dx ;								6)			x3	3		x4 dx ;										7)				x cos(2x)dx ;

										x
										x
8)	x2exdx ;		9)			3x		1							dx ;									10)						dx								.
8)	x2exdx ;		9)		x2										dx ;									10)														.
					x2		3x					1															3sin x			4cos x

1.4. Вопросы для самоконтроля и повторения.

1.Какая функция называется первообразной?

2.Сформулируйте определение неопределенного интеграла.

3.Перечислите основные свойства неопределенного интеграла.

4.Запишите табличные интегралы (их надо выучить наизусть).

5.В чем заключается метод замены переменной? Приведите примеры.

6.Напишите формулу интегрирования по частям.

7.Укажите некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям.

2. Определенный интеграл

2.1. Теоретическая часть

2.1.1. Условия существования определенного интеграла

Пусть функция

f ( x ) задана на отрезке

a; b . Разобьем отрезок

a; b

на n произвольных частей точками:

a x0

K xi

xi 1

K xn

В каждом частичном отрезке xi

,xi

выберем произвольную точку ci :

xi 1

xi ,

1,2,K ,n ,

и вычислим значение функции в ней, т.е. величину

f ( ci ) .

Умножим найденное значение функции

f ( ci ) на длину

xi 1

соответствующего частичного отрезка: f ( ci )

xi .

Составим сумму всех таких произведений:

f ( c1 ) x1

f ( c2 )

f ( cn )

f ( ci )

xi .

(2.1)

i 1

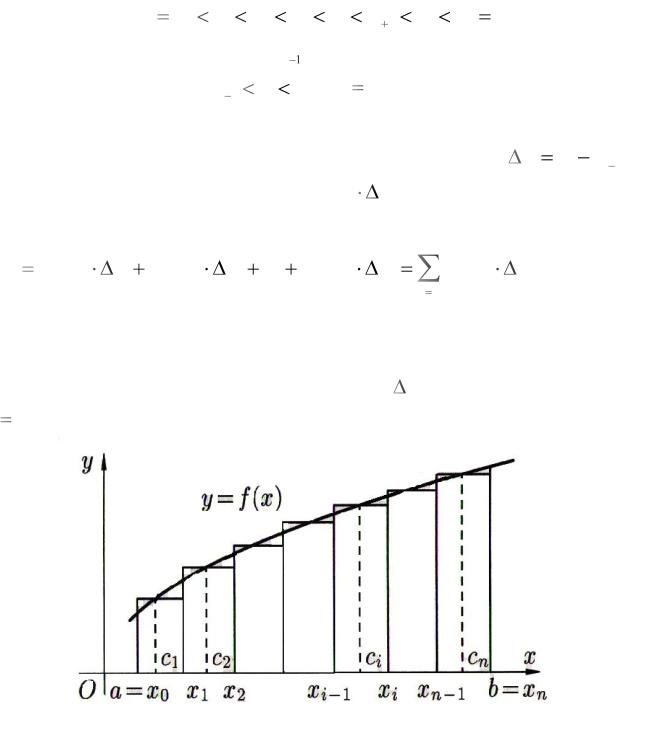
Сумма вида (2.1) называется интегральной суммой функции

f ( x ) на

отрезке

a; b . Геометрический смысл величины Sn

указан на рис 1: это сумма

площадей прямоугольников с

основаниями

и высотами

f ( ci )

(i 1,2,K ,n ).

Рис. 1

Обозначим через длину наибольшего частичного отрезка:

			max		xi .
			1 i	n
Конечный предел		I интегральной		суммы		Sn	при	0 , если		он
существует,	называется	определенным	интегралом				от функции		f ( x )	на
		b
отрезке a; b	и обозначается f ( x )dx . Таким образом,
		a
	b		n
		f ( x )dx lim		f	ci	xi .			(2.2)
	a	n	i	1
	a	0	i	1
Числа a и b называются соответственно						нижним		и	верхним
пределами интегрирования, f ( x ) – подынтегральной функцией,									f ( x )dx –

подынтегральным выражением, x – переменной интегрирования, отрезок a; b – областью (отрезком) интегрирования.

Функция y f ( x ), для которой на отрезке a; b существует

определенный интеграл f ( x )dx называется интегрируемой на этом отрезке.

Ответ на вопрос о том, какие функции являются интегрируемыми, дают следующие теоремы, которые мы приводим без доказательства.

Теорема 2.1 (Коши). Если функция f ( x ) непрерывна на отрезке a; b ,

то она интегрируема на нем.

Теорема 2.2. Если определенная и ограниченная на отрезке a; b

функция f ( x ) имеет конечное число точек разрыва, то она интегрируема на

этом отрезке.
Теорема 2.3.	монотонная на отрезке a; b функция f ( x )

интегрируема на этом отрезке.

2.3.2. Основные свойства определенного интеграла

1. Определенный интеграл с одинаковыми пределами интегрирования равен нулю:

f ( x )dx 0 .

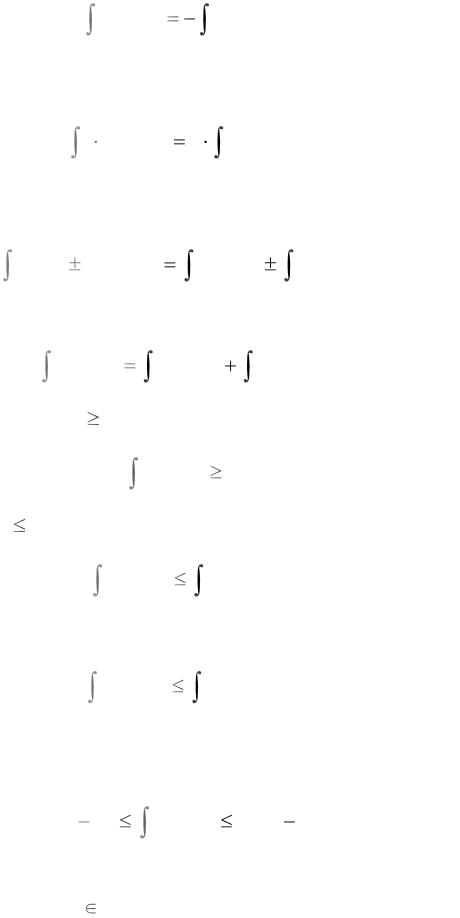
2.По определению полагается:

f ( x )dx

f ( x )dx .

Постоянный множитель можно выносить за знак определенного

интеграла:

c f ( x )dx

f ( x )dx .

Определенный интеграл от алгебраической суммы функций равен

алгебраической сумме их определенных интегралов:

f ( x )

g( x ) dx

f ( x )dx

g( x )dx .

Для любых чисел a,b и c

имеет место равенство

f ( x )dx

f ( x )dx .

Если функция

f ( x )

0 всюду на отрезке a; b , то

f ( x )dx

0 .

Если

f ( x )

g( x ) всюду на отрезке

a; b , то

f ( x )dx

g( x )dx .

Если функция

f ( x ) интегрируема на

a; b , то

f ( x )dx

f ( x )

dx .

Если

M и

m – соответственно максимум и минимум функции

f ( x ) на отрезке a; b , то

m( b

a )

f ( x )dx

M ( b

a ).

10.«Теорема о среднем». Если функция f ( x ) непрерывна на отрезке

a; b , то существует точка c a;b такая, что

Число	f ( c )	1

		b a
		b a

f ( x ) на отрезке a; b .

f ( x )dx f ( c ) ( b a ).

f ( x )dx называется средним значением функции

2.1.3. Основная формула интегрального исчисления

Простым и удобным методом вычисления определенного интеграла от непрерывной функции является формула Ньютона-Лейбница:

f ( x )dx F( x )	ba F( b ) F( a ) .	(2.3)

2.1.4. Основные правила интегрирования

Замена переменной в определенном интеграле

Теорема 2.4. Пусть:
1)	f ( x ) – непрерывная функция на отрезке a; b ;
2)	функция	( t ) –		дифференцируема на				;	,
	( t ) – непрерывна на				;
и множеством значений функции							( t ) является отрезок a; b ;
3)	( )	a,	(	)	b .
Тогда справедлива формула
			b
			f ( x )dx			f	( t )	( t )dt .	(2.4)
			a
Формула (2.4) называется формулой замены переменной в определенном
интеграле.
Отметим, что:
1)	при вычислении определенного интеграла с помощью замены
переменной возвращаться к старой переменной не требуется;
2)	часто вместо замены переменной x							( t )	применяют подстановку

t g( x ) ;

3) не следует забывать менять пределы интегрирования при замене

переменных!
Интегрирование по частям в определенном интеграле
Теорема 2.5. Пусть функции			u( x ) и ( x ) имеют	непрерывные
производные на отрезке a; b ; тогда справедлива формула
b			b
ud	u	ba	du .	(2.5)
ud			du .	(2.5)
a			a
a			a

Равенство (2.5) называется формулой интегрирования по частям в определенном интеграле.

2.1.5. Геометрические приложения определенного интеграла

Площадь плоской фигуры

Рассмотрим на плоскости Oxy фигуру, ограниченную графиком

непрерывной	и положительной функции	f ( x ), осью Ox и вертикальными
прямыми x	a и x b (рис 2). Такая	фигура называется криволинейной
трапецией.

Рис. 2

Площадь криволинейной трапеции равна определенному интегралу от функции f ( x ) на отрезке a; b :

		b
		S	f x	dx .
		a
Отметим, что если криволинейная трапеция расположена «ниже» оси Ox
( f ( x ) 0), то ее площадь может находиться по формулам
	b				b
	b				b
S	f	x dx	или	S	f	x	dx	.
	a				a
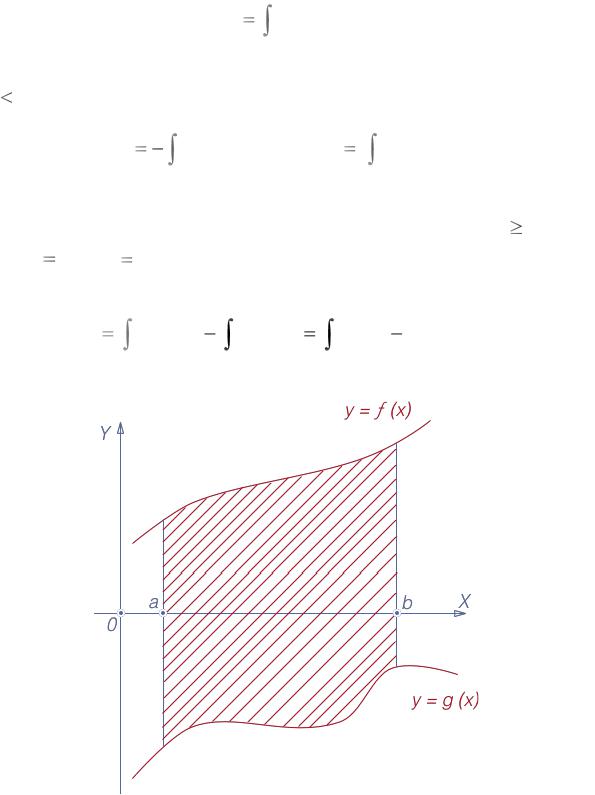
Если фигура ограничена кривыми			f ( x ) и		g( x ) (		где f ( x ) g( x )),
прямыми x a и x	b (см.	рис. 3), то площадь криволинейной трапеции
находится по формуле
b		b		b
S	f x dx	g x dx		f x		g x dx .
a		a		a

Рис. 3

Объем тела вращения

Пусть вокруг оси Ox вращается криволинейная трапеция, ограниченная

непрерывной линией y f ( x )	0, осью Ox и прямыми x a и x b (см.
рис. 4). Объем тела вращения определяется формулой
		b
V		f 2 ( x )dx .
Ox

Если тело образовано вращением криволинейной трапеции вокруг оси Oy , то выражая x через y как обратную функцию, получаем аналогичную формулу для объема тела вращения:

	d
V	x2	( y )dy ,
Oy
	c
где c;d – область изменения функции y		f ( x ).

Рис. 4

2.4.Практическая часть

Пример 1. Воспользуемся правилом интегрирования

f kx b dx	1	F kx b C ,	( )

	k

табличным интегралом 1) и формулой Ньютона-Лейбница, получим:

2	dx	2		1	7	3x	2	2
							2	2

			= 7 3x 3 dx

	7 3x	3		3		2
1	7 3x	1		3		2		1
								1

6 7 3x 2

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.01.20211.22 Mб24613.pdf
#
08.01.20211.22 Mб24614.pdf
#
08.01.20211.22 Mб34615.pdf
#
08.01.20211.23 Mб54616.pdf
#
08.01.20211.23 Mб44618.pdf
#
08.01.20211.23 Mб04619.pdf
#
08.01.2021200.59 Кб1462.pdf
#
08.01.20211.24 Mб24620.pdf
#
08.01.20211.24 Mб54621.pdf
#
08.01.20211.24 Mб44622.pdf
#
08.01.20211.24 Mб24623.pdf