
4610
.pdfФедеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования «Воронежская государственная лесотехническая академия»
М А Т Е М А Т И К А
Преобразование графиков функций
Методические указания и индивидуальные задания для студентов 1 курса всех технических специальностей
Воронеж 2007
2
УДК 517.1
Веневитина, С. С. МАТЕМАТИКА. Преобразование графиков функций [Текст] : методические указания и индивидуальные задания для студентов 1 курса всех технических специальностей / С. С. Веневитина, Е. О. Уточкина ; Фед. агентство по образованию, ГОУ ВПО «ВГЛТА». – Воронеж, 2007. – 32 с.
Печатается по решению редакционно-издательского совета ГОУ ВПО «ВГЛТА»
Рецензент канд. физ.-мат. наук, доц. кафедры математического анализа ВГУ Ю.И. Пастухова
3
I.Понятие функции. Основные свойства функций.
Постоянной величиной называется величина, сохраняющая одно и то же значение. Например, сумма углов треугольника есть постоянная величина, равная 180º; отношение длины окружности к её диаметру равно числу π.
Если величина сохраняет постоянное значение лишь в условиях данного процесса, то в этом случае она называется параметром.
Переменной называется величина, которая может принимать различные числовые значения. Например, температура воздуха в течение суток (месяца); скорость при неравномерном движении; количество студентов, пришедших на лекцию и др.
Перейдём к понятию функции.
Определение. Если каждому значению x множества D ( x D ) ставится в соответствие единственное значение y множества E (y E), то говорят, что на множестве D задана функция y = f (x) .
При этом x называют независимой переменной (или аргументом), y – зависимой переменной, а буква f обозначает закон соответствия.
Множество D(y) называется областью определения функции, а множество E(y) – множеством значений функции.
Если множество D специально не оговорено, то находят естественную область определения функции, т.е. множество таких значений независимой переменной, при которых функция y = f (x) вообще имеет смысл.
Рассмотрим основные свойства функций.
1. |
Чётность и нечётность. Функция |
y = f (x) называется чётной, |
|
если для всех |
x D( y) выполняется равенство |
f (−x) = f (x) . |
|
Область определения чётной функции симметрична относительно |
|||
начала координат ( т.е. если точка |
|
||
a D( y) , то и точка −a D( y) ). |
|
||
График |
чётной функции |
|
|
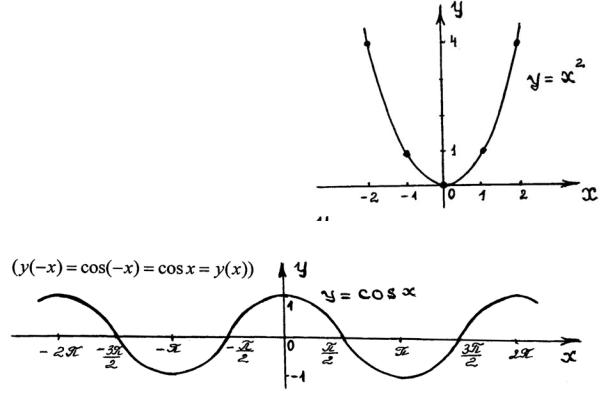
симметричен относительно оси Oy. Примеры чётных функций:
y = x2
(y(−x) = (−x)2 = x2 = y(x))
4
Функция y = f (x) называется нечётной, если для всех x D( y) выполняется равенство f (−x) = − f (x) .
Область определения нечётной функции так же симметрична относительно начала координат.
График нечётной функции симметричен относительно начала координат.
Примеры нечётных функций:
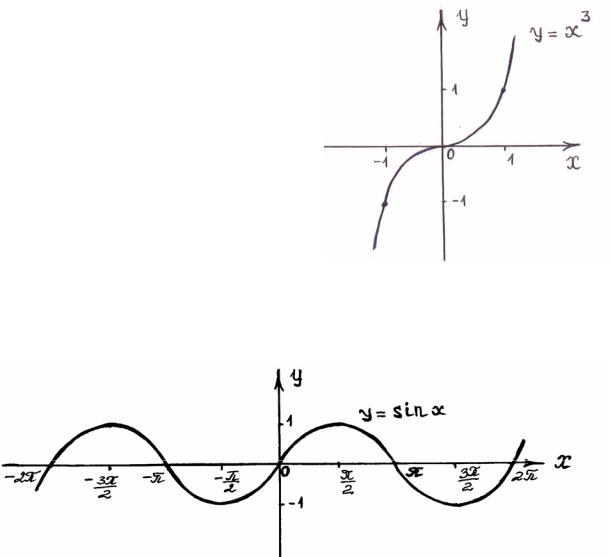
y = x3
( y(−x) = (−x)3 = −x3 = −y(x))
y =sin x
( y(−x) =sin(−x) = −sin x = −y(x))
В случае когда y(−x) ≠ y(x) и y(−x) ≠ −y(x) , |
функция y = f (x) |
называется функцией общего вида ( например, y = x2 + x3 ; |
y = 2 x и т. д. ). |
2.Монотонность. Функция y = f (x) называется возрастающей
(убывающей) на промежутке X , если большему значению аргумента x X соответствует большее (меньшее) значение функции.
5
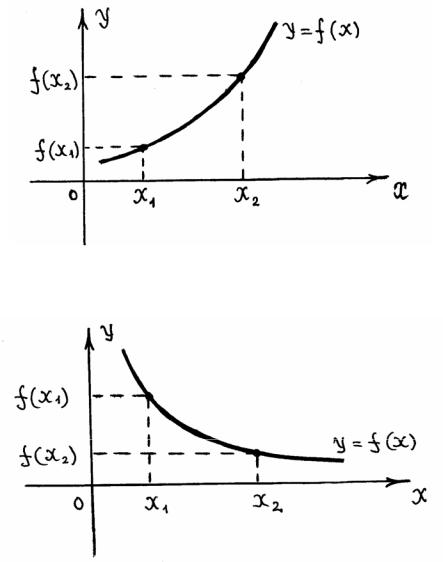
Другими словами, функция y = f (x) возрастает, если для всех x1, x2 D( y) таких, что x1 < x2 выполняется неравенство f (x1 ) < f (x2 ) :
Функция убывает, если для всех x1, x2 D( y) таких, что x1 < x2 выполняется неравенство f (x1 ) > f (x2 ) :
Функция только возрастающая или только убывающая на данном числовом промежутке называется монотонной на этом промежутке.
3. Периодичность. Функция y = f (x) называется периодической, если существует такое число T ≠ 0 , что при любом x D( y) числа x −T и x +T
также принадлежатD( y) и выполняется |
равенство |
f (x) = f (x −T ) = f (x +T ) . |
|
Наименьшее такое число T называется периодом функции f (x) . |
|||
Например, |
функции y = sin x и |
y = cos x |
имеют период T = 2π , а |
функции y =tgx и |
y =ctgx - период T = π . |
|
|
II.Основные элементарные функции.
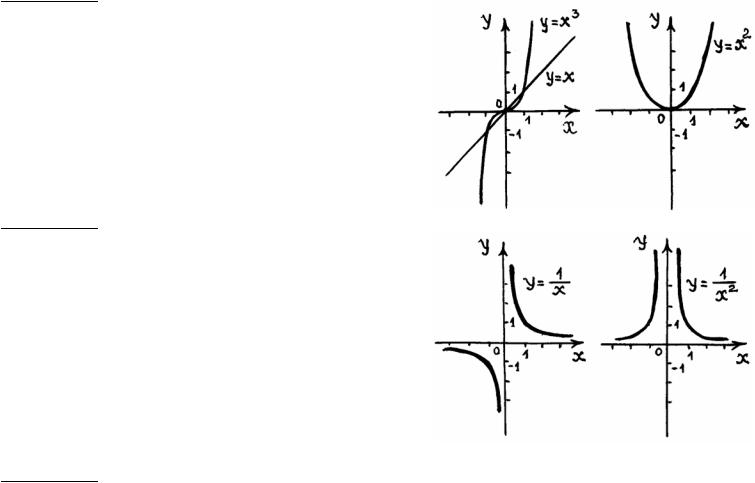
Наиболее важные свойства и графики основных элементарных функций приведём в таблице:
6
№ |
Обозна- |
Область |
Область |
Чётность, |
|
Монотон- |
|
Перио- |
Графики функций |
|||
п/п |
чение |
опреде- |
значений |
нечёт- |
|
|
ность |
|
|
дичность |
|
|
|
функ- |
ления X |
Y |
|
ность |
|
|
|
|
|
|
|
|
ции |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
5 |
|
|
|
6 |
|
7 |
8 |
|
|
|
(−∞;∞), |
|
|
1. |
Степенная функция |
|
||||
1 |
y = xn |
(−∞;∞) |
|
нечётная, |
|
возрастает |
на |
неперио- |
|
|||
|
n N |
|
если |
n - |
если |
n - |
|
(−∞;∞), если |
дическая |
|
||
|
|
|
нечётно; |
нечётно; |
|
n - |
нечётно; |
|
|
|||
|
|
|
[0;∞), |
|
чётная, |
n - |
|
убывает |
на |
|
|
|
|
|
|
если |
n - |
если |
|
(−∞;0] |
и |
|
|
||
|
|
|
чётно |
|
чётно |
|
|
возрастает |
на |
|
|
|
|
|
|
|
|
|
|
|
(0;∞), если n - |
|
|
||
|
|
|
|
|
|
|
|
чётно |
|
|
|
|
|
|
|
(−∞;0) U |
|
|
|
|
|
|
|||
2 |
y = x−n |
(−∞;0) U |
нечётная, |
|
убывает |
на |
неперио- |
|
||||
|
n N |
U(0;∞) |
U(0;∞), ес |
если |
n - |
|
(−∞;0) U |
|
дическая |
|
||
|
|
|
ли |
n - |
нечётно; |
U(0;∞), если |
|
|
|
|||
|
|
|
нечётно; |
чётная, |
n - |
|
n - |
нечётно; |
|
|
||
|
|
|
(0;∞), есл |
если |
|
возрастает |
на |
|
|
|||
|
|
|
и |
n - |
чётно |
|
|
(−∞;0) |
и |
|
|
|
|
|
|
чётно |
|
|
|
|
убывает |
на |
|
|
|
|
|
|
|
|
|
|
|
(0;∞), если n - |
|
|
||
|
|
|
|
|
|
|
|
чётно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7
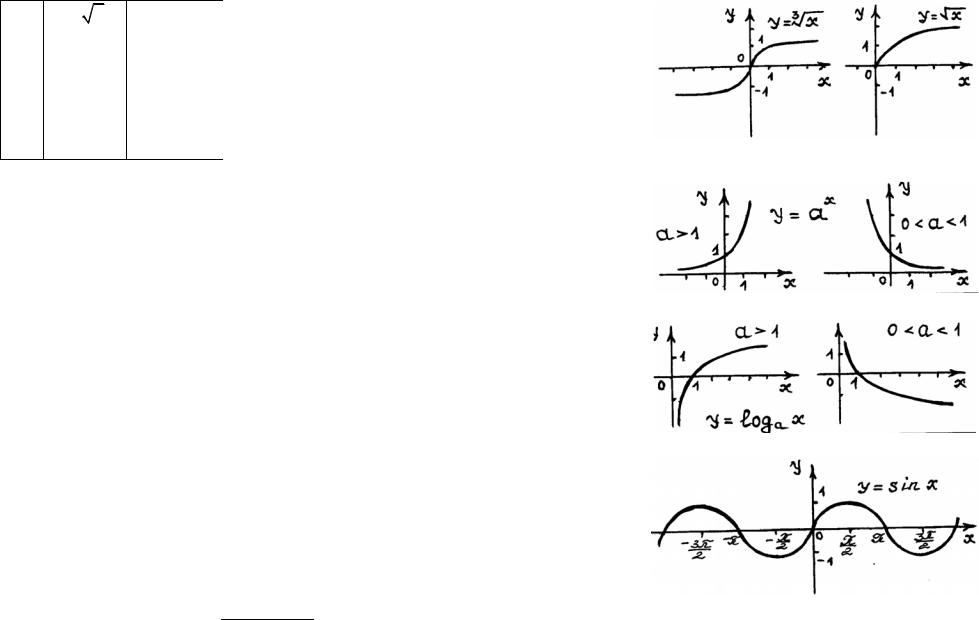
3 y = n x
n N n >1
(−∞;∞), |
|
(−∞;∞), |
|
|
|
|
|
|
|||
|
|
нечётная, |
возрастает |
на |
неперио- |
|
|||||
если |
n - |
|
если |
n - |
если |
n - |
(−∞;∞), если |
дическая |
|
||
нечётно; |
|
нечётно; |
нечётно; |
n - |
нечётно; |
|
|
||||
[0;∞), |
|
|
[0;∞), |
|
общего |
|
возрастает |
на |
|
|
|
если |
n - |
|
если |
n - |
вида, |
n - |
[0;∞), если n - |
|
|
||
чётно |
|
|
чётно |
|
если |
чётно |
|
|
|
|
|
|
|
|
|
|
чётно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4 |
y = ax |
(−∞;∞) |
(0;∞) |
общего |
|
|
возрастает на |
неперио- |
|
||||
|
(a > 0, |
|
|
|
|
вида |
|
|
(−∞;∞), |
если |
дическая |
|
|
|
a ≠1) |
|
|
|
|
|
|
|
a >1, |
убывает |
|
|
|
|
|
|
|
|
|
|
|
на |
(−∞;∞), |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
если 0 < a <1 |
|
|
||
|
|
|
|
|
|
3. |
Логарифмическая функция |
||||||
5 |
y = |
(0;∞) |
(−∞;∞) |
общего |
|
|
возрастает на |
неперио- |
|
||||
|
=loga x |
|
|
|
|
вида |
|
|
(0;∞), |
|
если |
дическая |
|
|
( a >0, |
|
|
|
|
|
|
|
a >1, |
убывает |
|
|
|
|
a ≠1) |
|
|
|
|
|
|
|
на (0;∞), |
если |
|
|
|
|
|
|
|
|
|
|
|
0 < a <1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
[−1;1] |
|
4. Тригонометрические функции |
|||||||
6 |
y =sin x |
(−∞;∞) |
|
|
нечётная |
|
|
возрастает на |
период |
|
|||
|
|
|
|
|
|
|
|
|
[−π / 2 + 2πn; |
T = 2π |
|
||
|
|
|
|
|
|
|
|
|
π / 2 + 2πn]; |
|
|
||
|
|
|
|
|
|
|
|
|
убывает на |
|
|
||
|
|
|
|
|
|
|
|
|
[π / 2 + 2πn; |
|
|
||
|
|
|
|
|
|
|
|
|
3π / 2 + 2πn], |
|
|
||
|
|
|
|
|
|
|
|
|
n Z |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
[−1;1] |
|
|
|
|
||
7 |
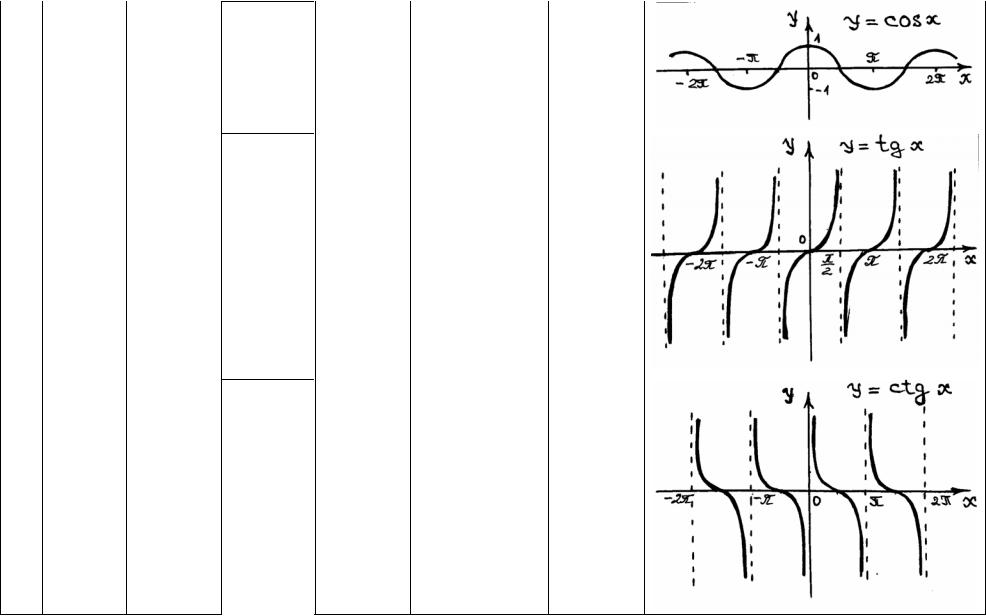
y = cos x (−∞;∞) |
чётная |
возрастает |
на |
период |
|||
|
|
|
|
|
[−π + 2πn;2πn] |
T |
= π |
|
|
|
|
|
|
убывает |
на |
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
[2πn,π + 2πn], |
|
|
|
|
|
|
|
|
n Z |
|
|
|
|
|
|
(−∞;∞) |
|
|
|
|
|
8 |
y =tgx |
π |
нечётная |
возрастает |
на |
период |
||
|
(− |
2 +πn; |
|
|
(−π / 2 +πn; |
|
T =π |
|
|
π |
+πn), |
|
|
π / 2 +πn), |
|
|
|
|
2 |
|
|
n Z |
|
|
|
|
|
n Z |
|
|
|
|
|
|
|
|
(−∞;∞) |
|
|
9 y = ctgx (πn; |
нечётная убывает |
на период |
|
π +πn), |
|
(πn;π +πn), |
T =π |
n Z |
|
n Z |
|
9
III. Преобразование графиков функций.
Для исследования и построения графиков функций можно применять методы математического анализа, теорию пределов, дифференциальное исчисление. Вместе с тем актуальными остаются приёмы построения графиков функций с помощью преобразования графиков основных элементарных функций.
Пусть задан график функции y = f (x) и произвольные положительные
константы a, b, m и k. Тогда справедливы следующие правила.
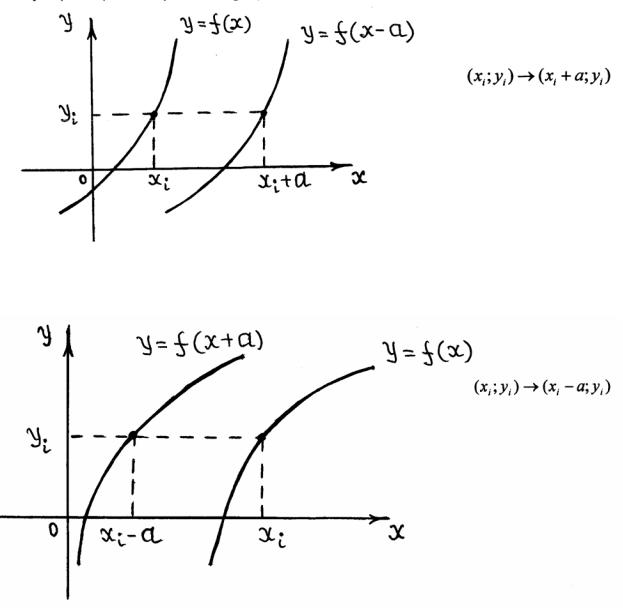
Правило 1. График функции y = f (x −a) получается из графика функции y = f (x) сдвигом вдоль оси Ox на a единиц вправо.
Таким образом, каждая точка (xi ; yi ) исходного графика переходит в точку (xi + a; yi ) ,и получается график новой функции.
График функции |
y = f (x + a) получается из графика функции |
y = f (x) сдвигом вдоль оси Ox на a единиц влево.
Правило 2. График функции y = f (x) +b получается из графика функции y = f (x) сдвигом вдоль оси Oy на b единиц вверх.

10
График функции y = f (x) −b получается из графика функции y = f (x) сдвигом вдоль оси Oy на b единиц вниз.
Правило 3. |
График функции y = mf |
(x) получается из графика |
функции y = f (x) растяжением в m раз вдоль оси |
Oy , если m>1. |
|
Если же m (0;1) , то график функции y = mf (x) получается из графика функции y = f (x) сжатием в m1 раз вдоль оси Oy.
Правило 4. График функции y = f (kx) получается из графика функции y = f (x) сжатием в k раз вдоль оси Ox, при k>1.
