4562

11

Задание

1.Определить оценку дисперсии S2, используя даны работы 1 и 2.

2.Определить величину t из табл. 1 приложения.

3.Определить необходимый объем выборки.

Контрольные вопросы

1.Дайте определение случайной величины.

2.Назовите основные статистические характеристики случайных величин и их вычисления.

3.Дайте определение математического ожидания.

4.От чего зависит максимальная ошибка?

5.Как определить необходимый объем выборки?

Варианты заданий

Опыт 1. В ходе проведения экспериментальных исследований получены данные по количеству поросли осины на вырубках различного возраста.

Таблица 2.1 – Количество поросли осины на вырубках

Опыт 2. В ходе проведения экспериментальных исследований при распиловке древесины на круглопильных станках были получены значения удельной работы резания К, МДж/м3.

Таблица 2.2 – Значения удельной работы резания К, МДж/м3

Значения К, МДж/м3

12

Лабораторная работа №3 Применение методов интерполяции и экстраполяции для анализа резуль-

татов эксперимента

Цель работы изучение методов линейной интерполяции и экстраполяции и при анализе результатов экспериментальных исследований.

Ход выполнения работы

Выполнение экспериментов связано с изучением влияния различных воздействий (факторов) на объект исследования. Факторы (x), действующие на объект, изменяют его состояние. По величине отклика (y) судят об изменении состояния объекта. В результате выполнения опытов, в которых изучаемые факторы (x) варьируются на определенных заданных уровнях x1, x2 … xn, могут быть получены выходные значения с величиной отклика y1, y2 … yn соответственно. Записанные в таблицы в необходимой последовательности парные значения факторов xi и откликов yi представляют функцию вида y (x) , выраженную с помощью ее численных значений.

Большим удобством табличного способа задания функции является то, что значения функции уже вычислены для соответствующих аргументов. Однако при табличном способе задания функции она определяется дискретно, только в точках аргумента, называемых узлами (x1; x2; … xn), интервал между которыми называется шагом (h):

h1=x2-x1; h2= x3-x2; … hn-1=xn-xn-1.

Однако нередко для детального анализа результатов исследований требуется знать значение функции для аргументов, значений которых нет в таблице. Тогда приходится производить дополнительные вычисления:

интерполяцию (для значений аргументов, лежащих в промежутке двух соседних факторов xi 1 xi );

экстраполяцию (для значений аргументов, лежащих за пределами изучаемых факторов).

Метод линейной интерполяции

Интерполяция заключается в нахождении значений функции y f (x) , заданной n узлами, в промежутки между этими узлами.

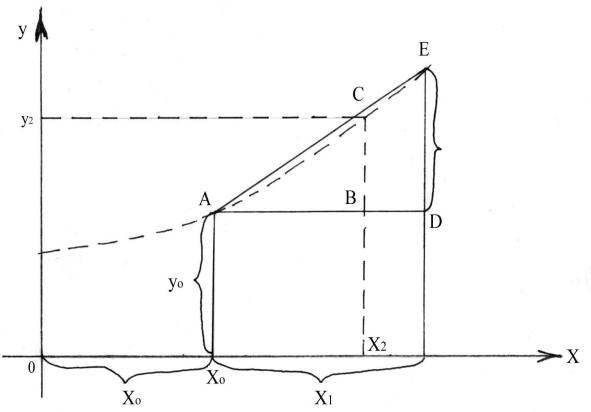
Рассмотрим метод линейной интерполяции на примере некоторой функции y f (x) , график которой изображен на рис. 3.1.

13

Рисунок 3.1 – Схема линейной интерполяции

Пусть для этой функции известны ее табличные значения f (x0 ) y0 и f (x0 h) y , в двух соседних узлах x0 и x1= x0+h, но неизвестны при промежуточном значении x2, где x0 <x2< x1.

Линейную интерполяцию проводят, используя формулу

где h – шаг между соседними узлами.

Метод линейной экстраполяции

Экстраполяция заключается в нахождении функции y=f(x) для значений аргументов, лежащих за пределами факторов, задействованных в эксперименте. Пусть для функции y=f(x) известны ее табличные значения f(x0)=y0 и f(x0+h)=y1 в двух соседних узлах при x0 и x1= x0+h и неизвестны при x0>x2>x1, (x0<x2<x1).

Как видно из рис. 3.2., линейную экстраполяцию производим по той же формуле (3.1), что и линейную интерполяцию.

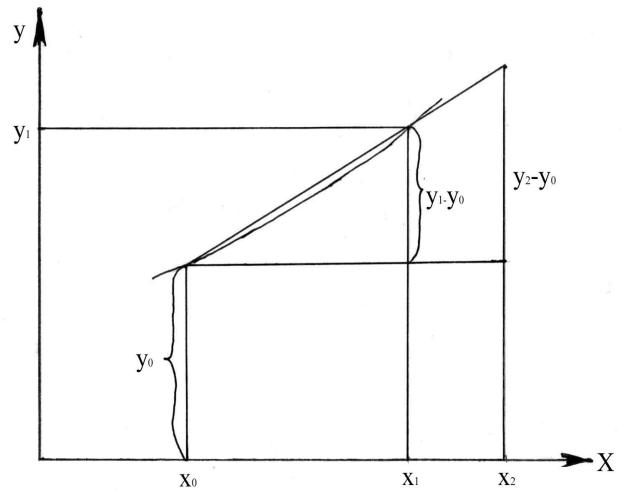
14

Рисунок 3.2 – Схема линейной экстраполяции Данные, используемые для интерполяции, получают по результатам вы-

полненных лабораторных работ или научных исследований, проводимых в лабораторных или полевых условиях. Полученные данные должны включать значения: x0, y0, x1, y1 и т.д.

Задание

1.Определить шаг между соседними узлами.

2.Провести линейную интерполяцию (экстраполяцию) экспериментальных данных.

Варианты заданий

Опыт 3. При исследовании механизма подачи рейсмусового станка получено 15 замеров остаточной деформации древесины стальным вальцом в статике и в динамике – соответственно xi и yi

Опыт 5. Определить высоту ординаты 6 и 12 Таблица 3.2

Контрольные вопросы

1.Что понимается под корреляционной связью?

2.В чем суть корреляционного анализа?

3.Как определяют табличное значение t-критерия Стьюдента?

4.Что такое уровень значимости?

5.Как проводится оценка статистической связи случайных величин?

6.Что такое линейная интерполяция?

7.Порядок определения промежуточных значений функции.

8.Общее понятие экстраполяции.

9.Порядок нахождения значений функции за пределами ее табличных значений.

16

Лабораторная работа №4 Сглаживание эмпирических данных с ошибками

Цель работы – ознакомиться с методом сглаживания экспериментальных данных с ошибками и получить навыки применения при проведении научных исследований.

Ход выполнения работы

В случае, когда экспериментальные данные, по которым реализуются табличные значения функции ỹ = f (x) , содержат случайные ошибки, проводят их сглаживание. Наибольшее применение для выравнивания экспериментальных данных, полученных при постоянном шаге (h) аргумента (xi) , имеет способ наименьших квадратов.

По этому способу сглаженные значения неплавной функции определяются из выражения

где y-2; y-1;y0;y1 и y2 – пять последних значений функции из несглаженной таблицы;

уос – есть сглаженное значение у0, которым его заменяют.

Достоинство этого способа – его точность, особенно для параболических зависимостей. Недостаток – отсутствие сглаживания двух первых и двух последних точек, поэтому сглаживание по способу наименьших квадратов применимо лишь при количестве узлов (точек).

Для практических целей наиболее удобными считаются интерполяционные методы выравнивания экспериментальных данных по трем или пяти координатам (узлам).

Например, достаточно высокую точность приближения получают при использовании линейного интерполяционного сглаживания по трем ординатам. При этом расчетные значения сглаживаемых величин определяется по формулам:

где y0; y1;……yn – экспериментальные значения ординат; ỹ0; ỹ1; …...ỹn – сглаженные значения ординат.

Сгладим по этому способу данные третьего столбца таблицы.

17

Вычисления ведем с верхней части столбца. Тогда у-2=1,0; у-1=1,6; у0=1,8;

у1=2,3; у2=1,8.

Для степени затупления лемеха получаем

уос 351 17 1,8 12 2,3 1,6 3 1,8 1,0 1,97 .

Соответственно для следующих степеней затупления:

уос 351 17 2,3 12 1,8 1,8 3 2,4 1,6 2,01; уос 351 17 1,8 12 2,4 2,3 3 2,5 1,8 2,12 ;

уос 351 17 2,4 12 2,5 1,8 3 2,7 2,3 2,21.

Следовательно, получили сглаженный по способу наименьших квадратов ряд точек средних квадратических отклонений глубины вспашки: 1,0; 1,6; 1,97;

2,01; 2,12; 2,21; 2,5; 2,7.

Как видно, сглаживание «скользит» вдоль рядов таблицы, причем выбор начала сглаживания зависит от того, какие две краевые точки ряда исследователь считает наиболее правильными, с них и начинают сглаживание.

В формуле (4.1) приведено пять значений функции для сглаживания, что дает, по нашему мнению, достаточно правильные результаты. Подобные формулы имеются и для другого числа значений функции, но меньшее число увеличивает ошибку, а большее оставляет по краям таблицы слишком много несглаженных результатов, что также увеличивает ошибку. Поэтому для многих исследований способ, представленный формулой (4.1), близок к оптимальному. В некоторых случаях его приходится применять не для всех точек, а лишь для некоторых их групп.

При многократном сглаживании математическими методами может возникнуть ошибка. Так, например, если кривую, по физическому смыслу гиперболическую, неоднократно сглаживать параболическими приближениями, то эта кривая становится близкой к параболе. Чтобы этого не случилось (или случилось в наименьшей степени), следует после каждого сглаживания ряда брать сумму квадратов отклонения найденных сглаженных значений функции от опытных точек. Наименьшая сумма квадратов отклонений будет соответствовать оптимальному сглаживанию.

18

Задание

1. Произвести сглаживание эмпирических данных с ошибками

Варианты заданий

Опыт 1. На лесосеке были проведены наблюдения за работой валочнопакетирующей машины. При этом определялись следующие пары величин: объем спиливаемого дерева qхл и время цикла валки-пакетирования tц одного дерева. Определить корреляционную связь.

Таблица 4.1

Контрольные вопросы

1.Порядок нахождения значений функции за пределами ее табличных значений.

2.Дать определение промаха измеряемой величины и пояснить порядок ее выбраковки.

3.Какими способами осуществляется сглаживание экспериментальных данных?

19

Лабораторная работа №5 Составление уравнения регрессии первого порядка методом наи-

меньших квадратов

Цель работы – научиться определять коэффициенты и составлять уравнения регрессии первого порядка по результатам обработки экспериментальных данных с использованием метода наименьших квадратов.

Ход выполнения работы

В процессе экспериментальных измерений получают статистический ряд измерений двух величин, которые объединены функцией y = f (x), здесь каждому значению функции y1, y2, …, yn соответствует определенное значение аргумента x1, x2, … , хп.

На основании экспериментальных данных можно подобрать алгебраические выражения, которые называются эмпирическими формулами. Такие формулы подбирают лишь в пределах измеренных значений аргумента. Эмпирические формулы имеют тем большую ценность, чем больше они соответствуют результатам эксперимента. Подбор эмпирических формул необходим в случаях, если аналитическое выражение сложное, требует громоздких вычислений, составления программ на ЭВМ и т. д. Опыт показывает, что эмпирические формулы часто незаменимы для анализа измеренных величин. К эмпирическим формулам предъявляют два основных требования:

1)по возможности, они должны быть наиболее простыми;

2)точно соответствовать экспериментальным данным в пределах изменения аргумента.

Поэтому эмпирические формулы являются приближенными выражениями аналитических формул. Замена точных аналитических выражений приближенными, более простыми, называют аппроксимацией, а функции аппроксимирующими.

Процесс подбора эмпирических формул состоит из двух этапов:

1. Данные измерений наносят на сетку координат, соединяют точки плавной кривой и выбирают ориентировочно вид формулы.

2. Вычисляют параметры формул (коэффициенты), которые наилучшим образом соответствовали бы принятой формуле. Подбор эмпирических формул необходимо начинать с самых простых выражений.

20

Врезультате выполнения экспериментальных исследований интересующая нас функция обычно оказывается заданной в табличном виде, когда значениям аргумента (варьируемым факторам) x1 ;x2 ;…xn соответствуют конкретные значения функции отклика y1 ;y2 ;…yn . Для получения аналитического выражения, являющегося функцией отклика, проводят регрессионный анализ, позволяющий получить уравнение регрессии в виде приближенной эмпирической формулы, с помощью которой можно с заданной точностью оценить степень и характер влияния каждого из факторов на выходную величину.

Переход от табличных экспериментальных данных к аналитическим зависимостям может осуществляться различными способами. Наиболее распространенный из них является метод наименьших квадратов.

При пользовании этим методом обычно предварительными исследованиями определяют предполагаемый вид искомой функции y = f (x).

Далее находят основные параметры аналитической функции, которая с минимальной погрешностью приближалась бы к исходной функции y = f (x). Такому условию в наилучшей степени отвечает требование, при которых сумма квадратов отклонений ΣΔh2i откликов (y1 ;y2 ;…yn) от линий функции y = f (x) была бы минимальной. Указанный метод и получил наименование метода наименьших квадратов. С его помощью могут быть определены коэффициенты уравнений регрессии линейного, параболического, степенного, гиперболического, экспоненциального и т.п. видов.

Вцелом ряде случаев сущность полученных в результате экспериментов функциональных зависимостей оказывается неизвестной, в результате чего никаких предварительных предположений об общем виде уравнений сделать бывает невозможно. В таких случаях приходится ограничиваться подбором наиболее простых формул, результаты вычислений по которым ближе всего подходят к обоснованию функциональных связей экспериментальных данных.

На первых этапах исследований чаще всего обращаются к регрессионным моделям первого порядка, линейным уравнениям вида

где b0 и b1 – коэффициенты линейного приближения, определяемые по формулам: