
4499
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ЛЕСОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ИМЕНИ Г.Ф. МОРОЗОВА»
ЛИНЕЙНАЯ АЛГЕБРА
Методические указания для самостоятельной работы студентов
по направлению подготовки 38.03.01 – Экономика
Воронеж 2016
3
УДК 512.8
Раецкая, Е. В. Линейная алгебра [Текст] : методические указания к практическим занятиям для студентов по направлению подготовки 38.03.01 – Экономика / Е. В. Раецкая, И.В. Сапронов, Н.М. Спирина ; М-во образования и науки РФ, ФГБОУ ВО «ВГЛТУ». – Воронеж, 2016. – 46 с.
Печатается по решению учебно-методического совета ФГБОУ ВО «ВГЛТУ» (протокол № 5 от 22 апреля 2016 г.)
|
Рецензент д-р физ.-мат. наук, доцента кафедры математического анализа |
ВГУ |
Зубова С.П. |
4
Содержание Введение……………………………………………………………………………4 1.Матрицы и определители………………………………………………………5
2.Системы линейных уравнений………………………………………………10
3.Векторная алгебра……………………………………………………………..15
4.Аналитическая геометрия…………………………………………………….28
5.Кривые второго порядка……………………………………………………..36
Вопросы для контроля. ………………………………………………………….44
Библиографический список…………………………………………………...45
5
Введение
Целью изучения дисциплины «Линейная алгебра» является воспитание достаточно высокой математической культуры, привитие навыков современных видов математического мышления, обучение основным математическим понятиям и методам линейной алгебры, необходимым для анализа и моделирования устройств, процессов и явлений при поиске оптимальных решений практических задач, методам обработки и анализа результатов численных экспериментов для экономических задач.
Для достижения поставленной цели, при самостоятельной работе решаются следующие задачи:
-самостоятельное усвоение студентом теоретического материала, построенного на основе четких формулировок и доказательстве основных теорем и выработка умения самостоятельно иллюстрировать его примерами и задачами; самостоятельное изучение истории появления наиболее важных понятий и результатов; наряду с изучением основных теоретических результатов при самостоятельной работе с учебными материалами, необходимо обращать внимание на пояснения об их приложениях к другим разделам математики и к техническим наукам;
-закрепление теоретического материала и выработка умения самостоятельно применять математические методы в различных приложениях.
Врезультате самостоятельного освоения дисциплины студент должен:
-знать основные понятия, определения и методы исследования объектов с помощью теорем и формул различных разделов курса математики;
-уметь: четко формулировать и доказывать основные положения курса математики, решать задачи и примеры по различным разделам высшей математики с доведением решения до практического приемлемого результата (формулы, числа, графика, качественного вывода и т.п.), уметь при решении задач самостоятельно выбирать необходимые вычислительные методы и средства (ПЭВМ, таблицы и справочники); самостоятельно изучать научную литературу по математике;
-иметь представление о численных алгоритмах решения математических и прикладных задач его профессиональной области.
Студент по результатам освоения дисциплины «Линейная алгебра» должен обладать способностью выбрать инструментальные средства для обработки экономических данных в соответствии с поставленной задачей, проанализировать результаты расчетов и обосновать полученные выводы.
6
|
|
|
1. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ |
|
Матрицей А размера m n называется таблица из |
m n чисел |
|||
a |
a |
... |
a |
|
11 |
12 |
|
1n |
|
a21 |
a22 |
... |
a2n |
|
A |
|
|
... |
|
... ... |
... |
|
||
|
|
|
|
|
|
am2 |
... |
|
|
am1 |
amn |
|
||
Часто для краткости пишу A 
 aij
aij 
 . Числа, из которых состоит матрица,
. Числа, из которых состоит матрица,
называются элементами матрицы. Индексы у элементов матрицы указывают расположение этого элемента в таблице: первый индекс – номер строки, в которой находится элемент, а второй – номер столбца. Например, элемент a21 находится на пересечении второй строки и первого столбца:
|
a |
a |
... |
a |
|
||
|
|
11 |
|
12 |
|
1n |
|
|
|
|
|
|
|
||
|
a21 |
|
a22 |
... |
a2n |
||
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||
... |
... |
... |
... |
|
|||
|
|
|
am2 |
... |
|
|
|
am1 |
amn |
||||||
Элементы |
a11, a22 , a33 ,... |
называются элементами главной диагонали |
|||||
матрицы или просто главной диагональю матрицы.
Матрица A, состоящая из одной строки называется строкой (векторстрокой), матрица, состоящая из одного столбца называется столбцом (векторстолбец). Матрица, получающаяся из матрицы A заменой строк столбцами называется транспонированной матрицей по отношению к матрице A и обозначается AT , элементы транспонированной матрицы и исходной связаны соотношением aijT a ji .
Если матрица А имеет размер n n , то такую матрицу называют квадратной матрицей порядка n . Две матрицы одинакового размера A 
 aij
aij 

7
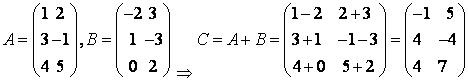
и B |
|
bij |
|
|
называют равными (при этом пишут А = В), если |
aij bij , |
|||||||||||||
i 1,..., m ; |
j 1,...n . |
( т.е., если у них соответственно равны элементы, |
|||||||||||||||||
стоящие на одинаковых местах в таблице). |
|
|
|
|
|
|
|
|
|
|
|||||||||
Суммой двух матриц одинакового размера m n |
A |
|
|
|
и B |
|
bij |
|
|
||||||||||
|
aij |
|
|
|
|
|
|||||||||||||
называют матрицу C |
|
|
размера m n такую, что |
|
|
|
|
|
|
|
|
|
|
||||||
|
cij |
|
|
|
|
|
|
|
|
|
|
|
|||||||
cij aij |
bij , |
i 1,..., m ; j 1,...n . |
|
|
|
|
|
|
|
|
|
|
|||||||
.
Нулевой матрицей 0 называется матрица, все элементы которой равны нулю.
Легко проверить, что выполнены следующие свойства для операции сложения матриц:
1.А+В=В+А (коммутативность),
2.(А+В)+С=А+(В+С) (ассоциативность),
3.А+0=А.
Произведением матрицы размера m n |
A |
|
aij |
|
на число называют |
|||||||||||
|
|
|||||||||||||||
матрицу того же размера |
C |
|
|
|
такую, |
что |
cij |
aij |
i 1,..., m ; |
|||||||
|
cij |
|
|
|||||||||||||
j 1,...n . Умножение |
матрицы |
A |
|
|
|
размера m n на матрицу |
||||||||||
|
aij |
|
|
|||||||||||||
B 
 bij
bij 
 размера
размера  определено лишь для случая, когда число столбцов
определено лишь для случая, когда число столбцов
матрицы А совпадает с числом строк матрицы В, т.е. когда n=l. В этом случае произведение матриц определяется следующим образом:
Произведением матриц АВ называется матрица
8

C |
|
cij |
|
размера |
, у которой |
,
Иначе говоря, элемент cij равен сумме произведений элементов i-ой строки матрицы А на соответствующий элемент j-ого столбца матрицы В. С помощью знака суммирования можно записать это так:
k |
|
|
cij ailblj |
ai1b1 j ai 2b2 j |
aik bkj |
l 1 |
|
|
Единичной матрицей порядка n называется квадратная матрица вида
|
|
1 |
0 |
0 |
|
|
|
0 |
1 |
0 |
|
E |
. |
||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 1 |
|
|
|
|
|||
Каждой квадратной матрице можно сопоставить некоторое число, называемое определителем матрицы и обозначаемое через |A| или A Прежде чем дать общее определение этого понятия, определим его для матриц 2-го и 3-го порядков.
Определителем матрицы 2-го порядка называется число
.
Определителем матрицы 3-го порядка называется число
9

Общее понятие определителя дадим с помощью рекуррентной схемы, а именно, считая, что понятие определителя известно для матриц
п–1-го порядка, дадим его для матриц п-го порядка (фактически так и вводилось понятие определителя для матриц 3-го порядка).Определителем
матрицы A 
 aij
aij 
 порядка п называется число
порядка п называется число
Определитель матрицы A принято обозначать A , или A , или det A.
Основные свойства определителей.
1. Определитель матрицы и транспонированной матрицы не изменяется т.е.
|
a11 |
a12 |
a13 |
|
a11 |
a21 |
a31 |
|
|
a21 |
a22 |
a23 |
|
a12 |
a22 |
a32 |
|
|
a31 |
a32 |
a33 |
|
a13 |
a23 |
a33 |
|
2. Общий |
множитель в |
строке или столбце можно вынести за знак |
||||||
определителя, т.е.
ka11 |
ka12 |
ka13 |
|
a11 |
a12 |
a13 |
a21 |
a22 |
a23 |
k |
a21 |
a22 |
a23 |
a31 |
a32 |
a33 |
|
a31 |
a32 |
a33 |
3. Определитель, имеющий нулевую строку или нулевой столбец, равен нулю:
a11 |
a12 |
a13 |
|
0 |
0 |
0 |
0 |
a31 |
a32 |
a33 |
|
4. Определитель, имеющий две равные строки или два равных столбца, равен нулю:
a11 a12 a13
a11 a12 a13 0 a31 a32 a33
10

5. Определитель, две строки или два столбца которого пропорциональны, равен нулю:
a11 |
a12 |
a13 |
|
ka11 |
ka12 |
ka13 |
0 |
a31 |
a32 |
a33 |
|
6. При перестановке двух строк или двух столбцов определителя он умножается на –1:
|
a11 |
a12 |
a13 |
|
a21 |
a22 |
a23 |
|
|
|
|
|
|
|
|
|
|||
|
a21 |
a22 |
a23 |
|
a11 |
a12 |
a13 |
|
|
|
|
|
|
|
|
|
|||
|
a31 |
a32 |
a33 |
|
a31 |
a32 |
a33 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
b1 c1 |
b2 c2 |
b3 c3 |
|
|
|
|
b1 |
b2 |
b3 |
|
c1 |
c2 |
c3 |
|||
|
|
|
|
|
|
|
|||||||||||||
7. |
|
|
a21 |
a22 |
|
a23 |
|
|
|
a21 |
a22 |
a23 |
|
a21 |
a22 |
a23 |
|||
|
|
|
|
a31 |
a32 |
|
a33 |
|
|
|
|
a31 |
a32 |
a33 |
|
a31 |
a32 |
a33 |
|
8. Величина определителя не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число:
a11 |
a12 |
a13 |
|
a11 ka21 |
a12 ka22 |
a13 ka23 |
|
||||||
a21 |
a22 |
a23 |
|
a21 |
a22 |
a23 |
a31 |
a32 |
a33 |
|
a31 |
a32 |
a33 |
Квадратная матрица называется невырожденной, если ее определитель отличен от нуля. Пусть дана матрица
Выберем k строк и k столбцов в этой матрице и составим новую матрицу из элементов, стоящих на пересечении этих строк и столбцов. Определитель полученной матрицы называется минором порядка k. Например, если выбрать вторую и третью строки, первый и третий столбец, то получим минор второго порядка
11
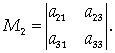
Рангом матрицы называется максимальный порядок ее миноров, отличных от нуля.
Алгебраическим дополнением Aij элемента определителя называется его минор, если сумма индексов данного элемента i j есть число четное, или число, противоположное минору, если i j нечетно, т.е. Aij ( 1)i j
~
Обозначим через A матрицу, составленную из алгебраических дополнений матрицы A .
Квадратная матрица B называется обратной к квадратной матрице A того же порядка, если AB BA E . При этом B обозначается A 1 .
Для существования обратной матрицы необходимо и достаточно, чтобы исходная матрица была невырожденной. Тогда
|
|
|
|
|
|
|
|
|
|
A |
A ... |
|
|
|
|
|
|
|
|
|
|
11 |
21 |
|
1 |
|
1 |
~T |
|
1 |
A12 |
A22 ... |
|||
A |
|
|
|
|
A |
|
|
|
... ... ... |
||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
A |
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
A1n |
A2n ... |
|
|
|
|
|
|
|
|
|
|
||
An1 An2
...
Ann
|
|
|
A |
|||
|
|
|
11 |
|||
|
|
A |
||||
|
|
|||||
|
|
A12 |
||||
|
|
|||||
|
|
|
A |
|||
|
||||||
|
||||||
|
|
|
||||
|
... |
|||||
|
|
|||||
|
|
|
A1n |
|||
|
|
|
|
A |
||
|
|
|
||||
A |
|
|
|
|
A |
|
|
|
21 |
... |
|
n1 |
|
|
|
||
A |
A |
|
||||||
|
|
|
|
|
|
|
||
A |
|
|
|
|
A |
|
|
|
22 |
... |
|
n2 |
|
|
|
||
|
|
|
|
, |
||||
A |
|
|
|
|
A |
|
|
|
... ... |
|
... |
|
|
|
|||
A2n |
|
|
... |
|
Ann |
|
||
|
|
|
|
|
|
|
||
A |
|
|
|
|
A |
|
||
то есть ее элементами являются алгебраические дополнения к элементам транспонированной матрицы A , деленные на ее определитель. Отметим, что обратная матрица A 1 определена однозначно т.е. существует только одна обратная матрица для заданной квадратной невырожденной матрицы
2. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Линейным алгебраическим уравнением называется уравнение вида a1x1 a2 x2 ... an xn b,
где ai и b – числа, xi - неизвестные.
12
