
4360
.pdf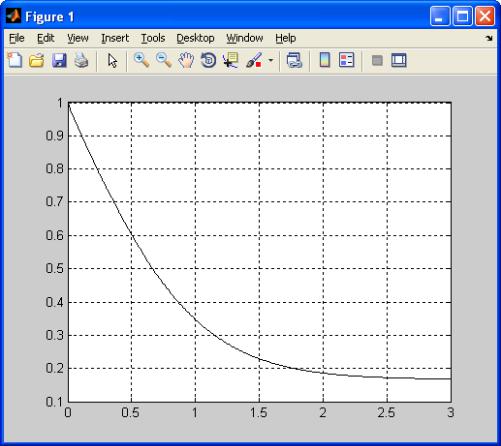
21
Рисунок 3.4 График функции y(t) |
7 |
e 4t |
8 |
e 3t 5te 3t |
1 |
|
|||
|
|
6 |
|
||||||
|
2 |
|
|
3 |
|
||||
Задача 3.4. Найти решение неоднородного дифференциального уравне- |
|||||||||
ния |
|
|
|
|
|
|
|
|
|
|
2y 24y 72y e 2t |
|
|
|
|
|
|||
при начальных условиях |
y(0) 2, y(0) 3 |
c |
использованием |
|
системы |
||||
|
|
|
|
|
|
|
|
||
MATLAB. Написать программу для построения графика полученной функции в
MATLAB.
Решение в MATLAB. Решение неоднородного дифференциального уравнения в символьном виде имеет следующий вид:
>> y=dsolve('2*D2y+24*Dy+72*y=exp(-2*t)','y(0)=2','Dy(0)=3')
y = 63/(32*exp(6*t))+t/(8*exp(2*t))+(119*t)/(8*exp(6*t))-(4*t-1)/ (32*exp(2*t))
>> y=simplify(y)
y = 1/(32*exp(2*t)) + 63/(32*exp(6*t)) + (119*t)/(8*exp(6*t))
Для |
построения |
графика |
полученной |
функции |
y(t) 0,125[0,25e 2t (15,75 119t)e 6t ] необходимо ввести |
короткую про- |
|||
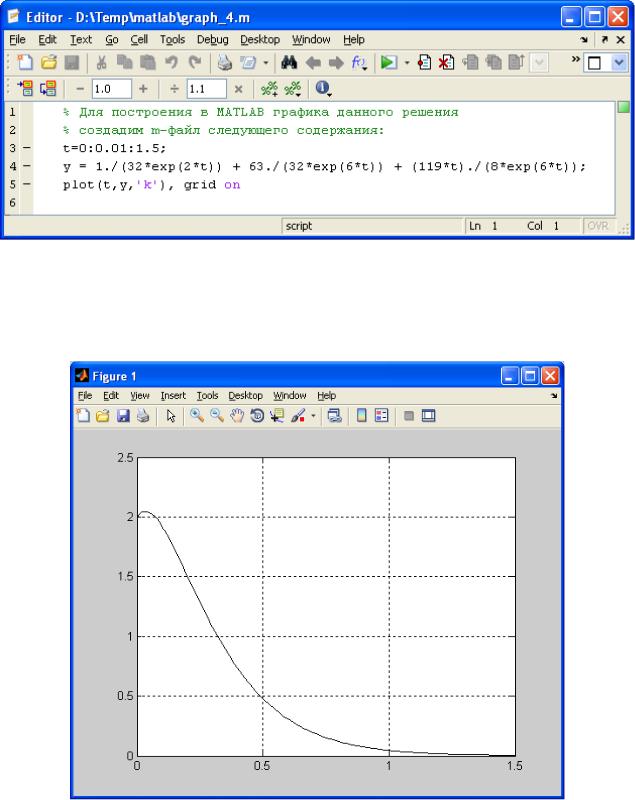
грамму, представленную на рисунке 3.5.
22
Рисунок 3.5 Программа для вывода графика функции y(t) 0,125[0,25e 2t (15,75 119t)e 6t ]
После запуска программы на экране в специальном окне (рисунок 3.6) отображается график функции y(t) 0,125[0,25e 2t (15,75 119t)e 6t ] .
Рисунок 3.6 График функции y(t) 0,125[0,25e 2t (15,75 119t)e 6t ]
3.3. Индивидуальные задания по лабораторной работе
Задача 1. Найти решение однородного дифференциального уравнения
2y 16y 30y 0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
|
|
|
|
|
|
|
при |
начальных |
условиях |
|
|
y(0) 0, y(0) 4 |
c |
использованием |
системы |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MATLAB. Написать программу для построения графика полученной функции в |
|||||||||||||||||||||
MATLAB. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: y(t) 2 e 3t |
2 e 5t . |
|
|
|
|
|
|
|
|
|||||||||||
|
Задача 2. Найти решение неоднородного дифференциального уравнения |
||||||||||||||||||||
|
|
|
|
|
|
|
|
3y 9y 14y 2 3t |
|
|
|
|
|||||||||
при |
начальных |
условиях |
|
y(0) 1, y(0) 1 |
|
c |
использованием |
системы |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MATLAB. Написать программу для построения графика полученной функции в |
|||||||||||||||||||||
MATLAB. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
41 |
|
|
|
|
|
|
|
|
|
||
|
Ответ: y(t) |
|
t e 1,5t |
|
|
sin1,5t cos1,5t . |
|
|
|||||||||||||
|
9 |
27 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Задача 3. Найти решение неоднородного дифференциального уравнения |
||||||||||||||||||||
|
|
|
|
|
|
|
5y 25y 75y 2 e t |
|
|
|
|
||||||||||
при |
начальных |
условиях |
|
y(0) 3, y(0) 1 |
|
c |
использованием |
системы |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MATLAB. Написать программу для построения графика полученной функции в |
|||||||||||||||||||||
MATLAB. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
8 |
|
|
4 |
|
e t |
|
1 |
e 2,5t |
|
76931 |
|
|
||||
|
Ответ: y(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 3t 40571cos 3t . |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
5 |
|
61 |
|
45 |
|
|
|
|
2745 |
|
|
2 |
|
|
|
|
||
3.4. Контрольные вопросы к лабораторной работе
1. Для какой цели используются обыкновенные дифференциальные уравнения в теории автоматического управления?
2.Что называется характеристическим уравнением системы (объекта)?
3.Как используются характеристические уравнения для решения обыкновенных дифференциальных уравнений?
4.Что является решением обыкновенного дифференциального уравне-
ния?
5.Как выполняется решение неоднородных обыкновенных дифференциальных уравнений в системе MATLAB?
24
Лабораторная работа №4. Решение разностных уравнений рекуррентным методом и методом z-преобразования в системе MATLAB (4 часа)
Цель работы: Получение навыков решения разностных уравнений рекуррентным методом и методом z-преобразования в сис-
теме MATLAB.
4.1 Решение разностных уравнений рекуррентным методом
Простейшим способом решения разностных уравнений является рекуррентный метод, позволяющий получить выражение для yk через предыдущие
значения решения yk 1 , yk 2 , … и значение входного воздействия. Затем, ис-
пользуя полученное рекуррентное выражение, можно последовательно вычислять значения решения.
Задача 1. Найти первые пять значений решения разностного уравнения
|
|
yk 1,5yk 1 |
0,6yk 2 |
gk , |
(4.1) |
|||
при g |
k |
0,1k и начальных условиях |
y |
1 |
1, y |
2 |
0,5 . |
|
|
|
|
|
|
|
|||
Решение. Выразим значение |
yk |
|
через предыдущие значения решения |
|||||
yk 1 , |
yk 2 и значение входного воздействия gk . С учѐтом того, что |
gk 0,1k , |
||||||
из уравнения (4.1) получим следующее равенство: |
|
|
||||||
|
|
yk 1,5yk 1 |
0,6yk 2 0,1k . |
(4.2) |
||||
Отсюда при k 0 находим |
|
|
|
|
|
|
||
y0 1,5y 1 0,6y 2 0,1 0 1,5 1- 0,6 0,5 -1,8 .
Аналогично по рекуррентной формуле (4.2) находим значения решения при
k 1 |
y1 1,5y0 |
0,6y 1 |
0,1 1 1,5 1,8 - 0,6 1 0,1 1 2,2 ; |
||
k 2 |
y2 1,5y1 |
0,6y0 |
0,1 2 1,5 2,2 0,6 1,8 0,1 2 2,02 ; |
||
k 3 |
y3 |
1,5y2 |
0,6y1 |
0,1 3 1,5 2,02 |
0,6 2,2 0,1 3 2,01; |
k 4 |
y4 |
1,5y3 |
0,6y2 |
0,1 4 1,5 2,01 |
0,6 2,02 0,1 4 1,403 ; |
k 5 |
y5 1,5y4 0,6y3 0,1 5 1,5 1,403 0,6 2,01 0,1 5 1,3985 . |
||||
Решение в MATLAB:
%Задать начальные значения yk_2=0.5; yk_1=1;
%Создать вспомогательные массивы g=[]; y=[]; kmax=5;
%Организовать цикл
i=0:kmax; for k=i
gk=0.1*k; g=[g;gk]; yk=-0.6*yk_2-1.5*yk_1+gk; y=[y;yk];
|
|
|
25 |
yk_2=yk_1; yk_1=yk; |
|
||
end |
|
|
|
disp(' |
k |
gk |
yk') |
disp([i' g y]) |
|
|
|
plot(i', g, 'o--', i', |
y, 'o--'), grid on |
||
k |
|
gk |
yk |
0 |
|
0 |
-1.8000 |
1.0000 |
|
0.1000 |
2.2000 |
2.0000 |
|
0.2000 |
-2.0200 |
3.0000 |
|
0.3000 |
2.0100 |
4.0000 |
|
0.4000 |
-1.4030 |
5.0000 |
|
0.5000 |
1.3985 |
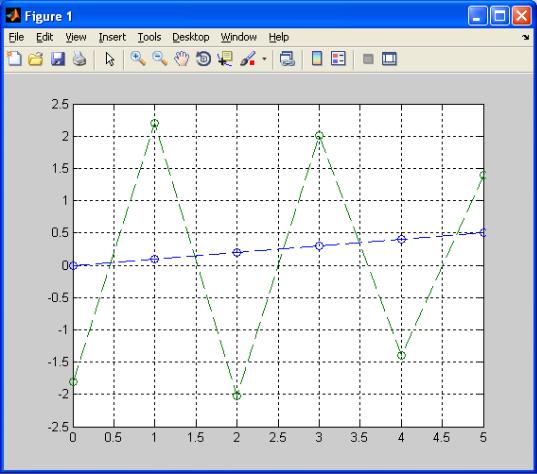
На графике, показанном на рисунке 4.1, приведены значения функции gk 0,1k и найденные начальные значения решения yk . Следует отметить,
что решениями разностных уравнений являются дискретные (решѐтчатые) функции. Именно их значения соединены отрезками, показанными на рисунке 4.1. Их приводят, чтобы подчеркнуть, сделать более наглядным характер (монотонный или колебательный) соответствующих дискретных функций.
Рисунок 4.1 Начальные значения решение разностного уравнения yk и его правой части gk
26
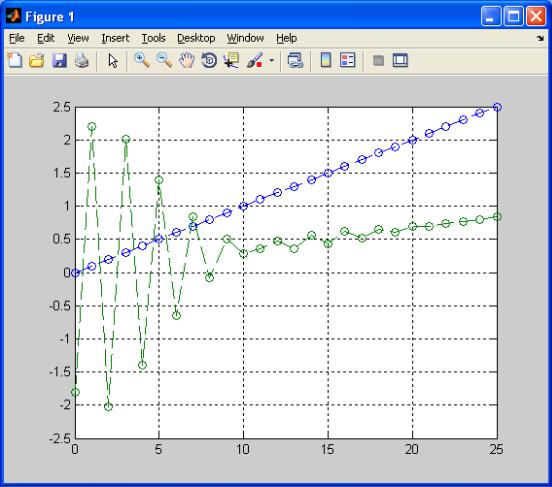
Чтобы проиллюстрировать колебательный характер решения разностного уравнения можно увеличить верхнее значение для переменной цикла (например, принять его равным 25). Графическое решение разностного уравнения при данном значении показано на рисунке 4.2.
Рисунок 4.2 Значения решения разностного уравнения yk и его правой части gk
4.2. Решение разностных уравнений методом z-преобразования
Задача 2. Найти методом z-преобразования решение разностного уравне-
ния |
|
|
2yk 3yk 1 1,12yk 2 2 1(k) |
(4.3) |
|
при нулевых начальных условиях ( y 1 0 и |
y 2 0 ) и построить его график. |
|
Решение. Перейдѐм в уравнении (4.3) к z-преобразованиям с учѐтом за- |
||
данных нулевых начальных условий. Если |
Z{yk } y(z) , |
то в соответствии с |
теоремой запаздывания имеем:
Z{yk 1} z 1 y(z) , Z{yk 2 } z 2 y(z) .

27
По таблице 4.1 z-изображений находим также Z{1[k]} z /(z 1) . Подставляя z-изображения вместо переменных в (4.3) и группируя подобные члены, по-
лучим |
|
|
|
|
|
|
|
(2 - 3z 1 1,12z 2 ) y(z) 2 |
z |
|
|||
|
|
. |
|
|||
|
z 1 |
|
||||
Отсюда следует |
|
|
|
|
|
|
y(z) |
2z |
|
|
|
z |
|
|
|
|||||
(z 1)(2 3z 1 1,12z 2 ) |
(z 1)(1 1,5z 1 0,56z 2 ) |
|||||
|
z3 |
|
|
. |
|
(z 1)(z 2 1,5z 0,56) |
||
Теперь для решения уравнения достаточно найти оригинал полученного выражения
y(z) |
z3 |
|
(z 1)(z 2 1,5z 0,56) . |
(4.4) |
Для этого вынесем за скобки z, а оставшуюся дробь разложим на простейшие
дроби. Корни уравнения |
z 2 1,5z 0,56 0 |
|
равны |
z 0,7 |
, |
z |
2 |
0,8 |
. Поэтому |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
правую часть выражения (5.4) можно представить в следующем виде: |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
z 2 |
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
B |
|
|
|
|
|
|
|
C |
|
|
|
|
|||||||
z |
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.5) |
|||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
(z 1)(z |
1,5z 0,56) |
|
|
|
|
(z 1) |
|
|
(z 0,7) |
|
z 0,8 |
. |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Неопределѐнные коэффициенты A, B и C в данном равенстве найдем, умно- |
|||||||||||||||||||||||||||||||||||||||||
жая обе части равенства на множители (z 1), (z 0,7) и (z 0,8) |
и полагая |
||||||||||||||||||||||||||||||||||||||||
соответственно z 1, z 0,7 и z 0,8 . В результате получим: |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
A |
|
|
|
z 2 |
|
|
|
|
|
|
|
|
z 1 |
|
|
1 |
|
16,67 , |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
(z 0,7)(z 0,8) |
|
|
0,3 0,2 |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
B |
|
|
|
|
|
|
z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,49 |
|
|
|
|
16,33 |
, |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
(z 1)(z 0,8) |
z 0,7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0,3 ( 0,1) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
C |
|
|
|
z2 |
|
|
|
|
|
z 0,8 |
|
|
0,64 |
|
|
|
|
32 . |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
(z |
1)(z 0,7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0,2 0,1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
Подставляя полученные значения в (4.5), а затем в (4.4), получим |
|||||||||||||||||||||||||||||||||||||||||
|
y(z) |
16,67 |
|
z |
|
|
|
16,33 |
|
|
z |
32 |
|
|
|
z |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
. |
|
|
|
|
||||||||||||||||||||||||||||||
|
z 1 |
z 0,7 |
z 0,8 |
|
|
|
|
||||||||||||||||||||||||||||||||||
Используя таблицу z-преобразований основных функций (таблица 4.1), |
|||||||||||||||||||||||||||||||||||||||||
можно записать следующие соответствия: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
z |
|
|
1[k], |
|
z |
|
|
0,7k |
, |
|
|
|
z |
0,8k . |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
z 0,7 |
|
|
|
0,8 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
z 1 |
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Таким образом, решение заданного уравнения имеет вид yk 16,67 1[k] 16,33 (0,7)k 32 (0,8)k .
28
Таблица 4.1 Изображения основных непрерывных и дискретных функций
№ |
|
|
|
f(t) |
F(s)=L{f(t)} |
|
|
|
f(kT) |
|
|
|
|
|
|
F(z)=Z{f(kT)} |
||||||||||||||||||||||||||||||||||
п/п |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
(t) |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
(kT) |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2. |
|
|
|
|
1(t) |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1(kT) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 1 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3. |
|
|
|
|
|
|
t |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
(kT) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T z |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(z 1)2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
s 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
4. |
|
|
|
|
|
t 2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
(kT)2 |
|
|
|
|
|
|
|
T 2 z(z 1) |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
s 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2!(z 1)3 |
|||||||||||||||||
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
5. |
|
|
|
|
|
|
t 3 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
(kT)3 |
|
|
|
|
|
|
|
T 3 z(z 1) |
|
||||||||||||||||||
|
|
|
|
|
|
3! |
|
|
|
|
|
|
s 4 |
|
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
|
|
|
3!(z 1)4 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
6. |
|
|
e |
t |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
e |
kT |
|
|
|
|
|
|
z |
|
|
|
, |
|
q e T |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z q |
||||||||||||||||||||||||||
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
7. |
|
1 e t |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 e kT |
|
|
|
|
(1 q)z |
|
|
|
, q e T |
|||||||||||||||||||||||||
|
|
(s ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(z 1)(z q) |
|||||||||||||||||||||||||||||||
8. |
|
|
te t |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
kTe kT |
|
|
|
|
|
|
zq |
|
|
|
|
|
|
, q e T |
||||||||||||||||||
|
|
|
|
(s ) |
2 |
|
|
|
|
|
|
|
|
|
(z q) |
2 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
9. |
|
|
t |
e t |
|
|
|
|
|
|
|
|
|
|
|
|
|
(kT) |
e kT |
|
|
|
z(z q)q |
, q e T |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
(s ) |
3 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
2!(z q) |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
10. |
|
|
sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
sin( βkT) |
|
|
|
|
|
|
|
|
|
z sin T |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
s 2 |
2 |
|
|
|
|
|
|
|
z 2 2z cos T 1 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
11. |
|
|
cos t |
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
cos( βkT) |
|
|
|
|
|
|
z 2 z cos T |
|||||||||||||||||||||||||
|
|
|
|
|
s 2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
z 2 2z cos T 1 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
12. |
e |
t |
|
|
sin t |
|
|
|
|
|
|
|
|
|
|
|
e |
kT |
sin( βkT) |
|
|
|
|
|
|
ze T sin T |
||||||||||||||||||||||||
|
|
|
|
|
|
(s )2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
z 2 2ze T cos T e 2 T |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
13. |
e |
t |
|
cos t |
|
|
|
|
s |
|
|
|
|
e |
kT |
cos(βkT) |
|
|
|
|
|
z(z e T cos T ) |
||||||||||||||||||||||||||||
|
|
|
|
(s )2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
z 2 2ze T cos T e 2 T |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
Для вычисления yk в системе MATLAB запишем следующую простую программу (скрипт) на M-языке:
%Задать начальные значения yk_2=0; yk_1=0;
%Создать вспомогательные массивы y1=[]; y2=[];
%Организовать цикл
kmax=25;
i=0:kmax; for k=i
y1=[y1; 16.67+16.33*0.7^k-32*0.8^k]; yk=(-1.12*yk_2+3*yk_1+2)/2;
|
|
|
29 |
y2=[y2;yk]; |
|
||
yk_2=yk_1; yk_1=yk; |
|
||
end |
|
|
|
disp(' |
k |
y1k |
y2k') |
disp([i' y1 |
y2]) |
|
|
plot(i', y1, 'o-'), grid on |
|
||
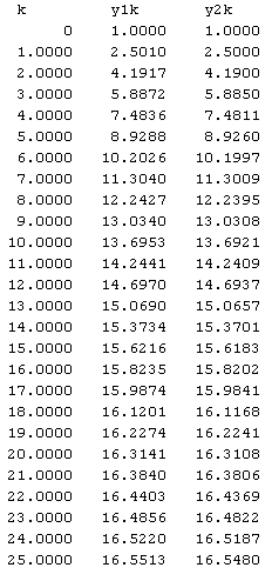
В результате выполнения данной программы в окне команд будет отображен следующий результат вычислений:
Здесь в столбце «y1k» помещены результаты вычисления решения разностного уравнения, а в столбце «y2k» показаны значения, вычисленные рекуррентным способом; как видно, соответствующие значения в обоих столбцах совпадают c точностью первого знака после десятичной точки (запятой). Если же десятичные значения коэффициентов A и B представить 50/3 и 49/3, то совпадение будет с точностью до четвертого знака после десятичной точки. График полученного решения показан на рисунке 4.3.

30
Рисунок 4.3 График решения разностного уравнения
4.3. Индивидуальные задания по лабораторной работе
Задание 1. Найти значения y0 y12 решения следующего разностного уравнения рекуррентным методом:
yk 0,8yk 1 0,012yk 2 0,01yk 3 0,5k ,
при y 1 0 , y 2 1, y 3 0,5 .
Задание 2. Найти значения y0 y12 решения следующего разностного уравнения рекуррентным методом:
yk 0,6yk 1 0,08yk 2 2 1[k] 0,2k ,
при y 1 0,5 , y 2 1.
Задание 3. Найти методом z-преобразования решения следующих разностных уравнений при нулевых начальных условиях и построить их графики (использовать MATLAB):
1)yk 0,6yk 1 0,08yk 2 0,5k ;
2)yk yk 1 0,34yk 2 1[k] 0,6k ;
3)3yk 1,8yk 1 0,28yk 2 4,5k .
