4360

11

Лабораторная работа №2. Работа с комплексными числами и вычисление корней полиномов в системе MATLAB (4 часа)

Цель работы: Знакомство с системой математического моделирования MATLAB на примере работы с комплексными числами и вычисления корней полиномов (решения квадратных уравнений).

Примечание. Аргумент комплексного числа определяется с точностью до слагаемого 2k , где k любое целое число. При этом положительные значения (z) отсчитываются против хода часовой стрелки, отрицательные по ходу часовой стрелки.

Задача 1. Найти модуль и фазу комплексного числа z 4 j 3. Показать это число, его модуль и фазовый угол на комплексной плоскости.

Решение. В данном случае Re z 4, Imz 3. Следовательно, модуль и

Решение в MATLAB:

%Вводим комплексное число

>> z=-4+j*3

%MATLAB выводит его в следующем виде z =

-4.0000 + 3.0000i

%Вычислим модуль комплексного числа

>> abs(z) ans =

5

12

%Вычислим фазовый угол в радианах

>> angle(z) ans =

2.4981

%Вычислим фазовый угол в градусах

>> angle(z)*180/pi ans =

143.1301

>>

Задача 2. Найти третью степень, натуральный и десятичный логарифмы комплексного числа z 2 j 3.

Решение. Для удобства определения степеней и логарифмов комплексного числа сначала представим заданное число z в показательной форме z z е j ( z) .

По формулам (1.1) и (1.2) рассчитаем модуль и фазу заданного числа: z 4 9 3,6056, (z) arctg 32 0,9828 рад 56,31 ,

т.е. z 3,6056 е j 0,9828.

Следовательно,

(2 j 3)3 3,60563 е j3 0,9828 46,872 e j 2,948446,872( 0,9814 j 0,192) 46 j 9.

Решение в MATLAB:

%Вводим комплексное число

>> z=2-3*j

%MATLAB выводит его в следующем виде z =

2.0000 - 3.0000i

%Вычислим третью степень комплексного числа z >> z3=z^3

z3 =

-46.0000 - 9.0000i

%Вычислим модуль третьей степени комплексного числа z >> abs(z3)

ans = 46.8722

%Вычислим фазу третьей степени комплексного числа z

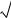
13

>> angle(z3)*180/pi ans =

-168.9298

%Вычислим натуральный логарифм комплексного числа z >> ln_z=log(z)

ln_z =

1.2825 - 0.9828i

%Вычислим модуль натурального логарифма комплексного числа z >> abs(ln_z)

ans = 1.6157

%Вычислим фазу натурального логарифма комплексного числа z в

%градусах

>> angle(ln_z)*180/pi ans =

-37.4639

%Выполним проверку в MATLAB >> exp(ln_z)

ans =

2.0000 - 3.0000i

%Вычислим десятичный логарифм комплексного числа z >> lg_z=log10(z)

lg_z =

0.5570 - 0.4268i

%Выполним проверку в MATLAB

>> 10^(lg_z) ans =

2.0000 - 3.0000i

2.2. Нахождение корней полиномов (многочленов)

Задача 3. Найти корни полинома 2x2 12x 16 и представить полином в виде произведения сомножителей.

Решение. Корни полинома это корни уравнения, которое получается путем приравнивания этого полинома к нулю. Следовательно, требуется найти корни уравнения 2x2 12x 16 0 . Для определения корней квадратного уравнения (полинома второй степени) используются две формулы.

где D b2 4ac дискриминант уравнения. Если D 0 , уравнение будет иметь вещественные корни; если D 0 , корни уравнения будут комплексными.

16

Лабораторная работа №3. Решение обыкновенных дифференциальных уравнений в системе MATLAB (4 часа)

Цель работы: Знакомство с системой математического моделирования MATLAB на примере решения обыкновенных дифференциальных уравнений.

3.1. Общие сведения

Поведение линейных, непрерывных, стационарных систем с сосредоточенными параметрами описывается во времени обыкновенным дифференциальным уравнением (ОДУ) с постоянными коэффициентами ai, bj

где слева – выходная функция y(t) и ее производные (результат), справа – входная функция x(t) и ее производные.

Данное уравнение можно записать в алгебраизованном виде, используя оператор (символ) дифференцирования p ≡ d/dt, что позволяет производить с дифференциальным уравнением алгебраические операции – выносить члены за скобки, складывать, умножать и т. п.

(a0 pn + a1 pn-1 + ... + an ) y(t) = (b0 pm + b1 pm-1 + ... + bm ) x(t).

Здесь слева в скобках – собственный оператор объекта управления, справа – оператор входа (воздействия). При этом в алгебраизированном уравнении используются, как правило, не сами величины x и y, а их абсолютные ∆y/∆x или относительные ∆y/y0, ∆x/x0 отклонения от рабочей точки c координатами (x0, y0).

Оператор D(p) = a0 pn + a1 pn-1 + ... + an называется также характеристическим, так как характеризует собственные свойства системы (объекта), а уравнение D(p) = a0 pn + a1 pn-1 + ... + an = 0 – характеристическим уравнением системы.

3.2.Решение обыкновенных дифференциальных уравнений в системе математического моделирования MATLAB

Задача 1. Найти решение однородного дифференциального уравнения

MATLAB. Написать программу (скрипт) для построения графика полученной функции в MATLAB.

Решение. Классический метод решения однородных дифференциальных уравнений предполагает использование соответствующих характеристических

17

уравнений. В данном случае характеристическое уравнение имеет следующий вид:

3k 2 18k 75 0 .

Корнями характеристического уравнения являются k1,2 3 4 j . По-

скольку корни комплексные, общее решение уравнения (3.1) имеет следующий вид:

Затем, полагая в выражениях для yобщ (t) и yобщ (t) переменную t 0 , приравня-

ем их к заданным начальным условиям. В результате получим систему двух алгебраических уравнений

однородного дифференциального уравнения (3.1), которое удовлетворяет заданным начальным условиям.

Решение в MATLAB. Для решения систем обыкновенных дифференциальных уравнений в системе MATLAB реализованы различные численные методы, называемые решателями (solvers). Помимо численных методов в MATLAB реализована возможность символьного решения обыкновенных дифференциальных уравнений. В частности, решение заданного дифференциального уравнения в символьном виде имеет следующий вид:

>> y=dsolve('3*D2y+18*Dy+75*y=0', 'y(0)=-5', 'Dy(0)=-3')

y = -(5*cos(4*t))/exp(3*t) - (9*sin(4*t))/(2*exp(3*t))

18

Рисунок 3.1 Программа для вывода графика функции y(t) e 3t ( 5cos 4t 4,5sin 4t)

После запуска программы на экране в специальном окне (рисунок 3.2) отображается график функции y(t) e 3t ( 5cos 4t 4,5sin 4t) .

Рисунок 3.2 График функции y(t) e 3t ( 5cos 4t 4,5sin 4t)

Задача 3.2. Найти решение неоднородного дифференциального уравне-

MATLAB. Написать программу для построения графика полученной функции в

MATLAB.

Решение. Решение неоднородного дифференциального уравнения всегда

равно сумме y(t) yобщ(t) yчаст (t) , где yобщ (t) общее решение соответствующего однородного дифференциального уравнения, которое в данном случае

Поскольку показатель экспоненты в первой составляющей внешнего воздействия 5e 3t совпадает с корнем k2 3 характеристического уравнения, то имеет место так называемый случай резонанса и, следовательно, yчаст1(t) Dte 3t . Вторая составляющая yчаст2 (t) A, поскольку в этом случае резонанса нет. Здесь A, D некоторые коэффициенты.

Для определения значений этих коэффициентов найдем yчаст (t) и yчаст (t) , а затем подставим yчаст (t) и эти производные в уравнение (3.6). В результате получим равенство Dte 3t 12A 5te 3t 2 . Приравняв выражения перед экс-

yчаст (t) 5te 3t 1/ 6 .

Таким образом, полное решение неоднородного дифференциального

решения однородного дифференциального уравнения, т.е. исходя из заданных начальных условий. В данном случае соответствующая система алгебраических уравнений имеет вид

Решение этой системы уравнений дает С1 7 / 2, C2 8/ 3 . Подставляя значения С1 и C2 в (3.8), получим искомое решение

Решение в MATLAB. Решение неоднородного дифференциального уравнения в символьном виде имеет следующий вид:

>> y=dsolve('D2y+7*Dy+12*y=5*exp(-3*t)+2', 'y(0)=1','Dy(0)=-1')

y = 7/(3*exp(3*t)) + 7/(2*exp(4*t)) + (5*t + (2*exp(3*t))/3)/ exp(3*t) - (exp(4*t)/2 + 5*exp(t))/exp(4*t)

>> y=simplify(y)

y = 7/(2*exp(4*t)) - 8/(3*exp(3*t)) + (5*t)/exp(3*t) + 1/6

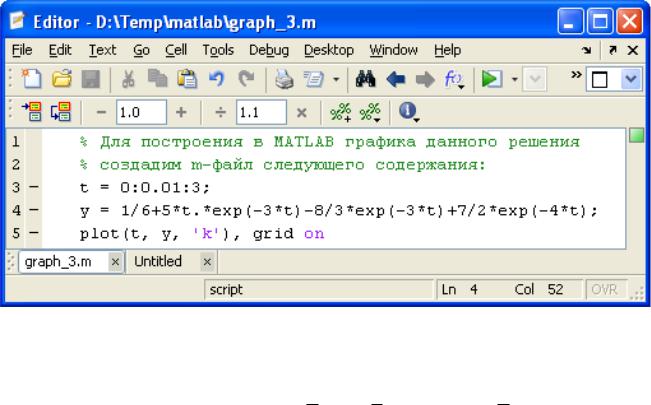
представленную на рисунке 3.3.

Рисунок 3.3 Программа для вывода графика функции

После запуска программы на экране в специальном окне (рисунок 3.4) отображается график функции y(t) 72 e 4t 83 e 3t 5te 3t 16 .