3716

Лекция 3 Статистические методы анализа данных и планирование эксперимента

3.1Понятие регрессии и корреляции

3.2Корреляционный анализ

3.3Регрессионный анализ

3.1Понятие регрессии и корреляции

Одна из наиболее распространенных задач статистического исследования состоит в изучении связи между выборками. Обычно связь между выборками носит не функциональный, а вероятностный (или стохастический) характер. В этом случае нет строгой, однозначной зависимости между величинами. При изучении стохастических зависимостей различают корреляцию и регрессию. Понятия регрессии и корреляции непосредственно связаны между собой, но при этом существует четкое различие между ними. В корреляционном анализе оценивается сила стохастической связи, в регрессионном анализе ее формы.

x - независимая переменная, объясняющая, входная, предсказывающая, экзогенная, фактор, регрессор, факторный признак;

y - зависимая переменная, функция отклика, объясняемая, выходная, результирующая, эндогенная переменная, результативный признак.

Таким образом, определяется зависимость случайной переменной Y от

независимой переменной X .

M x Y f x

3.2 Корреляционный анализ

Корреляционный анализ - метод, позволяющий обнаружить зависимость между несколькими случайными величинами.

Корреляция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой

21

степенью точности считать таковыми). При этом изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Мерой корреляции двух случайных величин служит коэффициент корреляцииR.

Корреляционной зависимостью между двумя переменными называется функциональная зависимость между значениями одной и средним значением

другой (условным математическим ожиданием),

M x Y f x

Это уравнение называется уравнением регрессии (или функцией регрессии, а её график – линией регрессии).

Для точного описания уравнения регрессии необходимо знать условный закон распределения переменной Y при условии, что переменная X примет значение x ,

Встатистической практике такой информации получить не удается, т.к. обычно имеется выборка пар значений xi , yi объема n .

Вэтом случае речь может идти о приближенном выражении, аппроксимации по выборке функции регрессии. Такой оценкой является выборочная линия (кривая) регрессии

^ y f x, a, b1, , bp

Поэтому регрессионная модель имеет вид:

Y f x

где Y - наблюдаемое значение зависимой переменной, f x - объясненная часть (подбираемая зависимость между Yи x), зависящая от значений объясняющих переменных, - случайная составляющая.

В многомерном случае, когда х – вектор, x j , где j 1, p - могут считаться как случайными, так и детерминированными.

22

Y f x1, , x p .

Чтобы получить достаточно достоверные и информативные данные о распределении какой-либо случайной величины, необходимо иметь выборку её

переменных x, y .

Различают линейные и нелинейные регрессии. Нелинейные регрессии делят на два класса: регрессии, нелинейные относительно включенных объясняющих переменных, но линейных по оцениваемым параметрам, и,

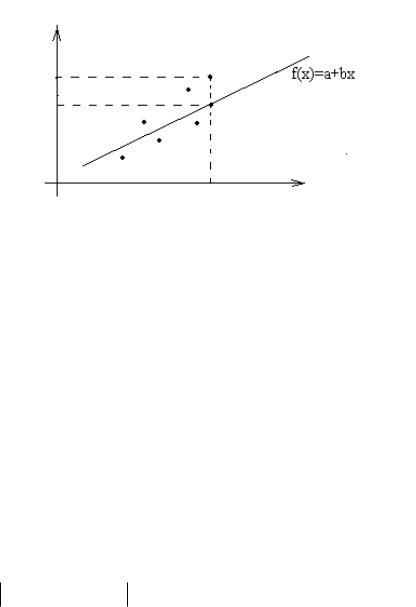
получаем поле корреляции, которое изображено на рис. 1.

23

xi

Рисунок 1 - Поле корреляции

Предположим, что нашей задачей является подобрать (подогнать) функцию из параметрического семейства функций f x, a, b , наилучшим способом описывающую зависимость y от x.

Подобрать функцию – это два шага:

1шаг: спецификация модели

2шаг: выбрать наилучшие значения параметров a и b .

При выполнении регрессионного анализа в качестве меры отклонения определяемой функции f x, a, b от набора наблюдений можно вычислять:

n

1. g yi f xi , a, b 2 - метод наименьших квадратов;

i 1

n

2. g yi f xi , a, b - метод наименьших модулей;

i 1

n

3. в общем случае: g F yi f xi , a, b ,

i 1

где F - мера, с которой отклонение yi f xi , a, b входит в функционал

g .

Таким образом, понятие корреляции дает возможность судить о том насколько тесно экспериментальные точки ложатся на прямую линию (линию регрессии). Если регрессия определяет предполагаемое соотношение между переменными, то корреляция показывает, насколько хорошо это соотношение отражает действительность. Количественно тесноту связи между переменными случайными величинами оценивают коэффициентом корреляции r.

24

Коэффициент корреляции — параметр, который характеризует степень линейной взаимосвязи между двумя выборками, для парной регрессии рассчитывается по формуле:

Рассмотрим взаимосвязь коэффициента корреляции и дисперсии для линейной многофакторной зависимости

y = b0+ b1x1+ b2x2+ ... + bnxn

полная изменчивость параметра y около среднего значения (дисперсия S2 ) складывается из двух частей:

1.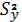,R2 обусловленной изменением переменных, входящих в линейное уравнение

2.Остатка 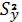=(1 – R2) который не зависит от переменных xi, а определяется действием неучтенных факторов.

Таким образом, коэффициент корреляции rхарактеризует долю полной изменчивости (полной дисперсии) параметра у, которая вызвана действием контролируемых переменных xi .

Чем больше r, тем теснее корреляционная связь, тем сильнее найденная зависимость проявляется среди многообразных, случайных воздействий, тем точнее по данным значениям xi можно предсказать значение у.

Свойства коэффициента корреляции:

1)1 r 1, т.к. cov x, y x y ;

2)при r 1 , корреляционная связь представляет линейную

функциональную зависимость. При этом все наблюдаемые значения располагаются на прямой (рис.2)

Рисунок 2 – Примеры корреляционная связь представляет

25

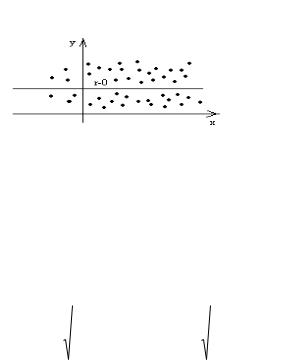
3) при r 0 линейная связь отсутствует (рис.), при этом близость к нулю не означает отсутствия связи между признаками, она может оказаться достаточно тесной.

Рисунок 3 - Отсутствие связи

В случае парной регрессии для практических расчетов наиболее удобная формула:

т.к. по этой формуле r находится непосредственно из данных наблюдений, и на значении r не скажутся округление данных, связанные с расчетом средних и отклонений от них.

3.3Регрессионный анализ

Спомощью уравнения регрессии y=ƒ(x1,x2,…xħ), , можно измерить влияние отдельных факторов на зависимую переменную, что делает анализ конкретным, существенно повышает его познавательную ценность, уравнения регрессии также применяются в прогнозных работах.

Построение уравнения регрессии предполагает решение двух основных задач. Первая задача заключается в выборе независимых переменных, оказывающих существенное влияние на зависимую величину, а также в определении вида уравнения регрессии.

Вторая задача построения уравнения регрессии – оценивание параметров (коэффициентов) уравнения. В связи с тем, что оценки параметров уравнения являются выборочными характеристиками, в процессе оценивания необходимо проводить статистическую проверку существенности полученных параметров.

Метод наименьших квадратов

26

При оценке параметров уравнения регрессии применяется метод наименьших квадратов (МНК). Смотрим применение МНК на примере однофакторной линейной регрессии y a bx .

Согласно МНК поиск наилучшей аппроксимации набора наблюдений линейной функцией сводится к минимизации функционала

выборочной ковариации cov x, y yx y x .

В новых обозначениях система определения a и b принимает вид:

Тогда

27

уравнение прямой y a bx проходит через точку x, y .

При выполнении линейного регрессионного анализа делаются определенные предпосылки относительно случайной составляющей

y a b1 x1 b p x p ,

где - ненаблюдаемая величина (остаток регрессии).

После того, как произведена оценка параметров модели, рассчитывая разности фактических и теоретических значений y , можно определить оценки случайной составляющей y yтеор . Поскольку они не являются реальными случайными остатками, их можно считать некоторой выборочной реализацией неизвестного остатка заданного уравнения, т.е. i . При изменении спецификации модели, добавлении в неё новых наблюдений, выборочные оценки остатков i могут меняться. Поэтому в задачу регрессионного анализа входит не только построение самой модели, но и исследование случайных отклонений i , т.е. остатков.

До сих пор мы останавливались на формальных проверках статистической достоверности коэффициентов регрессии и корреляции с помощью t - критерия Стьюдента, F - критерия Фишера. Оценки параметров регрессии должны отвечать определенным критериям. Они должны быть несмещенными, состоятельными и эффективными.

Несмещенность оценки означает, что математическое ожидание остатков равно нулю. Следовательно, при большом числе выборочных оценивании, остатки не будут накапливаться и найденный параметр b можно рассматривать как среднее значение из возможного большого числа несмещенных оценок.

Эффективность оценки – оценки, характеризующиеся наименьшей дисперсией.

Состоятельность оценок характеризует увеличение их точности с увеличением выборки.

28

Указанные критерии должны учитываться при разных способах оценивания. МНК строит оценки регрессии на основе минимизации суммы квадратов остатков. Поэтому очень важно исследовать поведение остатков регрессии i .

Исследования остатков i предполагают проверку наличия следующих предпосылок МНК (т.е. предполагается получение несмещенных эффективных

исостоятельных оценок):

1.случайный характер остатков

2.нулевая средняя величина i , не зависящая от xi

3.гомоскедастичность – дисперсия каждого i одинакова для всех

значений x

4.отсутствие автокорреляции остатков. Значения остатков i

распределены независимо друг от друга.

5. остатки подчиняются нормальному распределению. Оценка значимости уравнения регрессии

Проверить значимость уравнения регрессии - значит установить,

соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.

Проверка значимости уравнения регрессии производится на основе дисперсионного анализа.

^

Обозначим через y a bx - теоретически вычисляемые по формуле значения, тогда

Введем обозначения:

TSS (totalsumofsguares) – вся дисперсия: сумма квадратов отклонений от среднего.

RSS (regressionsumofsguares) – объясненная часть всей дисперсии (обусловленная регрессией), факторная, объясненная дисперсия.

ESS (errorsumofsguares) – остаточная сумма, дисперсия остаточная.

29

Коэффициентом детерминации R2 , или долей объясненной дисперсии называется

^

yi yi .

Соответственно коэффициент линейной регрессии (как парной так и множественной)

Использование F-критерия

С помощью F-критерия можно оценить качество построенной функции y a bx .

Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений, или, что тоже самое, дисперсию на одну степень свободы D

Это приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточные дисперсии в расчете на одну степень свободы, получим величину F - отношения (F- критерия):

Dфакт

F Dостат ,

где F- критерий для проверки нулевой гипотезы H 0 : Dфакт Dост .

30