3716

функции следует учитывать, а какие не вписываются в рамки поставленной задачи. В планировании эксперимента любого исследователя, прежде всего интересует как поведёт себя система, если на неё подействовать определённым образом. При этом ни одного из экспериментаторов абсолютно не интересует, что при этом «чувствует» сама система. Модели подобного рода, когда рассматривается только влияние на объект и его ответ на это влияние без учета внутренних процессов объекта, часто представляются так называемым черным ящиком.

Как же найти те оптимальные условия эксперимента, которые нас интересуют? Причём было бы неплохо, если бы этот поиск не требовал особых затрат. В этом случае мы прибегаем к математической модели эксперимента, с помощью которой можно предсказывать отклик системы в тех состояниях, которые экспериментально не изучались. В этом случае появляется возможность прогнозирования результатов эксперимента в точках, являющихся оптимальными в рамках поставленной задачи. И здесь мы переходим к пошаговому принципу.

Однако, прежде, чем приступить к моделированию, необходимо определиться с основными требованиями к поверхности отклика, на основе которой мы и собираемся делать прогнозы.

Требование № 1.

Непрерывность поверхности - если в какой-либо точке факторного пространства функция отклика терпит разрыв, нет никакой гарантии, что при реальном осуществлении эксперимента данное состояние, либо вообще невозможно, либо привлечёт к фатальным последствиям. При выборе большого шага перебора уровней факторов можно просто не заметить этот разрыв, «перешагнув» через него, однако вероятность попадания в эту критическую область на практике довольно-таки велика, и результат будет самым непредсказуемым.

Требование № 2.

Гладкость поверхности отклика (соображения те же, что и в предыдущем пункте).

Требование № 3.

Наличие единственного оптимума. Данное требование, пожалуй, одно из самых важных. При планировании эксперимента поиск оптимума может вестись в разных направлениях - и вправо, и влево. Если оптимумов несколько, да они и неравномерны, нет никакой гарантии, что наткнувшись на один из них,

11

мы посчитаем данный оптимум именно тем решением, который мы ищем, в то время, как это предположение неверно. Если же оптимум будет единственным, неважно с какой стороны мы будем к нему приближаться.

1.6. Принятие решения перед планированием

Подытоживая все выше сказанное, отмечу, что прежде чем заниматься планированием эксперимента, необходимо определиться с некоторыми вопросами.

1.Во-первых, следует точно определиться с понятием объекта исследования, дав ему точное формальное определение.

2.Во-вторых, прежде чем приступить к эксперименту, необходимо однозначно и непротиворечиво сформулировать цель эксперимента, определиться с параметрами оптимизации. Параметр оптимизации должен быть единственным, хотя он и может принимать различные значения.

3.В-третьих, необходимо определиться с факторами, влияющими на ход эксперимента и с тем, какие значения принимают эти факторы. Влияющих факторов, вообще говоря, может быть сколько угодно, при этом каждый из них может принимать бесконечное число значений. Однако не следует забывать, что в зависимости от числа факторов и их уровней катастрофически растёт и число экспериментов. Выбирая, скажем, порядка двадцати факторов, каждый из которых имеет, например, по два уровня, мы можем обречь себя на долгие годы «мучений».

4.В-четвёртых, необходимо озадачить с поиском области проведения эксперимента. И здесь должны учитываться следующие соображения.

а) прежде всего, необходимо оценить границы областей определения факторов. При выборе границ учитываются ограничения нескольких типов: принципиальные ограничения; технико-экономические ограничения; конкретные условия проведения процесса (наиболее часто встречающийся тип ограничений).

Таким образом, выбор экспериментальной области факторного пространства связан с тщательным анализом априорной информации.

12

б) на втором этапе необходимо найти локальную область для планирования эксперимента. Данная процедура включает в себя два этапа: выбор основного условия; выбор интервалов варьирования.

Интервалом варьирования факторов называется некоторое число (свое для каждого фактора), прибавление которого к основному уровню дает верхний уровень, а вычитание - нижний уровень.

5. И, наконец, необходимо помнить, что для грамотного исследователя является главной целью не поиск материальных благ, приобретаемых при оптимизации процесса, а построение математической модели объекта исследования, представляющей собой математическое уравнение, связывающее параметр оптимизации и факторы, т.е. функции отклика. Наличие функции отклика «под рукой» поможет в дальнейшем решать новые задачи с наименьшими затратами по исследованию объекта.

Вопросы

1.Дайте определение понятию «Планирование эксперимента».

2.Задача «Планирования эксперимента»?

3 Дайте определение понятию «Промышленный эксперимент»

4Дайте определение понятию «Научно-исследовательский эксперимент»

5Дайте определение понятию «Лабораторный эксперимент»

6Дайте определение понятию «Оптимальный (экстремальный) эксперимент»

7Дайте определение понятию «Пассивный эксперимент»

8Дайте определение понятию «Пошаговый эксперимент»

9Дайте определение понятию «Активный эксперимент»

10Дайте определение величине - параметр оптимизации (отклик).

11Дайте понятие величине «фактор».

12Что называется интервалом варьирования факторов?

13

ЛЕКЦИЯ 2.

Статистическая проверка статистических гипотез.

2.1.Статистические гипотезы.

2.2.Виды ошибок при выдвижении статистических гипотез.

2.3.Методы проверки гипотез

2.1.Статистические гипотезы

Гипотеза – это научно обоснованное высказывание вероятностного характера о сущности изучаемых явлений действительности. Гипотеза - это всегда утверждение.

Если гипотеза подтвердилась, то ее принимают, если не подтвердилась, то отвергают. Принятая гипотеза может в последующем при соответствующих дополнительных доказательствах ее жизнеспособности и плодотворности преобразоваться в теорию. Выдвинутая до эмпирического исследования гипотеза обычно называется исследовательской или рабочей. Рабочая гипотеза дает первый, предварительный проект решения проблемы.

Взависимости от логического пути развития гипотезы различают: гипотезы индуктивные и дедуктивные. Первые рождаются из наблюдения за отдельными фактами, вторые – выводятся из уже известных отношений или теорий.

Вматематической статистике различают нулевую и альтернативную (т.е.

исследовательскую) гипотезы.

Нулевая гипотеза (нуль гипотеза)— гипотеза, подлежащая проверке, гипотеза, которая проверяется на согласованность с имеющимися выборочными (эмпирическими) данными.

Альтернативная гипотеза – каждая допустимая гипотеза, отличная от нулевой.

Нулевую гипотезу обозначают Н0, альтернативную – Н1.

Вформализованном виде данные гипотезы примут следующий вид:

Н0 : μ = μ0 Н1 : μ ≠ μ0

где μ – неизвестное среднее значение генеральной совокупности (которое нас интересует); μ0 – заданное значение, в отношении которого проверяют

14

гипотезу; Х – среднее значение выборки (случайная величина), которое представляет μ.

Нулевая и исследовательская гипотезы взаимно исключают друг друга. Доказывать необходимо именно исследовательскую гипотезу, при этом, если доказательств окажется недостаточно, то принимается нулевая гипотеза. В процессе принятияотвержения гипотез возможны ошибки двух родов.

2.2 Виды ошибок при выдвижении статистических гипотез

Ошибка первого рода состоит в том, нулевая гипотеза отвергается, то есть принимается гипотеза Н1 , в то время как в действительности верна гипотеза Н0

.Т.е. ошибка первого рода: мы отклоняем гипотезу, когда она выполняется. Ошибка второго рода состоит в том, что принимается гипотеза Н0 , а в

действительности верна гипотеза Н1. Т.е. ошибка второго рода: мы принимаем гипотезу, когда она не выполняется.

Для любой заданной критической области будем обозначать через

вероятность ошибки первого рода, а через - вероятность ошибки второго рода. Следовательно, можно сказать, что при большом количестве выборок доля ложных заключений равна , если верна гипотеза Н0 , и , если верна гипотеза Н1. При фиксированном объёме выборки выбор критической области W позволяет сделать как угодно малой либо , либо .

Часто в качестве нулевой гипотезы Н0 выступают гипотезы об отсутствии взаимосвязи или корреляции между исследуемыми переменными, об отсутствии различий (однородности) в распределениях (параметрах распределений) двух и/или более выборках. Поэтому статистическая гипотеза – любое предположение, касающееся неизвестного распределения случайных величин (элементов).

Примеры формулировки нескольких статистических гипотез:

1.Результаты наблюдений имеют нормальное распределение с нулевым математическим ожиданием.

2.Результаты наблюдений имеют функцию распределения N(0,1).

3.Результаты наблюдений имеют нормальное распределение.

4.Результаты наблюдений в двух независимых выборках имеют одно

ито же нормальное распределение.

5.Результаты наблюдений в двух независимых выборках имеют одно

ито же распределение.

15

В стандартном научном подходе проверки гипотез исследователь пытается показать несостоятельность нулевой гипотезы, несогласованность её с имеющимися опытными данными, то есть отвергнуть гипотезу. При этом подразумевается, что должна быть принята другая, альтернативная (конкурирующая), исключающая нулевую, гипотеза.

Этапы проверки гипотезы Н0.

1.Формулируется проверяемая гипотеза Н0

2.Выбирается критерий проверки X. Критерий – это величина, закон распределения которой при условии справедливости проверяемой гипотезы известен.

3. Выбирается уровень значимости и критическая область Q, так, чтобы условная вероятность попадания критерия в Q при условии справедливости гипотезы равнялась .

4.Выполняем эксперимент и находим экспериментальное значение критерия Х.

5.Если критерий X не попадает в критическую область Q, гипотеза принимается, если X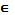Q – то отвергается.

Выбор критической области должен производиться с учетом смысла гипотезы; следует учитывать, что если Х попадает в критическую область, то гипотеза будет отвергнута

2.3Методы проверки гипотез

Существует два различных метода проверки гипотез. Первый – метод доверительных интервалов. Второй метод носит название t-тест, который более распространен на практике, и основан на расчете t-статистики.

Проверка гипотезы заключается в сравнении двух известных величин Х и

μ0,

где μ – неизвестное среднее значение генеральной совокупности (которое нас интересует);

μ0 – заданное значение, в отношении которого проверяют гипотезу; Х – среднее значение выборки (случайная величина), которое

представляет μ.

Если эти значения Х и μ0 «достаточно близки» между собой (Х = μ0), то принимается нулевая гипотеза. Если значения «сильно отличаются» друг от

16

друга (Х ≠ μ0), то принимается альтернативная гипотеза. «Близость» значений определяется на основе значения стандартной ошибкой Sx.

Метод «доверительных интервалов» заключается в построении диапазона значений на 95% уровне достоверности (см. таблицу ниже):

Если значениеμ0 находится за пределами доверительного интервала, то оно не может рассматриваться как возможное значение, т.е. равенство μ = μ0 не выполняется. Соответственно, выполняется условие μ ≠ μ0 , т.е. доказывается альтернативная гипотеза. В таком случае делается вывод о том, что нулевая гипотеза отклоняется и принимается альтернативная гипотеза на уровне достоверности 95%.

Метод «t – тест» заключается в расчете критерия Стьдента или t –

статистики, сравнении ее с табличным значением и формулировкой вывода. Коэффициент Стьюдента или t-статистику предложил В.С. Госсет (см.

таблицу ниже):

17

Для сравнения с табличным значением используется абсолютное значение t, т.е. «по модулю».

Критерий Стьюдента или t - статистика показывает на сколько стандартных ошибок отличаются между собой средние значения по выборке (Х) и генеральной совокупности (μ). Поскольку при 95% уровне достоверности значение t =1,96, то существует эмпирическое правило, что «приt>2 нулевая гипотеза отклоняется».

Считается, что результат проверки является статистически значимым, если альтернативная гипотеза принимается на уровне 5%. Для описания полученных результатов обычно пользуются следующими терминами:

значимый

При расчетах в Excel программа выводит р-значение, которое показывает вероятность того, что данные соответствуют нулевой гипотезе. Обычно Н0 отклоняют, если р < 0,05. Другими словами, вероятность того, что нулевая гипотеза истинна, не превышает 5% (что является статистически значимым).

Сравнение двух независимых выборок с применением t- критерия

Для двух несвязанных выборок(наблюдения не относятся к одной и той же группе объектов ) возможны два варианта расчета:

когда дисперсии известны

когда дисперсии неизвестны, но равны друг другу.

1.Предварительно проверяется нормальность закона распределения по одному из критериев согласия.

2.Рассчитывается средне арифметические значения X иY для каждой выборки по формуле

X1 n xi

n i 1

где xi – значение i-го результата наблюдения.

3.Рассчитывается tэмп - эмпирическое значение критерия Стьюдента:

18

В обоих случаев подсчет числа степеней свободы осуществляется по формулам

df (n1 1) (n2 1) n1 n2 2

При численном равенстве выборок 2n 2

4.Эмпирическое значение t'эмп критерия Стьюдента сравнивается с

критическим значением t'кр (по таблице 1 приложения) для данного числа степеней свободы.

Нулевая гипотеза H0 при заданном уровне значимости принимается,

если эмпирическое значение t'эмп. tкр .

Сравнение двух зависимых выборок с применением t- критерия

Под связанными выборками понимаются наблюдения для одной группы объектов, причем все наблюдения попарно связаны с каждый объектом исследования и характеризуют его состояние до воздействия и после воздействия некоторого фактора.

Гипотезы

H 0 : среднее значение в выборке не отличается от нуля.

H1 : среднее значение в выборке отличается от нуля.

Данные в выборке измерены по шкале интервалов или по шкале отношений. Сравниваемых выборок две для оной группы объектов наблюдения, причем имеет место парность наблюдений в выборках.

19

1.Предварительно проверяется нормальность закона распределения по одному из критериев согласия.

2.Рассчитывается i xi yi (i=1..n) – попарные разности вариант, xi и

yi результаты измерений для i-го объекта до и после воздействия некоторого фактора. Величину i будем считать независимой для разных объектов и нормально распределенной

3.Рассчитываются (лучше в табличной форме): сумма попарных

4.Рассчитывается týěď - эмпирическое значение критерия (n 1)

степенями свободы по формуле

данного числа степеней свободы.

Нулевая гипотеза H 0 при заданном уровне значимости принимается, если эмпирическое значение t'ýěď . tęđ .

Вопросы

1Дайте определение понятию «Гипотеза»

2Какие гипотезы различают в математической статистике?

3Какие существует два различных метода проверки гипотез?

4В чем заключается метод «доверительных интервалов»?

5В чем заключается Метод «t – тест»?

6Виды ошибок при выдвижении статистических гипотез

7Методы проверки гипотез?

20