Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежская государственная лесотехническая академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3533

.pdf

Скачиваний:

Добавлен:

08.01.2021

Размер:

582.47 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ЛЕСОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени Г.Ф. МОРОЗОВА»

Кафедра математики

Математический анализ

Методические указания к расчетно-графическим работам для студентов по направлению подготовки

38.03.01 – Экономика

Воронеж 2018

УДК 512.8

Раецкая, Е. В. Математический анализ [Электронный ресурс] : методические указания к расчетно-графическим работам для студентов по направлению подготовки 38.03.01 – Экономика / Е. В. Раецкая, П.Н. Зюкин, И.В. Сапронов; М-во образования и науки РФ, ФГБОУ ВО «ВГЛТУ». – Воронеж, 2018. – 16 с.

Одобрено решением учебно-методического совета

ФГБОУ ВО «ВГЛТУ»

(протокол № 6

от 23.03.2018 г.)

Рецензент: д-р физ.-мат. наук, проф. кафедры

математического анализа ВГУ С.П. Зубова

Содержание

Введение……………………………………………………………………………..4

1.1Полное исследование и построение графиков функций…………………5

1.2Варианты индивидуальных заданий по теме «Полное исследование и построение графиков функций»………………………………………………...9

2.1Вычисление неопределенных интегралов.………….…..…………………10

2.2Варианты индивидуальных заданий по теме «Вычисление неопределенных интегралов»…………………………………………………...12

Библиографический список…………………………………………………….16

ВВЕДЕНИЕ

Для эффективного освоения дисциплины «Математический анализ» у обучающегося должны быть сформированы представления об основных понятиях, идеях и методах математического анализа, а именно:

- представления о математике как части мировой культуры и о месте математики в современной цивилизации, о способах описания на математическом языке явлений реального мира;

- представления о математических понятиях как о важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий; В результате освоения дисциплины студент должен владеть:

-методами доказательств и алгоритмов решения; умение их применять, проводить доказательные рассуждения в ходе решения задач;

-стандартными приѐмами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств.

Студент по результатам освоения дисциплины «Математический анализ» должен обладать способностью выбрать инструментальные средства для обработки данных в соответствии с поставленной задачей, проанализировать результаты расчетов и обосновать полученные выводы.

1.1 ПОЛНОЕ ИССЛЕДОВАНИЕ И ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ

П р и м е р 1.			Исследовать методами дифференциального исчисления
функцию y	5x2		и на основании полученных результатов построить еѐ
	x2	25
график.
Решение.		Проведем исследование функции y		5x2	по следующей
				x2 25

схеме:

1. Область определения функции.

В область определения исследуемой функции не входят лишь те значения

x , для	которых x2 25 0 , то		есть		x 5	и x 5.	Поэтому
D( y) ( ; 5) ( 5;5) (5; ) .
2. Вид функции.
Выясним, является ли функция четной или нечетной.
Если	y( x) y(x)	для любого	x	из	области	определения	функции
y f (x) ,	то эта функция называется четной. График четной						функции
симметричен относительно оси ординат.
Если	y( x) y(x)	для любого	x	из	области	определения	функции

y f (x) , то эта функция называется нечетной. График нечетной функции

симметричен относительно начала координат. Для нашей функции:

y(x)	5x2		y( x)	5( x)2	5x2		y(x)	5x2
		,				,			.
	x2 25			( x)2 25	x2 25			x2 25

Видим, что y( x) y(x) для любого x из области определения функции.

Поэтому функция четная, еѐ график симметричен относительно оси ординат.

3. Точки пересечения графика функции с осями координат.

Для нахождения точек пересечения графика с осью Ox решим систему уравнений

		y 0,
				5x2
				5x2
	y					.
	y		x	2	25	.
			x		25
Отсюда получаем, что x 0 ,	y 0.			Следовательно, точка (0;0) является

точкой пересечения графика функции с осью Ox .

Для нахождения точки пересечения графика функции с осью Oy решим систему уравнений

	x 0,
			5x2
			5x2
y					.
y		x	2	25	.
		x		25

Отсюда x 0 , y 0, поэтому точка (0;0) является точкой пересечения графика функции с осью Oy .

4. Исследование функции по первой производной (интервалы монотонности, точки экстремума).

Найдем первую производную функции:

(5x2 ) (x2 25) 5x2 (x2

25)

10x (x2 25) 5x2 2x

25)

10x (x2

25 x2 )

250x

(x2 25)2

y 0

при

x 0 ,

не существует при x 5

x 5.

Точки

x1 5 ,

x2 0 ,

x3 5 разбивают область определения функции на четыре интервала

( ; 5) , ( 5;0) , (0;5) ,

(5; ) . Определим знак производной y

на каждом из

них. Возьмем

любое

число из интервала ( ; 5) ,

например

6 .

Так как

y ( 6)

250 ( 6)

1500

12,4 0 ,

поэтому

на всем

интервале

( ; 5)

(36 25)2

121

производная

y 0

и,

следовательно, функция монотонно возрастает.

Аналогично определяем знак производной y на трех других интервалах:

y ( 1)

250 ( 1)

250

0,4 0 ,

(1 25)2

576

y (2)

250 2

500

1,1 0

(4 25)2

441

y (7)

250 7

1750

3,1 0 .

(49 25)2

576

Результаты исследования занесем в таблицу:

( ; 5)

( 5;0)

(0;5)

(5; )

−

функция

возрастае

max

убыва

ет

Итак, функция возрастает на каждом из интервалов ( ; 5) ,

( 5;0) и

убывает на интервалах (0;5) , (5; ) . В точке

x 0 производная меняет знак с

«+» на «−», следовательно,

x 0

−

точка

максимума

функции. Значение

функции в этой точке равно:

ymax(0) 0 .

5. Исследование функции по второй производной (выпуклость,

вогнутость, точки перегиба графика). Найдем вторую производную функции:

	250x					(x) (x2 25)2		x ((x2 25)2 )

y ( y )					250
		2					2		4
	(x		25)	2		(x		25)

250		1 (x2 25)2 2x (x2 25) 2x							250			(x2 25) (x2 25 4x2 )
250				(x2 25)4					250			(x2	25)4
				(x2 25)4								(x2	25)4
250	3x		2 25	.
250	(x2		25)3	.
	(x2		25)3
y 0 , если 3x2				25 0 . Это уравнение не имеет решения.
y не существует при x 5							и x 5.
Точки x1 5 ,				x2 5	разбивают область определения функции на три
интервала: ( ; 5) , ( 5;5) ,					(5; ) . Определим знак производной y на каждом
из них. Так как			y ( 6) 250			3 62	25	250		133	274,8 0		, поэтому на всем

						(62 25)2				121
						(62 25)2				121
интервале ( ; 5) производная							y 0		и, следовательно,				график функции

является вогнутым на данном интервале. Аналогично определяем, что y 0 на интервале ( 5;5) , поэтому график выпуклый на данном интервале. На

интервале (5; )			y 0 ,	поэтому график	вогнутый на этом интервале.
Результаты исследования занесем в таблицу:

	x		( ; 5	( 5;5)	(5; )
	x			( 5;5)	(5; )

	y		+	−	+

	y
		вогнутый		выпуклый	вогнутый
	y		граф	выпуклый	вогнутый
	y		граф	график	график
			ик	график	график
			ик

Точек перегиба на графике функции нет.

6. Точки разрыва функции и вертикальные асимптоты её графика.

Точки разрыва функции – это точки x1 5								и x2 5 , в которых функция
не определена. Вычислим пределы функции в этих точках:
	5x2		125		5x2		125
lim				, lim				.
	2	25			2	25
x 5 x				x 5 x
			0				0

Поэтому прямые с уравнениями x 5 и x 5 являются вертикальными асимптотами графика функции.

7. Невертикальные асимптоты графика функции.

Невертикальной асимптотой будем называть асимптоту, не параллельную

оси Оу. Невертикальная асимптота графика функции

y f (x)

при

существует тогда и только тогда, когда существуют конечные пределы

lim

f (x)

lim[ f (x) kx] b .

Эта асимптота имеет уравнение y kx b .

Вычислим пределы

f (x)

lim

0 k ,

lim

x x (x2

25)

x x2

x 1

252

5x2

lim[ f (x) kx] lim

0 x

lim

5 b .

x x

x 1

Так

как

оба предела

k и

конечны,

то

график

функции

имеет

невертикальную асимптоту при x . Еѐ уравнение y kx b , то есть y 5 .

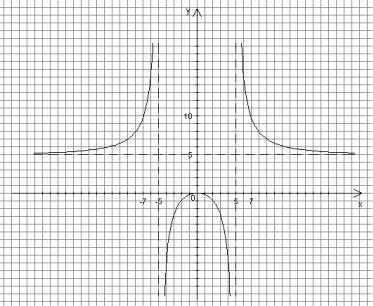
8. Построение графика функции.

На основании результатов проведенного исследования строим график функции.

Рис. 1 Четность функции облегчает построение графика: строим часть графика

функции для значений x [0;5) (5; ) , а затем отображаем эту часть графика

симметрично относительно оси ординат и получаем весь график.

Для уточнения графика рассмотрим несколько дополнительных точек:

	5 22		20				5 72	245
y(2)				0,9	,	y(7)			10,2 .
	22	25	21				72 25	24

9. Множество значений функции.

Вид графика (см. рис. 1) позволяет сделать вывод, что

E( y) ( ;0] (5; ) .

1.2 ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО ТЕМЕ «ПОЛНОЕ ИССЛЕДОВАНИЕ ФУНКЦИИ»

		Исследовать методами															дифференциального												исчисления функцию
y f (x) и на основании полученных результатов построить еѐ график.
1.	y						1									.	14.	y		1 x3								.
1.	y			x2			4x 3									.	14.	y					x2					.
				x2			4x 3																x2
2.	y					x3						.					15.	y			x2				2x							.
2.	y	6			2x2							.					15.	y					x			1						.
		6			2x2																		x			1
3.	y			x2		x 4									.		16.	y			x 2					.
3.	y					2x									.		16.	y					x3			.
						2x																	x3
4.	y					1						.					17.	y		x3					4			.
4.	y			x	2		2x					.					17.	y				3x2						.
				x	2		2x															3x2
5.	y				x2			.									18.	y					x3				.
5.	y			x2		1		.									18.	y		x2					1		.
6.	y				5x2						.						19.		y										1				.
6.	y		x2			25					.						19.		y						x2	4x 3							.
7.	y	1 x3							.								20.		y						x2 2x
7.	y				x2				.								20.		y						x 1
					x2																				x 1
8.	y					x3						.					21.	y			x2				2x							.
8.	y	6			2x2							.					21.	y					x			1						.
		6			2x2																		x			1
9.	y			x2		x 4									.		22.	y				x 2						.
9.	y					2x									.		22.	y						x3				.
						2x																		x3
10. y						1								.			23.	y			x3				4				.
10. y					x2									.			23.	y					3x2						.
					x2				2x														3x2
11. y						x2				.							24. y								x3					.
11. y					x2 1					.							24. y						x2 1							.
12. y						5x2							.				25.	y					5x2								.
12. y					x2 25								.				25.	y			x2				25						.
13. y					x2 x 4											.
13. y							2x									.
							2x

2.1 ВЫЧИСЛЕНИЕ НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ.

Пример 1.

Вычислить интеграл

x5 x x 2

dx .

Преобразуем подынтегральную функцию:

x5 x

x 2

x4 x

dx =

Тогда

x4dx

2 dx 2

2 ln

C .

x 3

Пример 2.

Вычислить интеграл

5 x2 dx .

Делаем замену

5 x2

t ,

тогда

2xdx dt

xdx

. Следовательно,

5 x2

4 C .

x 3

5 x2 dx =

xdx

3 C =

2 dt

Пример 3.

Вычислить интеграл

arctg2 x

dx .

1 x2

Делаем замену

arctgx t , тогда

dt .

1 x2

Следовательно,

arctg 2 x

dx = t

arctg3 x

2dt

C .

1 x2

Пример 4.

Вычислить интеграл

xsin 5x dx .

Воспользуемся формулой интегрирования по частям:

udv uv vdu .

x sin(5x)dx

u x

dv sin(5x)dx

x cos(5x)

cos(5x)

cos(5x)dx

x cos(5x)

sin(5x) C .

Пример 5.

Вычислить интеграл ln

2x dx .

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.01.2021580.72 Кб13529.pdf
#
08.01.2021190.34 Кб0353.pdf
#
08.01.2021580.74 Кб13530.pdf
#
08.01.2021581.57 Кб23531.pdf
#
08.01.2021582.32 Кб13532.pdf
#
08.01.2021582.47 Кб23533.pdf
#
08.01.2021582.49 Кб23534.pdf
#
08.01.2021582.64 Кб23535.pdf
#
08.01.2021582.83 Кб23536.pdf
#
08.01.2021583.18 Кб43537.pdf
#
08.01.2021583.34 Кб13538.pdf