
2622
.pdf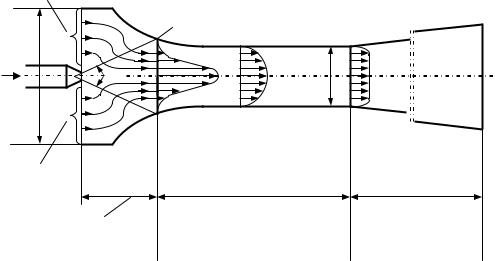
|
Воздух |
|
|
~2,2dГ |
Место отсечки |
|
|
dГ |
|
||
Газ |
а |
|
|
|
|
||
|
Воздух (2-3)dГ |
~ 5dГ |
LД |
|
Всасывающая |
Стабилизирующая |
Диффузор |
|
часть |
часть |
|
|
|
||
Рис. 60. Аэродинамическая картина работы эжектора с малой скоростью эжекции
Встабилизирующей части камеры смешения в результате турбулентной диффузии происходит выравнивание полей скоростей и концентраций, но соотношение между газом и воздухом уже не изменяется.
Статическое давление в пределах всасывающего участка практически остается постоянным, а в стабилизирующей части растет. Стабилизирующую часть камеры смешения вначале делают плавно сужающейся и в дальнейшем цилиндрической. Это обеспечивает стабилизацию с минимальными потерями.
Вместе отсечения струи поле скоростей потока характеризуется значительной неравновесностью и он обладает кинетической энергией, превосходящей энергию стабилизированного потока с таким же расходом и равномерным полем скоростей.
Впроточной части камеры смешения имеют место: потери энергии, которые связаны с самим процессом смешения и являются потерями на удар; потери на трение; потери при истечении газа из сопла.
Основное назначение диффузора – увеличить избыточное давление, создаваемое эжектором. При выходе из него поток газовоздушной смеси обладает статическим давлением рСМ и скоростью WД . КПД диффузора снижается с увеличением неравномерности входного поля скоростей. Если в камере смешения газовоздушная смесь не дос-
110
таточно хорошо перемешалась, то она закончится в диффузоре, что обеспечит равномерное поле концентраций смеси.
Расчет эжектора базируется на законах количества движения (импульсов), сохранения энергии и неразрывности (сохранения массы) [8, 9].
Закон количества движения для сечений 1 и 2 эжектора, представленного на рис. 59, может быть представлен так:
|
|
WCM1 WГ M3 FГ ( рСМ |
рТР рД ), |
(11) |
где M1 и M3 – массовые расходы газа и газовоздушной смеси; |
||||
|
WC |
– средняя скорость истечения газа из сопла; |
||
рД |
WГ |
– скорость газовоздушной смеси в горле эжектора; |
||
и рСМ – статическое давление, |
создаваемое |
диффузором и |
||
|
рТР |
эжектором; |
|
|
|
– потери давления на трение в камере смешения; |
|||
|
FГ |
– поперечное сечение горла эжектора. |
|
|
При низком давлении можно пренебречь сжимаемостью газа и на основании закона сохранения массы можно написать следующие уравнения:
M1 V1 Г |
WC FC Г ; |
(12) |
||||
M3 V3 СМ |
WГ FГ СМ ; |
(13) |
||||
V3 V1 V2; |
M3 M1 |
M2; |
(14) |
|||
CM |
M |
Г |
1 u |
, |
|
|
3 |
|
|
(15) |
|||
V |
1 us |
|||||
3 |
|
|
|
|
|
|
где V1, V2 и V3 – объемные расходы газа, воздуха и газовоздушной смеси;
М2 – массовый расход воздуха; FC – выходное сечение сопла;
Г, В, СМ – плотности газа, воздуха и газовоздушной смеси; s = Г / В – относительная плотность газа;
u |
M2 |
, |
(16) |
|
M1 |
||||
|
|
|
111

где u – массовый коэффициент эжекции; us – объемный коэффициент эжекции
us |
V2 |
a'V0; |
1 us |
V3 |
. |
(17) |
||
|
||||||||
V1 |
||||||||
|
||||||||
|
|
|
|
V1 |
|
|||
Обозначим |
|
FГ |
|
|
|
|
||
|
|
F |
. |
(18) |
||||
|
|
|
||||||
|
|
|
FС |
|
||||
Эта величина является основным параметром эжектора. Подставляем полученные зависимости в выражение (11):
2W |
2 |
|
|
|
1 u 1 us |
рСМ |
рТР рД , |
|
|||
|
|
C |
|
Г 1 |
1Г |
|
|
(19) |
|||
|
|
F |
|||||||||
F 2 |
|
|
|
|
|
|
|
|
|||
где 1Г – коэффициент, учитывающий неравномерность скоростного поля в горле.
Потери давления на трение определяются уравнением
|
|
|
рТР |
|
W2 |
|
|
|
|
|
T |
Г |
CM , |
(20) |
|
|
lK |
2 |
|||||
|
|
|
|
|
|
||
где T |
|
– коэффициент сопротивления трения; |
|
||||
|
|
||||||
|
|
dK |
|
|
|
|
|
– коэффициент трения;
lК – длина камеры смешения;
dГ – диаметр горловины эжектора.
Закон сохранения энергии дает следующие зависимости: для сопла
р 2 WС2 ;
ГАЗ С 2 Г
для диффузора
рД W2Г2 СМ n2n2 1 Д ,
(21)
(22)
где рГАЗ – располагаемое (избыточное) давление газа перед соплом;С – коэффициент расхода сопла;
112

FД
n – степень расширения диффузора;
FГ
FД – выходное сечение диффузора;
Д – коэффициент сопротивления диффузора, отражающий потери энергии с учетом коэффициента неравномерности поля скоростей; Д отнесен к большей скорости.
После преобразования уравнение (19) примет вид
|
p |
2 |
2 |
|
|
2k |
1 u 1 us , |
|
|||||
|
CM |
|
|
С |
|
|
C |
(23) |
|||||
|
|
F |
|
|
2 |
||||||||
|
pГАЗ |
|
|
|
F |
|
|
|
|
|
|
||
где |
|
|
|
|
|
|
|
|
|
|
|
||
|
k 2 |
|
|
|
|
|
|
|
n2 |
1 |
|
||
|
1Г Т |
|
Д |
|
|
|
. |
(24) |
|||||
|
n |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение (23) является основным уравнением для расчета эжектора и его характеристикой. Оно связывает безразмерное давление,
создаваемое эжектором |
pCM |
, с коэффициентом эжекции |
u |
M2 |
и |
|
|||||
|
M1 |
||||
|
pГАЗ |
|
|
||
основным параметром эжектора F FГ .
FС
Характеристическое уравнение (23) выведено из схемы давлений, представленной на рис. 59. Схема предполагает режим работы эжектора, при котором давление в пределах конической части камеры смешения поддерживается постоянным и повышается в цилиндрической части.
Оптимальное значение основного параметра эжектора определяется из характеристического уравнения (23) путем его дифференцирования и отыскания максимума
|
|
рСМ |
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|||
|
|
|
|
|
|
|||
|
|
рГАЗ |
|
2μС |
|
2FμCk |
(1 u)(1 us) 0. |
|
|
|
dF |
|
F2 |
F4 |
|||
|
|
|
|
|
|
|||
Отсюда
FОПТ k 1 u 1 us . |
(25) |
113

Максимальное безразмерное давление, создаваемое эжектором, определяется выражением
|
ΔpCM |
|
|
2 |
|
|
|
|
С |
|
|
||||
|
|
|
. |
(26) |
|||
|
Δp |
|
|
F |
|||
|
|
ГАЗ max |
|
ОПТ |
|
|
|
Анализ последнего уравнения показывает, что с увеличением ко-
эффициента эжекции u безразмерное давление pCM будет умень-
pГАЗ
шаться. С увеличением плотности газа при одинаковых u pCM так-
pГАЗ
же будет уменьшаться.
На давление рСМ , создаваемое эжектором, значительное влияние оказывает профиль его проточной части. Чем рациональнее формы сопла и эжекционной трубки, тем выше эффективность эжектора. На величину минимально необходимого давления газа рГАЗ в значительной мере влияет форма сопла, так как при истечении из него поток газа обладает большой энергией, и каждый процент потери ее имеет существенное значение.
Коэффициент расхода С сопла в основном зависит от их конструкции и находится в пределах 0,84–0,97.
Профиль всасывающей камеры смешения выполняется конфузорным с поперечными сечениями, чтобы не стеснять развитие свободной струи газа, вытекающей из сопла. К наружной форме сопла особых требований не предъявляется, так как скорость потока воздуха мала.
Длина камеры смешения принимается такой, чтобы процесс стабилизации поля скоростей заканчивался до входа в диффузор. Обычно длину камеры принимают равной пяти диаметрам. Потери энергии на трение в камере смешения зависят от режима движения, качества обработки и длины. Для большинства горелок коэффициент потерьТ = 0,06–0,12. Значение коэффициента неравномерности скоростного поля в конце камеры смешения (в горловине) 1Г зависит от степени стабилизации потока и режима движения. При длине камеры смешения, равной 5–6 диаметрам, коэффициент 1Г = 1,02–1,04. Для укороченных камер 1Г принимает большее значение.
114
|
Плавное сопряжение |
|
||
2,2dГ |
|
с |
R = 1,7dГ |
|
|
|
|
|
|
dС |
|
|
dГ |
1,5dГ |
|
|
|
|
|
1,2dГ |
1,3dГ |
2,5dГ |
3,50 |
|
|
||||
|
5dГ |
|
|
4dГ |
|
|
|
9dГ |
|
dС
2,2dГ
0,6dГ
dС
2,2dГ
0,2dГ
а)
Плавное сопряжение  с R = 4,3dГ
с R = 4,3dГ
dГ 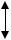


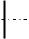



 1,4dГ
1,4dГ
|
3,50 |
|
2,2dГ |
3,5dГ |
|
|
||
6,3dГ
б)
Плавное сопряжение  с R = 2,4dГ
с R = 2,4dГ
dГ 







 1,4dГ
1,4dГ
|
3,50 |
|
1,6dГ |
3,8dГ |
|
|
||
5,6dГ
в)
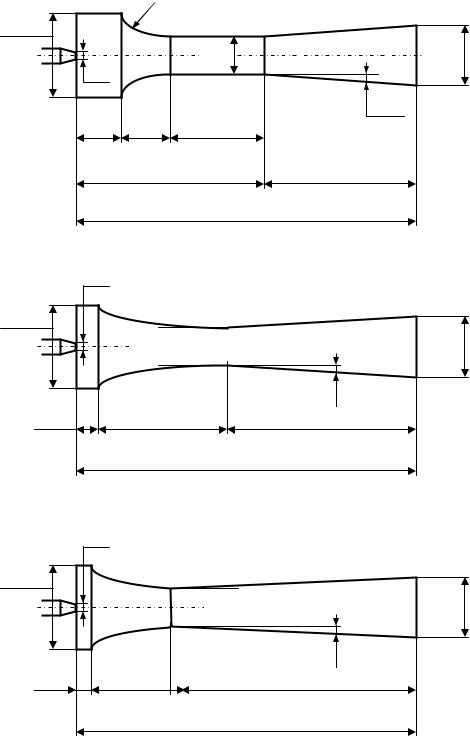
Рис. 61. Эжекционные трубки эжекторов с малой скоростью эжекции: а – оптимальная форма трубки, k = 1,5; б – укороченная трубка, k = 2,1; в – укороченная трубка, k = 3
115
Потери энергии в диффузоре зависят от степени расширения
|
F |
Д |
|
d |
Д |
2 |
|
|
n |
|
|
|
|
|
, угла раскрытия и коэффициента неравномерности |
||
F |
|
|
||||||
d |
|
|
||||||
|
|
Г |
|
|
Г |
|
||
входного поля скоростей. Оптимальный угол раскрытия диффузора составляет 2–80. Принимать степень расширения диффузора n > 3 нецелесообразно, так как большие n значительно увеличивают длину диффузора и лишь незначительно повышают статическое давление.
На рис. 61 показаны три варианта конструкций эжекционных трубок эжекторов с малой скоростью эжекции. Вариант а соответствует оптимальной форме проточной части. Гидравлические потери здесь будут наименьшими (коэффициент потерь k = 1,5).
В случае, когда избыточное давление газа в сети больше минимально необходимого, используют укороченные эжекционные трубки (см. рис. 61, б и в). Эти трубки характеризуются повышенными потерями энергии, но имеют меньшие линейные размеры. Для трубки типа б коэффициент k = 2,1, а для трубки типа в k = 3. Вопрос применения этих трубок зависит от располагаемого давления газа. Чем оно больше, тем более короткие трубки можно использовать.
5.3. Конструктивный расчет горелки
Основное уравнение горелки получают из сравнения характеристики эжектора (23), характеристик головки горелки (6), с учетом уравнений (12), (15), (17) и (21):
1 u 1 us |
2F |
|
, |
(27) |
k k F2 |
||||
1 |
1 |
|
|
|
где F1 = FГ / F0 , F = FГ / FС – параметры горелки; F0 – суммарная площадь выходных отверстий головки горелки.
Анализ уравнения (27) показывает, что эжекционная способность горелки зависит только от конструкции горелки и не зависит от режима ее работы. Следовательно, горелка обладает саморегулируемостью. Это положение подтверждается экспериментально для основного диапазона изменения нагрузок.
Оптимальное значение параметра горелки F1 получаем из уравнения (27) после подстановки в него выражения для FОПТ (25)
116

F1ОПТ |
k |
|
|
|
. |
(28) |
|
k |
|||
|
1 |
|
|
Для решения основного уравнения горелки (27) преобразуем его с учетом уравнения (28) и зависимости
|
x |
F1 |
. |
|
(29) |
|
|||||
|
|
F1ОПТ |
|
||
В результате преобразований получаем |
|
||||
|
Ax2 2x A 0, |
(30) |
|||
где |
|
||||
A |
k1 1 u 1 us F1ОПТ FС |
. |
(31) |
||
|
|||||
|
|
F0 |
|
||
Решая уравнение (30), получаем два значения для x. В качестве расчетного следует принимать меньшее значение. При А = 1 из (30) получаем x = 1, что соответствует оптимальному режиму работы горелки в соответствии с (29).
Если A > 1, уравнение (30) дает мнимые корни. Физически это означает, что горелка не может обеспечить требуемую эжекционную способность.
Если A < 1, то это значит, что имеет место избыточное давление газа и для сокращения размеров горелки целесообразно за расчетный режим принять неоптимальный режим или применять укороченную эжекционную трубку.
Выходное сечение сопла определяем из уравнений (12) и (21):
FC |
V1 |
Г |
|
. |
(32) |
С |
|
|
|||
|
|||||
|
2 ГАЗ |
|
|||
Рекомендуемый порядок конструктивного расчета атмосферной горелки:
–рассчитывают головку горелки и определяют a', u, d0 , F0 , k1 ;
–по заданному давлению газа находят FС . Принимают определенный вид эжекционной трубки, рассчитывают А и х;
–определяют F1ОПТ, FГ и все размеры эжектора.
Пример. Рассчитать атмосферную горелку производительностью V1 = 10 м3/ч, в которой сжигают природный газ с теплотворной
117

способностью QНС = 35 200 кДж/м3, плотностью = 0,73 кг/м3, теоретически необходимое количество воздуха для горения V0 = 9,3 м3/м3, давление газа перед горелкой рГАЗ = 1,3 кПа [9].
Решение. Выбираем расчетные значения основных параметров горелки: коэффициент избытка первичного воздуха a' = 0,6; диаметр сопла d0 = 6 мм; скорость потока на выходе из горелки W0 = 1,65 м/с. Принятая скорость позволяет работать горелке с перегрузкой до 2,95/1,65 = 1,79 раза (см. табл. 8). При a' = 0,6 проскока пламени не будет. Следовательно, диапазон регулирования горелки составляет 0 – 1,79 номинальной нагрузки. Глубину выходных каналов принимаем 12 мм.
1.Рассчитываем суммарную площадь выходных отверстий по формуле (5):
F0 V1 1 a'V0 10 1 0,6 9,3 111 см2.
W0 0,36 1,65
2. Рассчитываем коэффициент эжекции по формуле (17):
u a'V0 0,6 9,3 9,8. s 0,57
Здесь s ρГ 0,73 0,57 относительная плотность газа.
ρВ 1,22
3. Определяем значения коэффициентов потерь. Принимаем эжекционную трубку типа в (рис. 61) k = 3. Для отверстий горелки принимаем 0 = 0,8, а температуру подогрева 100 0С. Коэффициенты 0 и k1 рассчитываем по следующим формулам:
|
|
|
|
1- 2 |
|
1 0,82 |
|
|
|
|
|||
|
|
|
0 |
|
|
0 |
|
|
0,56; |
||||
|
|
|
02 |
0,82 |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
k ζ |
|
2 |
Т |
|
1 0,56 2 |
373 |
|
-1 2,3. |
|||||
|
|
|
|
|
|||||||||
1 |
0 |
|
|
273 |
|
|
273 |
|
|||||
Коэффициент расхода сопла принимаем С = 0,9.
4. Рассчитываем площадь и диаметр сопла по формуле (32):
118

FC |
|
V1 |
ρГ |
|
|
10 |
0,73 |
|
0,52 cм |
2 |
; dC = 8,1 мм. |
|
|
|
|
|
|
|
|
|
|||||
μС |
2 рГАЗ |
0,36 0,9 |
|
|
||||||||
|
|
|
|
|
2 1300 |
|
|
|||||
5. Рассчитываем F1ОПТ по формуле (28):
F1ОПТ 
 k/k1
k/k1 
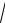 3/2,3 1,14.
3/2,3 1,14.
6.Рассчитываем А по формуле (31):
Аk1(1 u)(1 us)F1ОПТ FC 2,31 9,8 1 9,8 0,57 0,52 1,14 0,885.
F0 |
111 |
Так как А < 1, следовательно, давление газа рГАЗ = 1,3 кПа больше минимально необходимого. Для сокращения размеров горелки рассчитываем ее на неоптимальный режим. Определяем х по формуле
(30):
0,885 х2 – 2 х + 0,885 = 0; х = 0,6.
7. Определяем FГ по формуле (29):
F1 = x F1ОПТ = 0,6 1,14 = 0,685 см2;
FГ = F1 F0 = 0,685 111 = 76 см2; dГ = 9,8 мм.
Остальные размеры эжектора берем по рис. 61 как величины, кратные dГ .
5.4.Расчет параметров работы горелки
Впрактике часто возникает вопрос о работе горелки при изменении теплотворной способности топлива QНС, номинального давления
ссохранением производительности горелки (достигается изменением
диаметра сопла) и относительной плотности газа s = Г / В .
При сопоставлении уравнений (27) и (32) получим постоянную горелки С:
С |
2,48FГ μС |
|
V1(1 u)(1 us) s |
. |
(33) |
||
2 |
|
|
|
||||
|
|||||||
|
k k1F1 |
|
|
ΔpГАЗ |
|
||
119
