Тема 2 Наращение и дисконтирование с использованием схемы простых процентов

Основу коммерческих вычислений составляют ссудно-заемные операции, в которых и проявляется, прежде всего, необходимость учета временной стоимости денег.

Несмотря на то, что в основе расчетов заложены простейшие вычислительные схемы, эти расчеты весьма многообразны, так как предусматривают различные условия контрактов, частоту и способы начислений, различные варианты предоставления и погашения ссуд.

Рассмотрев операции наращения, можно увидеть, что, предоставляя свои денежные средства в долг, их владелец получает определенный доход в виде процентов в течение определенного промежутка времени. Поскольку стандартным временным интервалом в финансовых операциях является год, наиболее распространен вариант, когда процентная ставка устанавливается в виде годовой ставки, под­разумевающей однократное начисление процентов по истечении года после получения ссуды. Известны две основные схемы дискретного начисления:

1) схема простых процентов;

2) схема сложных процентов.

По отношению к моменту времени начисления или выплаты проценты делятся на обычные и авансовые.

Обычные(заемные, декурсивные, postnumerando)проценты начисляются в конце периода финансовой операции.

Авансовые (антисипативные, дисконтные, учетные, prenumerando) начисляются в начале периода.

Схема простых процентов предполагает неизменность базы, с которой происходит начисление. Если исходный инвестируемый ка­питал равенPV, а требуемая доходность в долях единицы составляетr, то считается, что инвестиция сделана на условиях простого про­цента, если инвестированный капитал ежегодно увеличивается на ве­личинуPV r.

Таким образом, через nлет размер инвестированного капитала будет равен:

FV = PV + PV*r + … + PV*r = PV + PV*n*r = PV*(1 +n* r)

Из приведенной формулы видно, что проценты начисляются на одну и ту же величину капитала в течение всего срока. Это выражение называется формулой наращения простыми процентами, а множитель (1 + n*r) – множителем наращения или коэффициентом наращения простыми процентами.

Из приведенной формулы видно, что приращение капитала со­ставляет величину PV*n*r, оно пропорционально сроку ссуды и ставке процента и растет линейно вместе с ростомn.Величину PV*n*rчасто называютпроцентным платежом.

Необходимо обратить внимание на размерность величин, опре­деляющих размер процентного платежа. Размерностиnиrвсегда должны быть согласованы. Таким образом, либоnдолжно измеряться в годах, либо с изменением размерностиn(например, не годы, а кварталы) ставка процента должна отра­жать рост за новую единицу времени (за квартал).

Исходя из сказанного наращение по простым процентам в слу­чае, если продолжительность финансовой операции не равна целому числу лет (например, меньше года), определяется по формуле:

где t – продолжительность финансовой операции в днях;

Т- количество дней в году.

Наращение по простым процентам применяется при обслужива­нии депозитных вкладов с ежемесячной выплатой процентов, и вообще в тех случаях, когда проценты не присоединяются к сумме долга, а периодически выплачиваются вкладчику. Простые проценты применяют и при выдаче широко распространенных краткосрочных ссуд, т.е. ссуд, предоставляемых на срок до одного года с однократ­ным начислением процентов.

При использовании схемы простых процентов частота начисле­ния не оказывает никакого влияния на суммарную величину процент­ных денег.

Пример

Клиент поместил в банк вклад в сумме 35 тыс. руб. под 15 % го­довых.

Какова будет суммарная величина процентных денег, если:

а) проценты будут начисляться один раз в конце года;

б) проценты будут начисляться ежемесячно?

В первом случае FV – PV= 35* 0,15* 1 год = 5,25 тыс. руб.

Во втором случае FV – PV= 35* 1/12* 0,15 = 437,5 руб.

Т.е. во втором случае суммарный годовой доход клиента в виде на­численных процентов составит те же 437,5* 12 = 5,25 тыс. руб.

При определении продолжительности финансовой опера­ции принято день выдачи и день погашения ссуды считать одним днем. В зависимости от того, чему принимается равной продолжи­тельность периода сделки (год, квартал, месяц), размер промежу­точной процентной ставки может быть различным. Возможны сле­дующие варианты:

1) точный процент (exactinterest), определяемый исходя из точного числа дней в году (365 или 366), в квартале (от 89 до 92), в месяце (от 28 до 31);

2) обыкновенный процент (ordinaryinterest), определяемый исходя из прибли­женного числа дней в году, квартале, месяце (соответственно, 360, 90, 30).

При определении продолжительности периода, на который вы­дана ссуда, также возможны два варианта:

1) в расчет принимается точное число дней, на которое вы­дана ссуда;

2) в расчет принимается приближенное число дней, не кото­рое выдана ссуда (исходя из продолжительности месяца 30 дней).

Исходя из сказанного, расчет может выполняться одним из трех способов:

1) Точный процент с точным числом дней. Этот вариант дает самые точные результаты (Вели­кобритания, США). Обозначение 365/365, ACT/ACT.

2) Обыкновенный процент с точным числом дней. Этот метод иногда называют банковским (Banker’sRule), распространен в ссудных операциях коммерческих банков, в частности во Франции, Бельгии.Этот вариант дает несколько больший результат, чем применение точных процентов. При числе дней ссуды, превышающем 360, данный способ приводит к тому, что сумма начисленных процентов будет больше, чем предусматривается годовой ставкой. Например, если t=364, то n=364/360=1,011. Обычно это условие финансовой сделки обозначается как 365/360,ACT/360.

3) Обыкновенный процент с приближенным чис­лом дней. Такой метод применяется тогда, когда не требуется большой точности, например при промежуточных расчетах. Он принят в коммерческих банках Германии. Обозначение в условиях фи­нансовой сделки 360/360, или немецкая практика;

Вариант с точными процентами и приближенным числом дней ссуды лишен смысла и не применяется.

Величина эффекта от выбора того или иного способа зависит от размеров суммы, фигурирующей в процессе финансовой операции.

Пример. Банк выдал кредит 20.01. в размере 500 тыс. руб. Срок возврата кредита 05.10. Процентная ставка установлена в размере 15% годовых. Год не високосный.

Точное число дней (по таблице) = 278 - 20 = 258 дня.

Приближенное число дней = 12 дней января + 30 дней февраля + 30 дней марта + 30 дней апреля + 30 дней мая + 30 дней июня + 30 дней июля + 30 дней августа + 30 дней сентября + 5 дней октября – 1 день = 256 дней.

 точный процент и точное число дней

тыс. руб.

 обыкновенный процент и точное число дней

тыс. руб.

 обыкновенный процент и приближенное число дней

тыс. руб.

Между величинами процентного дохода, рассчитанными с использованием различной временной базы, при равной продолжительности ссуды существуют следующие соотношения:

Эти соотношения могут быть использованы при определении эквивалентных процентных ставок, то есть ставок, приносящих одинаковые процентные доходы при различных временных базах, но равных первоначальных капиталах:

В мировой практике при расчете процента используют и другие величины.

Пусть 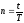. Тогда в формуле процентных денегможно записать. Поделив числитель и знаменатель дроби правой части равенства наr, получим:

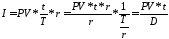, где.

В этих формулах – т.н. процентное число;

– процентный ключ или дивизор.

Естественно, что при одной и той же ставке , но при различных значениях(360 или 365 дней) будет разным и дивизор.

Дивизор численно равен такому количеству денежных единиц, с которого при ставке процента получается 1 денежная единица в день.

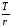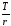Если PV=руб. (приt=T), тоI = **r = t (руб.в день).

Пример. Вычислить процент с капитала в 2,4 млн. руб., отдан­ного в долг по ставке 16% годовых на срок с 05.03. по 21.09. того же года, если расчет ведется способом 365/365.

t= 264 –64 = 200 дней.

D= 365/0,16 = 2281,25

I= 2,4*200/2281,25= 0,210411млн. руб.

Проверим: FV= 2281.25*(1 + 200/365*0,16) = 2481.25 руб.

Доход от операции 2481.25 – 2281.25 = 200 руб. за 200 дней или 1 руб. дохода за день финансовой операции (что и требовалось доказать).