Математическое обеспечение

фининсовых

решений

Тема 1

Временная стоимость денег.

Операции наращения и дисконтирования

В практических финансовых операциях суммы денег вне зависимости от их назначения или происхождения, так или иначе, но обязательно связываются с конкретными моментами или периодами времени. Для этого в контрактах фиксируются соответствующие сроки, даты, периодичность выплат. Фактор времени, особенно в долгосрочных операциях, играет не меньшую, а иногда даже большую роль, чем размеры денежных сумм. Необходимость учета временного фактора вытекает из сущности финансирования и кредитования и выражается в принципе неравноценности денег, относящихся к разным моментам времени(или стоимость денег во времени –timevalueofmoney). Очевидно, что 100 000 руб., полученных через 5 лет, не равноценны этой же сумме поступившей сегодня.

Временная стоимость денег обуславливается наличием двух причин:

1) обесценением денежной наличности с течением времени. Так, если предприятие имеет свободные денежные средства в раз­мере 10,0 млн. руб., а инфляция, то есть обесценение денег, состав­ляет 20% в год, то это означает, что уже через год, в случае если предприятие никак их не инвестирует, они уменьшатся по своей покупательной способности и составят в текущих ценах только 8 млн. руб.;

2) обращением капитала (денежных средств). Предположим, что предприятие имеет возможность участвовать в инвестиционном проекте, который может принести доход в размере 20,0 тыс. руб. по истечении двух лет. Имеется возможность выбора варианта получе­ния дохода: либо по 10 тыс. руб. по истечении каждого года, либо единовременное получение всей суммы в конце двухлетнего периода. Очевидно, что второй вариант получения доходов менее выгоден по сравнению с первым, так как сумма, полученная в конце первого года, может принести дополнительные доходы.

(В Индии, на химическом заводе американской компании, произошла крупная авария. В качестве компенсации пострадавшим первоначально предложили выплатить 200 млн. долл. в течение 35 лет. Предложение было отклонено. Для иллюстрации влияния фактора времени скажем, что 57,6 млн. долл. в банк под 10% годовых обеспечит последовательную выплату 200 млн. долл. Т.е. 57.6 млн. выплаченных сегодня равнозначны 200 млн. долл. погашаемым ежемесячно в равных долях)

Простейшим видом финансовой операции является однократ­ное предоставление в долг некоторой суммы PV(presentvalue) с условием, что через какое-то времяtбудет возвращена большая суммаFV(futurevalue).

Результативность подобной сделки может быть охарактеризо­вана двояко: либо с помощью абсолютного показателя либо путем расчета некоторого относительного показателя.

Абсолютным показателем является разность I=FV-PV, которая называется процентом (interest) или суммой процентных денег. Это величина дохода от предоставления в долг денежной суммы PV.

Однако для оценки эффективности финансовых операций абсолютные пока­затели мало применимы ввиду их несопоставимости. Поэтому пользуются специальным коэффициентом – став­кой.

Под процентной ставкой (rate of interest) – понимается относительная величина дохода за фиксированный отрезок времени, т.е. отношение дохода (процентных денег) к сумме долга за единицу времени.

Временной интервал, которому соответствует процентная ставка, называют периодом начисления(год, полугодие, квартал, месяц, даже день).

Размер процентной ставки зависит от ряда объективных и субъективных факторов: общего состояния экономики, в том числе денежно кредитного рынка, кратковременных и долгосрочных ожиданий его динамики, вида сделки, ее валюты, срока кредита и т.д.

В общем виде процентная ставка может быть представлена как сумма четырех основных компонент, определяющих величину r:

r = i + f + E + g

где i – норма процента, отражающая компенсацию кредитору за от­каз использовать в других целях предоставленную сумму в течение времениt (пока не вернут долг);

f – так называемый фактор риска (эффект Фишера), представ­ляющий собой для кредитора компенсацию за неопределенность (риск) неполучения процентов или всей суммы вообще при наступле­нии срока возврата долга;

Е– инфляционная добавка, т.е. компенсация за возможное из­менение в уровне цен, за уменьшение покупательной способности де­нег вследствие инфляции;

g – компенсация, зависящая от продолжительности срока, на который ссужены деньги, и тем большая, чем длительнее этот срок.

В финансовом анализе процентная ставка применяется не только как инструмент наращения суммы долга, но и в более широком смысле – как измеритель степени доходности (эффективности) любой финансовой операции), независимо от того имел место или нет факт выдачи денег в долг и процесс наращения этой суммы.

Существует два принципа расчета процентов – наращение на сумму долга и скидка с конечной суммы задолженности. Соответственно применяют ставку наращения (interest base rate) и учетную ставку (discount base rate). Оба вида ставок применяются для решения сходных задач. Однако для ставки наращения прямой задачей является определение наращенной суммы, обратной дисконтирование. Для учетной ставки наоборот, прямая задача заключается в дисконтировании, обратная - в наращении.

Для расчета процентной ставки используется сле­дующая формула:

, (1)

Для расчета учетной ставки используется сле­дующая формула:

. (2)

Оба вышеназванных показателя взаимосвязаны между собой, т.е. зная один показатель можно рассчитать и другой:

(3) или. (4)

Оба показателя могут выражаться либо в десятичных дробях, либо в процентах.

Из определения показателей следует, что r › 0и 0 ‹ d ‹ 1. Слу­чай, когдаr = 0иd = 0, не рассматривается, так как тогдаFV = PV, т.е. можно считать, что финансовой сделки как таковой просто нет. Случай, когдаd = 1соответствует PV = 0 , т.е. не предоставляется ни­какая сумма в долг, а через некоторое время получаем FV.

Степень расхождения между d(t) иr(t) зависит от уровня процентных ставок, имеющих место в конкретный момент времени. Так, еслиr = 7%, тоd = 6,54, т.е. расхождение сравнительно невелико. Однако, еслиr = 70%, тоd = 41,18%,т.е. ставки существенно различаются по величине.

В прогнозных расчетах, например, при оценке инвестиционных проектов, как правило, имеют дело с процентной ставкой. Учетная ставка в основном используется в банковских операциях по учету векселей.

Процесс, в котором заданы исходная сумма и процентная ставка, в финансовых вычислениях называется процессом нараще­ния (компаундинг). Причем величинаFVпоказывает будущую стоимость «сего­дняшней» величиныPVпри заданном уровне доходности.

Процесс, в котором заданы ожидаемая в будущем к получению (или возвращаемая) сумма и коэффициент дисконтирования, называ­ется процессом дисконтирования. Экономический смысл дисконтирования заключается во вре­менном упорядочении денежных потоков различных временных пе­риодов. При этом случае искомая величинаPV показывает текущую, «сегодняшнюю» стоимость будущей величиныFV.

В первом случае речь идет о движении денежного потока от на­стоящего к будущему, а во втором – о движении от будущего к на­стоящему.

Логика финансовых операций представлена на рис. 1.

Настоящее Будущее

Исходная сумма

Наращение Возвращаемая сумма

Процентная ставка

Ожидаемая к поступлению сумма

Приведенная сумма Дисконтирование

Коэффициент дисконти­рования

Рис. 1. Логика финансовых операций

Экономический смысл финансовой операции, которая пред­ставляется формулой (1), состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции. Поскольку из формулы (1) следует, что FV = PV * (1 + r_t ), то FV › PV(так как (1 +r_t) › 1), т.е. время генерирует деньги.

Естественно, такой же вывод можно сделать, используя фор­мулу (2), так как из нее следует, что PV = FV*(1 – d_t ), и справедливо нера­венство1 – d ‹ 1.

Как уже отмечалось выше, в качестве ставки наращения может вы­ступать как процентная, так и учетная ставка. Если наращенная сумма находится по формуле FV = PV*(1 + r_t ), то ставкой наращения является процентная ставка. С другой стороны, из формулыPV = FV*(1 – d)следует, что наращен­ную сумму можно определять по формуле:

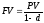
Поэтому в этом случае ставкой наращения является учетная ставка. Учетная ставка используется для наращения в случае учета векселя в банке, если рассматривать эту операцию с позиции банка.

Аналогичные рассуждения можно высказать и в связи с процессом дисконтирования. Если приведенная сумма находится по формуле PV = FV*(1 – d), то в качестве ставки приведения выступает учетная ставка. С дру­гой стороны, из формулыFV= PV*(1 + r)следует, что приведенную сумму можно определить также по формуле.В этом случае в качестве ставки дисконтирования выступает процентная ставка.